2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件6新人教B版选修2_1(30张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件6新人教B版选修2_1(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 14:52:40 | ||
图片预览










文档简介
课件30张PPT。【课标要求】
空间向量与空间角【核心扫描】
理解直线与平面所成角的概念.
能够利用向量方法解决线线、线面、面面的夹角问题.
体会用空间向量解决立体几何问题的三步曲.
向量法求解线线、线面、面面的夹角.(重点)
线线、线面、面面的夹角与向量的应用.(难点)
1.2.3.1.2.想一想:当一条直线l与一个平面α的夹角为0时,这条直线一定在平面内吗?
提示 不一定,这条直线还可能与平面平行.
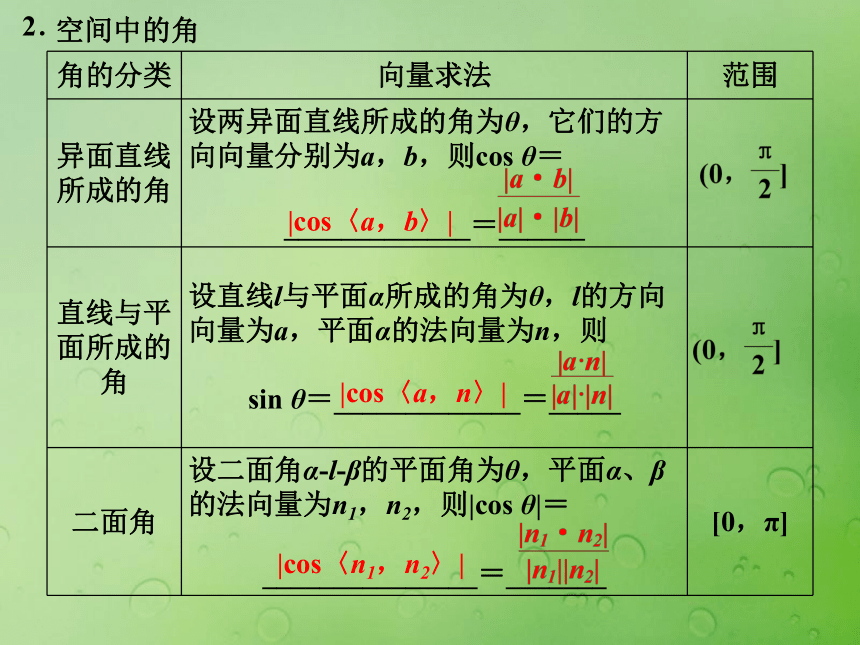
自学导引投影夹角0空间中的角
|cos〈a,b〉|2.|cos〈a,n〉||cos〈n1,n2〉|试一试:若二面角α -l -β的两个半平面的法向量分别为n1,n2,试判断二面角的平面角与两法向量夹角〈n1,n2〉的关系.
提示 相等或互补
两异面直线所成角的求法
(1)平移法:即通过平移其中一条(也可两条同时平移),使它们转化为两条相交直线,然后通过解三角形获解.
名师点睛1.直线与平面所成角的求法
(1)几何法:找出斜线在平面上的射影,则斜线与射影所成角就是线面角,可通过解由斜线段、垂线段和射影线段构成的直角三角形获解.
2.二面角的求法
(1)几何法:作出二面角的平面角,然后通过解三角形获解.
(2)向量法:设二面角α -l-β的两个半平面的法向量分别为n1,n2.
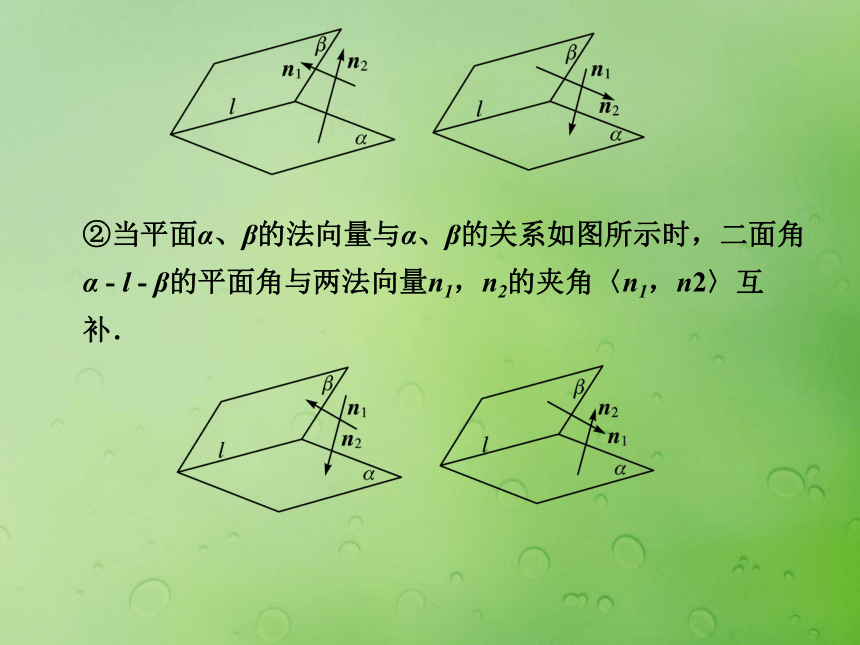
①当平面α、β的法向量与α、β的关系如图所示时,二面角α - l - β的平面角即为两法向量n1,n2的夹角〈n1,n2〉.
3.②当平面α、β的法向量与α、β的关系如图所示时,二面角α - l - β的平面角与两法向量n1,n2的夹角〈n1,n2〉互补.
题型一 求异面直线的夹角 正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求异面直线AE与CF所成角的余弦值.
【例1】解 不妨设正方体棱长为2,分别取DA、DC、DD1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则
规律方法 在解决立体几何中两异面直线所成角问题时,若能构建空间直角坐标系,则建立空间直角坐标系,利用向量法求解.但应用向量法时一定要注意向量所成的角与异面直线所成角的区别.
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角的余弦值.
【变式1】解 (1)如图,建立空间直角坐标系.
∵∠ADC=∠DAB=90°,
AB=4,CD=1,AD=2.
∴A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得
[思路探索] 利用正三棱柱的性质,建立适当的空间直角坐标系,写出有关点的坐标.求角时有两种思路:一是由定义找出线面角,取A1B1的中点M,连结C1M,证明∠C1AM是AC1与平面A1ABB1所成的角;另一种是利用平面A1ABB1的法向量n=(λ,x,y)求解.
题型二 求线面角【例2】规律方法 用向量法求线面角的一般步骤是:先利用图形的几何特征建立适当的空间直角坐标系,再用向量有关知识求解线面角.法二给出了用向量法求线面角的常用方法,即先求平面法向量与斜线夹角,再进行换算.
【变式2】 (12分)如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点,求二面角A-A1D-B的余弦值.
题型三 二面角的求法【例3】[规范解答]如图所示,取BC中点O,连结AO.因为△ABC是正三角形,所以AO⊥BC,因为在正三棱柱ABC — A1B1C1中,平面ABC⊥平面BCC1B1,所以AO⊥平面BCC1B1.
【题后反思】 几何法求二面角,往往需要作出其平面角,这是该方法的一大难点.而用向量法求解二面角,无需作出二面角的平面角,只需求出平面的法向量,转化为两直线(或两向量)所成的角,通过向量的数量积运算即可获解,体现了空间向量的巨大优越性.
【变式3】 空间向量的具体应用主要体现为两种方法——向量法和坐标法.这两种方法的思想都是利用空间向量表示立体图形中的点、线、面等元素,建立立体图形和空间向量之间的联系,然后进行空间向量的运算,最后把运算结果回归到几何结论.这样就把立体几何问题转化为空间向量来研究,体现了化归与转化思想.
方法技巧 化归与转化思想解决立体几何问题(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小.
[思路分析]建系→求相关点坐标→求相关向量坐标→向量运算→结论.
解 作AP⊥CD于点P,分别以AB,AP,AO所在的直线为x,y,z轴建立空间直角坐标系A-xyz,如图所示,
【示例】
空间向量与空间角【核心扫描】
理解直线与平面所成角的概念.
能够利用向量方法解决线线、线面、面面的夹角问题.
体会用空间向量解决立体几何问题的三步曲.
向量法求解线线、线面、面面的夹角.(重点)
线线、线面、面面的夹角与向量的应用.(难点)
1.2.3.1.2.想一想:当一条直线l与一个平面α的夹角为0时,这条直线一定在平面内吗?
提示 不一定,这条直线还可能与平面平行.
自学导引投影夹角0空间中的角
|cos〈a,b〉|2.|cos〈a,n〉||cos〈n1,n2〉|试一试:若二面角α -l -β的两个半平面的法向量分别为n1,n2,试判断二面角的平面角与两法向量夹角〈n1,n2〉的关系.
提示 相等或互补
两异面直线所成角的求法
(1)平移法:即通过平移其中一条(也可两条同时平移),使它们转化为两条相交直线,然后通过解三角形获解.
名师点睛1.直线与平面所成角的求法
(1)几何法:找出斜线在平面上的射影,则斜线与射影所成角就是线面角,可通过解由斜线段、垂线段和射影线段构成的直角三角形获解.
2.二面角的求法
(1)几何法:作出二面角的平面角,然后通过解三角形获解.
(2)向量法:设二面角α -l-β的两个半平面的法向量分别为n1,n2.
①当平面α、β的法向量与α、β的关系如图所示时,二面角α - l - β的平面角即为两法向量n1,n2的夹角〈n1,n2〉.
3.②当平面α、β的法向量与α、β的关系如图所示时,二面角α - l - β的平面角与两法向量n1,n2的夹角〈n1,n2〉互补.
题型一 求异面直线的夹角 正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求异面直线AE与CF所成角的余弦值.
【例1】解 不妨设正方体棱长为2,分别取DA、DC、DD1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则
规律方法 在解决立体几何中两异面直线所成角问题时,若能构建空间直角坐标系,则建立空间直角坐标系,利用向量法求解.但应用向量法时一定要注意向量所成的角与异面直线所成角的区别.
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠ADC=∠DAB=90°,AB=4,CD=1,AD=2.
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角的余弦值.
【变式1】解 (1)如图,建立空间直角坐标系.
∵∠ADC=∠DAB=90°,
AB=4,CD=1,AD=2.
∴A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得
[思路探索] 利用正三棱柱的性质,建立适当的空间直角坐标系,写出有关点的坐标.求角时有两种思路:一是由定义找出线面角,取A1B1的中点M,连结C1M,证明∠C1AM是AC1与平面A1ABB1所成的角;另一种是利用平面A1ABB1的法向量n=(λ,x,y)求解.
题型二 求线面角【例2】规律方法 用向量法求线面角的一般步骤是:先利用图形的几何特征建立适当的空间直角坐标系,再用向量有关知识求解线面角.法二给出了用向量法求线面角的常用方法,即先求平面法向量与斜线夹角,再进行换算.
【变式2】 (12分)如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点,求二面角A-A1D-B的余弦值.
题型三 二面角的求法【例3】[规范解答]如图所示,取BC中点O,连结AO.因为△ABC是正三角形,所以AO⊥BC,因为在正三棱柱ABC — A1B1C1中,平面ABC⊥平面BCC1B1,所以AO⊥平面BCC1B1.
【题后反思】 几何法求二面角,往往需要作出其平面角,这是该方法的一大难点.而用向量法求解二面角,无需作出二面角的平面角,只需求出平面的法向量,转化为两直线(或两向量)所成的角,通过向量的数量积运算即可获解,体现了空间向量的巨大优越性.
【变式3】 空间向量的具体应用主要体现为两种方法——向量法和坐标法.这两种方法的思想都是利用空间向量表示立体图形中的点、线、面等元素,建立立体图形和空间向量之间的联系,然后进行空间向量的运算,最后把运算结果回归到几何结论.这样就把立体几何问题转化为空间向量来研究,体现了化归与转化思想.
方法技巧 化归与转化思想解决立体几何问题(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小.
[思路分析]建系→求相关点坐标→求相关向量坐标→向量运算→结论.
解 作AP⊥CD于点P,分别以AB,AP,AO所在的直线为x,y,z轴建立空间直角坐标系A-xyz,如图所示,
【示例】
