2018年高中数学第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件7新人教B版选修2_1(28张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件7新人教B版选修2_1(28张) |  | |
| 格式 | zip | ||
| 文件大小 | 341.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 14:55:17 | ||
图片预览




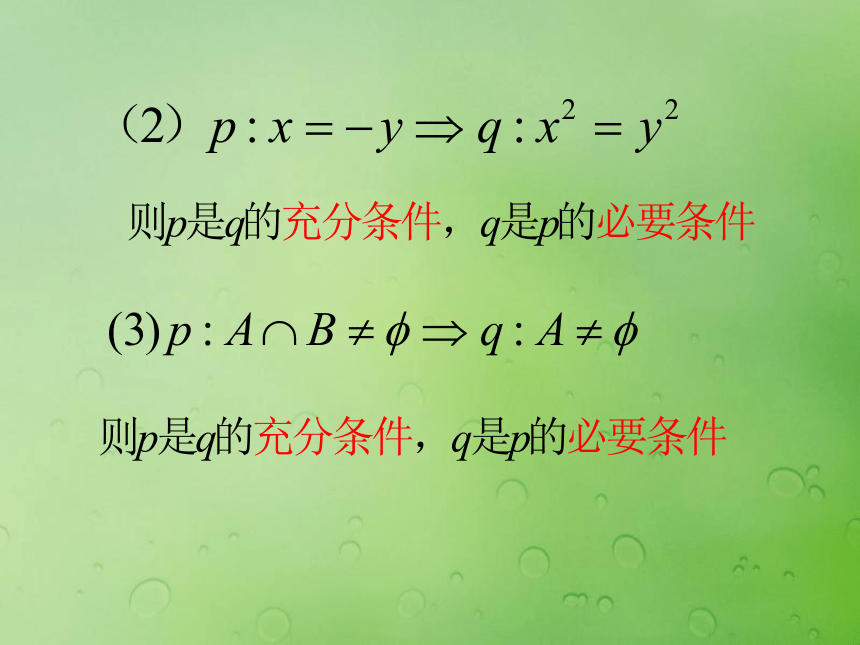




文档简介
课件28张PPT。推出与充分条件、必要条件做一做:判断下列“如果p,则q”形式命题的真假.(1)如果四边形是正方形,则它的四边
也相等.
(2)如果X2=Y2,则x=-y.
(3)如果a2+b2=0,则a=b=0.
(4)如果a=b=0,则a2+b2=0.
(5)如果A∩B≠φ,则A≠φ.
真假真真真二、新课讲授1、一般地:若p则q为真,记作: 或若p则q为假,记作:(1)如果两个三形全等,那么两三角形面积相等。
(2)“若 则 ”为假命题例如两个三形全等 两三角形面积相等二、新课讲授2、充分条件与必要条件一般地,如果已知 那么我们就说 p是q的充分条件, q是p的必要条件。(1).两个三角形全等 两三角形面积相等。“两个三角形全等”是“两三角形面积相等”的充分条件“两三角形面积相等”是“两个三角形全等 ”的必要条件例如3、充分不必要条件与必要不充分条件一般地,如果已知 且
那么我们就说: p是q的充分不必要条件, q是p的必要不充分条件(1).两个三角形全等 两三角形面积相等但:两三角形面积相等 两个三形全等“两个三角形全等”是“两三角形面积相等”的充分不必要条件“两三角形面积相等”是“两个三角形全等 ”的必要不充分条件4、充要条件一般地,如果已知
即: 那么我们就说: p是q的充要条件, q是p的充要条件例如充分不必要条件必要不充分条件既不充分也不必要条件充分且必要条件(3)“ a2>b2 ”是“ a>b ”的什么条件?(2)“四边形为平行四边形”是“这个四边形为菱形”的什么条件?利用定义解决问题,并寻找判断方法. 目的 pqppqq找p、q判断p q,与
q p的真假根据定义
下结论(1)“a>0,b>0”是“ab>0”的什么条件?(答:充分不必要条件)(答:必要不充分条件)(答:既不充分也不必要条件)例题1: 例题2:说出下列各组命题中,p是q的什么条件?q是p的什么条件? 所以:p是q的充分不必要条件,q是p的必要不充分条件.(2) p: (a-2)(a-3)=0, q: a=3 所以:p是q的必要不充分条件,q是p的充分不必要条件.所以:p与q互为充要条件(4)P: a < b . q: <1 ab所以:p是q的既不充分也不必要的条件
q是p的既不充分也不必要的条件例题3:若A是B 的充要条件,B是C 和D 的必要条件,E是D 的充分条件,E 是A 的充要条件,
则E是B的_______条件,
C是A的________条件,
A是D的________条件,
D是C的_________条件.A BC
DEE BC AA DC D充要条件充分不必要充要条件必要不充分1、已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要条件2.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件练习1.已知p:{x|0 则p是q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件 2、已知p:|x+1|>2,q:x2<5x-6,
则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件例5、AA3:填写“充分不必要,必要不充分,充要,既不充分又不必要。
1)sinA>sinB是A>B的_________ 条件。
2)在ΔABC中,sinA>sinB是 A>B的________条件。既不充分又不必要充要条件4、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc2D4、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.02},N={x|x<3}, 那么”x∈M或x∈N”是“x∈M∩N”的( )
A.充要条件 B必要不充分条件 C充分不必要 D不充分不必要B1.已知 是实数,则“ 且 ”是“ 且 ”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件 2.“ ”是“ ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件 AC【第二组题】
(1) 的(充分不必要)条件。
(2)“四边形为平行四边形”是“这个四边形为菱形”的(必要不充分)条件。
(3)“A= ”是 B= 的(必要不充分)条件。
(4) 的(充分不必要)条件。
(5) 是 的(既不充分也不必要)条件。
(6) , 是 的(充分不必要)条件。
(7) 设, 是 的(充要)条件。
(8)已知a、b、c为非零平面向量。甲:a·b=a·c,是乙:b=c的(必要不充分)条件对“充分条件”、“必要条件” 判定的练习巩固,习题设置具有广度综合性降低 下列四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数。四种命题间的相互关系:原命题
若p则q逆命题
若q则p否命题
若?p则?q逆否命题
若?q则?p互逆互逆互否互否互为 逆否互为 逆否2018/11/27例1 写出下列命题的逆命题、否命题与逆否命题,并判断它们的真假.逆命题: 若ab=0,则a=0.否命题:若a≠0,则ab≠0.逆否命题:若ab≠0,则a≠0. 真真假假(1)若a=0,则ab=0 (2) 若a2>b2,则a>b.逆命题: 若a>b,则a2>b2.否命题:若a2≤b2,则a≤b.逆否命题:若a≤b,则a2≤b2.假假假假(3) 当c>0时,若a>b,则ac>bc.逆命题:当c>0时,若ac>bc,则a>b.否命题:当c>0时,若a≤b,则ac≤bc.逆否命题:当c>0时,若ac≤bc,则a≤b.真真真真(4)四条边相等的四边形是正方形.改写:若一个四边形的四条边相等,则它是正方形.逆命题:若一个四边形是正方形,则它的四条边相等.否命题:若一个四边形的四条边不全相等,则它不是正方形.逆否命题:若一个四边形不是正方形,则它的四条边 不全相等.假真真假 一般地,四种命题的真假性,有而且仅有下面四种情况:通过我们做过的例题,你能从中发现四种命题的真假性间有什么规律吗?真真真真真假假假假假假假假真真真(1)两个命题互为逆否命题,它们有相同的真假性; (2)两个命题为互逆命题或互否命题,它们的真假性没有关系。例3. 写出下列命题的逆命题,否命题,逆否命题,并判断其真假
1.若且,则2.矩形的对角线互相平分且相等
变式:写出下列命题的逆命题,否命题,逆否命题,并判断其真假
1.奇函数的图像关于原点对称
2.若一个三角形有两条边相等,则这个三角形有两个角相等
结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)注意:三种命题中最难写 的是否命题。结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。若一个整数的末位是0,则它可以被5整除。若一条直线到圆心的距离不等于半径,则它不是圆的切线。练习 1、把下列命题改写成“若p则q”的形式: (1)末位是0的整数,可以被5整除;(2)到圆心的距离不等于半径的直线不是圆的切线;2、填空:
(1)命题“末位于0的整数,可以被5整除”的逆命题是:(2)命题“线段的垂直平分线上的点与这条线段两端点的距离相等”的否命题是: (3)命题“对顶角相等”的逆否命题是:(4)命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是:若一个整数可以被5整除,则它的末位是0。若一个点不在线段的垂直平分线上,则它到这条线段两端点的距离不相等。若两个角不相等,则它们不是对顶角。若一条直线是圆的切线,则它到圆心的距离等于半径。
也相等.
(2)如果X2=Y2,则x=-y.
(3)如果a2+b2=0,则a=b=0.
(4)如果a=b=0,则a2+b2=0.
(5)如果A∩B≠φ,则A≠φ.
真假真真真二、新课讲授1、一般地:若p则q为真,记作: 或若p则q为假,记作:(1)如果两个三形全等,那么两三角形面积相等。
(2)“若 则 ”为假命题例如两个三形全等 两三角形面积相等二、新课讲授2、充分条件与必要条件一般地,如果已知 那么我们就说 p是q的充分条件, q是p的必要条件。(1).两个三角形全等 两三角形面积相等。“两个三角形全等”是“两三角形面积相等”的充分条件“两三角形面积相等”是“两个三角形全等 ”的必要条件例如3、充分不必要条件与必要不充分条件一般地,如果已知 且
那么我们就说: p是q的充分不必要条件, q是p的必要不充分条件(1).两个三角形全等 两三角形面积相等但:两三角形面积相等 两个三形全等“两个三角形全等”是“两三角形面积相等”的充分不必要条件“两三角形面积相等”是“两个三角形全等 ”的必要不充分条件4、充要条件一般地,如果已知
即: 那么我们就说: p是q的充要条件, q是p的充要条件例如充分不必要条件必要不充分条件既不充分也不必要条件充分且必要条件(3)“ a2>b2 ”是“ a>b ”的什么条件?(2)“四边形为平行四边形”是“这个四边形为菱形”的什么条件?利用定义解决问题,并寻找判断方法. 目的 pqppqq找p、q判断p q,与
q p的真假根据定义
下结论(1)“a>0,b>0”是“ab>0”的什么条件?(答:充分不必要条件)(答:必要不充分条件)(答:既不充分也不必要条件)例题1: 例题2:说出下列各组命题中,p是q的什么条件?q是p的什么条件? 所以:p是q的充分不必要条件,q是p的必要不充分条件.(2) p: (a-2)(a-3)=0, q: a=3 所以:p是q的必要不充分条件,q是p的充分不必要条件.所以:p与q互为充要条件(4)P: a < b . q: <1 ab所以:p是q的既不充分也不必要的条件
q是p的既不充分也不必要的条件例题3:若A是B 的充要条件,B是C 和D 的必要条件,E是D 的充分条件,E 是A 的充要条件,
则E是B的_______条件,
C是A的________条件,
A是D的________条件,
D是C的_________条件.A BC
DEE BC AA DC D充要条件充分不必要充要条件必要不充分1、已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要条件2.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件练习1.已知p:{x|0
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件 2、已知p:|x+1|>2,q:x2<5x-6,
则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件例5、AA3:填写“充分不必要,必要不充分,充要,既不充分又不必要。
1)sinA>sinB是A>B的_________ 条件。
2)在ΔABC中,sinA>sinB是 A>B的________条件。既不充分又不必要充要条件4、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc2D4、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0
A.充要条件 B必要不充分条件 C充分不必要 D不充分不必要B1.已知 是实数,则“ 且 ”是“ 且 ”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件 2.“ ”是“ ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件 AC【第二组题】
(1) 的(充分不必要)条件。
(2)“四边形为平行四边形”是“这个四边形为菱形”的(必要不充分)条件。
(3)“A= ”是 B= 的(必要不充分)条件。
(4) 的(充分不必要)条件。
(5) 是 的(既不充分也不必要)条件。
(6) , 是 的(充分不必要)条件。
(7) 设, 是 的(充要)条件。
(8)已知a、b、c为非零平面向量。甲:a·b=a·c,是乙:b=c的(必要不充分)条件对“充分条件”、“必要条件” 判定的练习巩固,习题设置具有广度综合性降低 下列四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?若f(x)是正弦函数,则f(x)是周期函数;
若f(x)是周期函数,则f(x)是正弦函数;
若f(x)不是正弦函数,则f(x)不是周期函数;
若f(x)不是周期函数,则f(x)不是正弦函数。四种命题间的相互关系:原命题
若p则q逆命题
若q则p否命题
若?p则?q逆否命题
若?q则?p互逆互逆互否互否互为 逆否互为 逆否2018/11/27例1 写出下列命题的逆命题、否命题与逆否命题,并判断它们的真假.逆命题: 若ab=0,则a=0.否命题:若a≠0,则ab≠0.逆否命题:若ab≠0,则a≠0. 真真假假(1)若a=0,则ab=0 (2) 若a2>b2,则a>b.逆命题: 若a>b,则a2>b2.否命题:若a2≤b2,则a≤b.逆否命题:若a≤b,则a2≤b2.假假假假(3) 当c>0时,若a>b,则ac>bc.逆命题:当c>0时,若ac>bc,则a>b.否命题:当c>0时,若a≤b,则ac≤bc.逆否命题:当c>0时,若ac≤bc,则a≤b.真真真真(4)四条边相等的四边形是正方形.改写:若一个四边形的四条边相等,则它是正方形.逆命题:若一个四边形是正方形,则它的四条边相等.否命题:若一个四边形的四条边不全相等,则它不是正方形.逆否命题:若一个四边形不是正方形,则它的四条边 不全相等.假真真假 一般地,四种命题的真假性,有而且仅有下面四种情况:通过我们做过的例题,你能从中发现四种命题的真假性间有什么规律吗?真真真真真假假假假假假假假真真真(1)两个命题互为逆否命题,它们有相同的真假性; (2)两个命题为互逆命题或互否命题,它们的真假性没有关系。例3. 写出下列命题的逆命题,否命题,逆否命题,并判断其真假
1.若且,则2.矩形的对角线互相平分且相等
变式:写出下列命题的逆命题,否命题,逆否命题,并判断其真假
1.奇函数的图像关于原点对称
2.若一个三角形有两条边相等,则这个三角形有两个角相等
结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)注意:三种命题中最难写 的是否命题。结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。若一个整数的末位是0,则它可以被5整除。若一条直线到圆心的距离不等于半径,则它不是圆的切线。练习 1、把下列命题改写成“若p则q”的形式: (1)末位是0的整数,可以被5整除;(2)到圆心的距离不等于半径的直线不是圆的切线;2、填空:
(1)命题“末位于0的整数,可以被5整除”的逆命题是:(2)命题“线段的垂直平分线上的点与这条线段两端点的距离相等”的否命题是: (3)命题“对顶角相等”的逆否命题是:(4)命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是:若一个整数可以被5整除,则它的末位是0。若一个点不在线段的垂直平分线上,则它到这条线段两端点的距离不相等。若两个角不相等,则它们不是对顶角。若一条直线是圆的切线,则它到圆心的距离等于半径。
