2018-2019学年度第一学期苏科版九年级数学上册2.8圆锥的侧面积同步检测试题含答案
文档属性
| 名称 | 2018-2019学年度第一学期苏科版九年级数学上册2.8圆锥的侧面积同步检测试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 121.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 00:00:00 | ||
图片预览


文档简介
2018-2019学年度第一学期苏科版九年级数学上册_第二章_对称图形-圆
_2.8_圆锥的侧面积_同步检测试题
考试总分: 100 分 考试时间:90分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.一个圆锥的侧面展开图的弧长为,圆心角为,则圆锥的母线长是( )
A. B. C. D.
?2.某杂技团要订做一批无底无盖的圆柱形桶作道具(如图所示),为使小演员表演顺利并且有观赏效果,需圆柱的底面直径为,高为.如果接缝处材料忽略不计,那么一个桶所需材料的面积为( )
A. B.
C. D.
?3.已知圆锥底面的半径是,高是,则这个圆锥侧面展开的扇形的圆心角的度数是( )
A. B. C. D.
?4.用两张全等的矩形纸片分别卷成两个形状不同的柱面(圆柱的侧面),设较高圆柱的侧面积底面半径分别为和,较矮圆柱的侧面积和底面半径分别为和,那么( )
A., B.,
C., D.,
?5.如果圆锥的底面半径为,母线长为,那么它的侧面积等于( )
A. B. C. D.
?6.已知的一条直角边,另一条直角边,以为轴将旋转一周,所得到的圆锥的侧面积是( )
A. B.
C. D.
?7.如图,如果将半径为的圆形纸片剪去一个圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为( )
A. B. C. D.
?8.如果圆柱的轴截面是一个边长为的正方形,那么圆柱的侧面积为( )
A. B. C. D.
?9.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是米,底面半径为米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
A. B. C. D.
?10.底面半径,高为的圆柱与底面半径为,高为的圆柱的体积的比是,则等于( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.某建筑物大厅的圆柱形立柱高米,底面直径为米,则给这根立柱涂上油漆的面积为________平方米.
?12.已知圆锥的母线长为,底面半径为,则圆锥的侧面积等于________.
?13.如图,从半径为的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
?14.已知矩形的一边,另一边,则以直线为轴旋转一周所得到的图形是________,其侧面积是________.
?15.数学活动课上,老师出示如图所示的圆柱形笔筒,让同学们测量并计算笔筒的侧面积,丽丽测得笔筒的底面直径和高分别是和,则笔筒的侧面积是________(精确到)
?16.某校九年班在圣诞节前,为圣诞晚会制作一个如图所示的圆锥形圣诞老人的纸帽,已知圆锥的母线长为,底面直径为,则这个纸帽的表面积为________取
?17.将一个半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是________度.
?18.一个圆锥的底面半径为,母线长为,则圆锥的高是________,侧面展开图的圆心角是________.
?19.将半径为的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________.
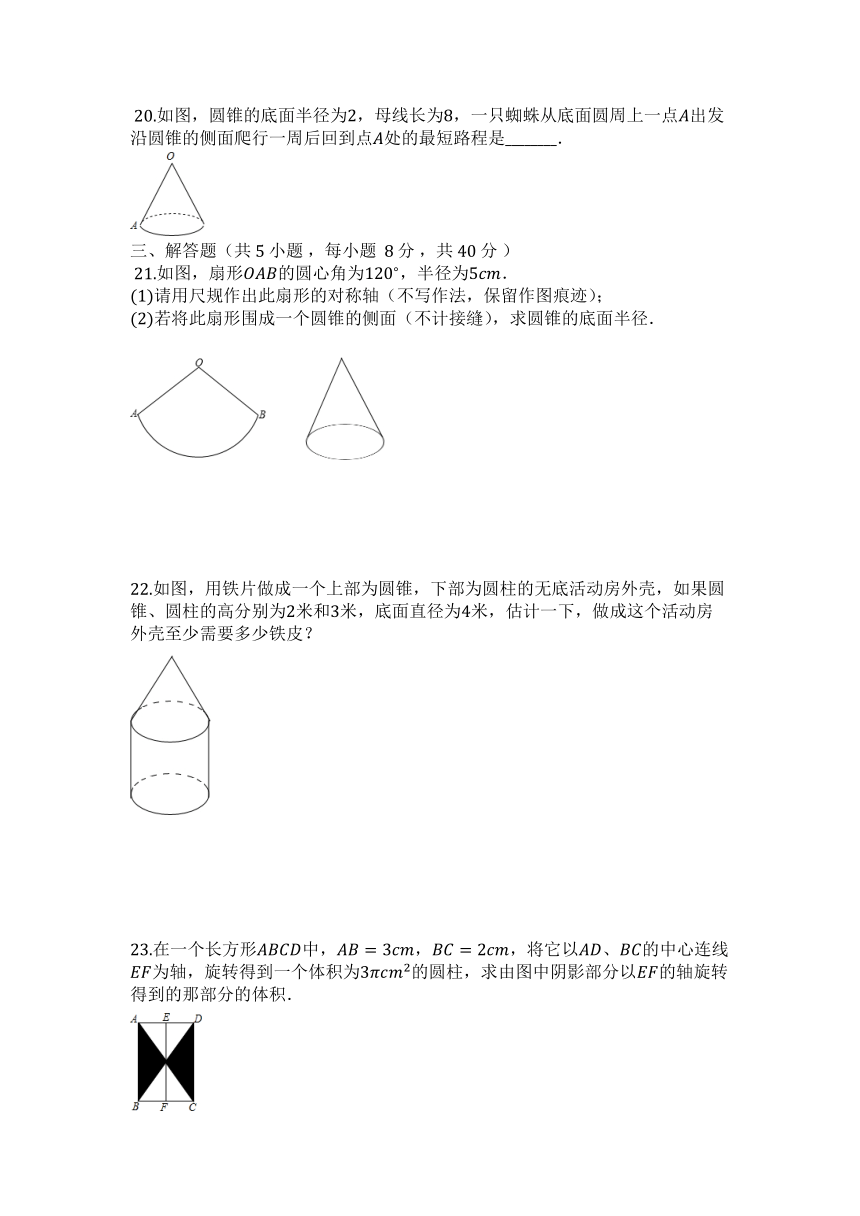
?20.如图,圆锥的底面半径为,母线长为,一只蜘蛛从底面圆周上一点出发沿圆锥的侧面爬行一周后回到点处的最短路程是________.
三、解答题(共 5 小题 ,每小题 8 分 ,共 40 分 )
?21.如图,扇形的圆心角为,半径为.
请用尺规作出此扇形的对称轴(不写作法,保留作图痕迹);
若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面半径.
?
22.如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为米和米,底面直径为米,估计一下,做成这个活动房外壳至少需要多少铁皮?
?
23.在一个长方形中,,,将它以、的中心连线为轴,旋转得到一个体积为的圆柱,求由图中阴影部分以的轴旋转得到的那部分的体积.
?24.如图所示,有一四边形的铁片,,,,.以点为圆心,为半径作圆弧得一扇形.
求阴影部分的面积;
剪下该扇形并用它围成一圆锥的侧面,求该圆锥的底面半径.
?
25.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点、、,请在网格中进行下列操作:
请在图中确定该圆弧所在圆心点的位置,点坐标为________;
连接、,求的半径及扇形的圆心角度数;
若扇形是某一个圆锥的侧面展开图,求该圆锥的底面半径.
答案
1.C
2.C
3.C
4.C
5.B
6.B
7.A
8.A
9.B
10.C
11.
12.
13.
14.圆柱
15.
16.
17.
18.
19.
20.
21.解:直线为扇形的对称轴,如图,
∵扇形的圆心角为,半径为,
∴扇形的弧长,
设圆锥的底面半径为,
∴,
∴.
即圆锥的底面半径为.
22.解:∵圆锥的高为米,底面半径为米,
∴圆锥的母线长为米,
∴圆锥的侧面积为平方米,
圆柱的侧面积为平方米,
∴做成这个活动房外壳至少需要平方米铁皮.
23.解:由题意可得出:阴影部分旋转后体积为两圆锥的组合体,其底面半径为,高为,
故由图中阴影部分以的轴旋转得到的那部分的体积为:.
24.解:在中,∵,,,
∴,,.
∵,,
∵,
∴,
∵,
∴是等边三角形,
∴,.
∴阴影部分的面积扇形的面积的面积;由知弧,
设该圆锥的底面半径为,则
,解得,
故该圆锥的底面半径为.
25.解:如图;
如图;;
作轴,垂足为.
∵,
∴,
又∵,
∴,
∴扇形的圆心角为度;∵弧的长度即为圆锥底面圆的周长.,
设圆锥底面圆半径为,则,
∴.
_2.8_圆锥的侧面积_同步检测试题
考试总分: 100 分 考试时间:90分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.一个圆锥的侧面展开图的弧长为,圆心角为,则圆锥的母线长是( )
A. B. C. D.
?2.某杂技团要订做一批无底无盖的圆柱形桶作道具(如图所示),为使小演员表演顺利并且有观赏效果,需圆柱的底面直径为,高为.如果接缝处材料忽略不计,那么一个桶所需材料的面积为( )
A. B.
C. D.
?3.已知圆锥底面的半径是,高是,则这个圆锥侧面展开的扇形的圆心角的度数是( )
A. B. C. D.
?4.用两张全等的矩形纸片分别卷成两个形状不同的柱面(圆柱的侧面),设较高圆柱的侧面积底面半径分别为和,较矮圆柱的侧面积和底面半径分别为和,那么( )
A., B.,
C., D.,
?5.如果圆锥的底面半径为,母线长为,那么它的侧面积等于( )
A. B. C. D.
?6.已知的一条直角边,另一条直角边,以为轴将旋转一周,所得到的圆锥的侧面积是( )
A. B.
C. D.
?7.如图,如果将半径为的圆形纸片剪去一个圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为( )
A. B. C. D.
?8.如果圆柱的轴截面是一个边长为的正方形,那么圆柱的侧面积为( )
A. B. C. D.
?9.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是米,底面半径为米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
A. B. C. D.
?10.底面半径,高为的圆柱与底面半径为,高为的圆柱的体积的比是,则等于( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.某建筑物大厅的圆柱形立柱高米,底面直径为米,则给这根立柱涂上油漆的面积为________平方米.
?12.已知圆锥的母线长为,底面半径为,则圆锥的侧面积等于________.
?13.如图,从半径为的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
?14.已知矩形的一边,另一边,则以直线为轴旋转一周所得到的图形是________,其侧面积是________.
?15.数学活动课上,老师出示如图所示的圆柱形笔筒,让同学们测量并计算笔筒的侧面积,丽丽测得笔筒的底面直径和高分别是和,则笔筒的侧面积是________(精确到)
?16.某校九年班在圣诞节前,为圣诞晚会制作一个如图所示的圆锥形圣诞老人的纸帽,已知圆锥的母线长为,底面直径为,则这个纸帽的表面积为________取
?17.将一个半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是________度.
?18.一个圆锥的底面半径为,母线长为,则圆锥的高是________,侧面展开图的圆心角是________.
?19.将半径为的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________.
?20.如图,圆锥的底面半径为,母线长为,一只蜘蛛从底面圆周上一点出发沿圆锥的侧面爬行一周后回到点处的最短路程是________.
三、解答题(共 5 小题 ,每小题 8 分 ,共 40 分 )
?21.如图,扇形的圆心角为,半径为.
请用尺规作出此扇形的对称轴(不写作法,保留作图痕迹);
若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面半径.
?
22.如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为米和米,底面直径为米,估计一下,做成这个活动房外壳至少需要多少铁皮?
?
23.在一个长方形中,,,将它以、的中心连线为轴,旋转得到一个体积为的圆柱,求由图中阴影部分以的轴旋转得到的那部分的体积.
?24.如图所示,有一四边形的铁片,,,,.以点为圆心,为半径作圆弧得一扇形.
求阴影部分的面积;
剪下该扇形并用它围成一圆锥的侧面,求该圆锥的底面半径.
?
25.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点、、,请在网格中进行下列操作:
请在图中确定该圆弧所在圆心点的位置,点坐标为________;
连接、,求的半径及扇形的圆心角度数;
若扇形是某一个圆锥的侧面展开图,求该圆锥的底面半径.
答案
1.C
2.C
3.C
4.C
5.B
6.B
7.A
8.A
9.B
10.C
11.
12.
13.
14.圆柱
15.
16.
17.
18.
19.
20.
21.解:直线为扇形的对称轴,如图,
∵扇形的圆心角为,半径为,
∴扇形的弧长,
设圆锥的底面半径为,
∴,
∴.
即圆锥的底面半径为.
22.解:∵圆锥的高为米,底面半径为米,
∴圆锥的母线长为米,
∴圆锥的侧面积为平方米,
圆柱的侧面积为平方米,
∴做成这个活动房外壳至少需要平方米铁皮.
23.解:由题意可得出:阴影部分旋转后体积为两圆锥的组合体,其底面半径为,高为,
故由图中阴影部分以的轴旋转得到的那部分的体积为:.
24.解:在中,∵,,,
∴,,.
∵,,
∵,
∴,
∵,
∴是等边三角形,
∴,.
∴阴影部分的面积扇形的面积的面积;由知弧,
设该圆锥的底面半径为,则
,解得,
故该圆锥的底面半径为.
25.解:如图;
如图;;
作轴,垂足为.
∵,
∴,
又∵,
∴,
∴扇形的圆心角为度;∵弧的长度即为圆锥底面圆的周长.,
设圆锥底面圆半径为,则,
∴.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
