2018年高中数学第2章圆锥曲线与方程2.2.1椭圆的标准方程课件4苏教版选修2_1(20张)
文档属性
| 名称 | 2018年高中数学第2章圆锥曲线与方程2.2.1椭圆的标准方程课件4苏教版选修2_1(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 829.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-29 15:07:49 | ||
图片预览







文档简介
课件20张PPT。第一课时2.2.1椭圆的标准方程感受生活中的椭圆一.问题情境问题1:如何精确地设计、制作出现实生活中这些椭圆形的物件呢?
问题2:如何建立椭圆的方程? 学习目标:
1.理解椭圆标准方程的推导。
2.掌握椭圆的标准方程,会根据条件求椭圆的标准方程,
复习回顾 1、椭圆的定义?焦点?焦距? 平面内到两个定点F1,F2的距离的和等于常数 ( 大于F1F2 )的点的轨迹——椭圆.两个定点F1,F2——椭圆的焦点.
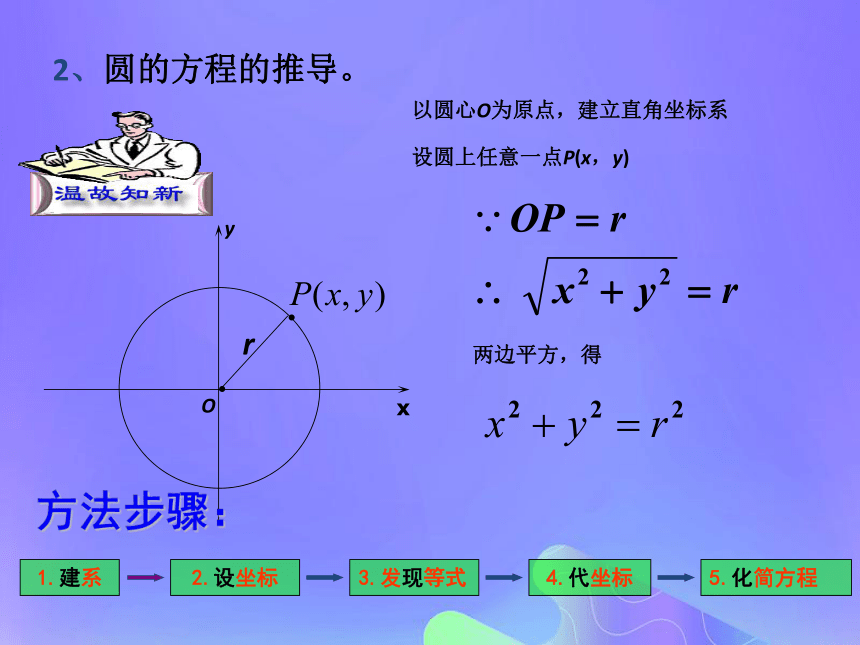
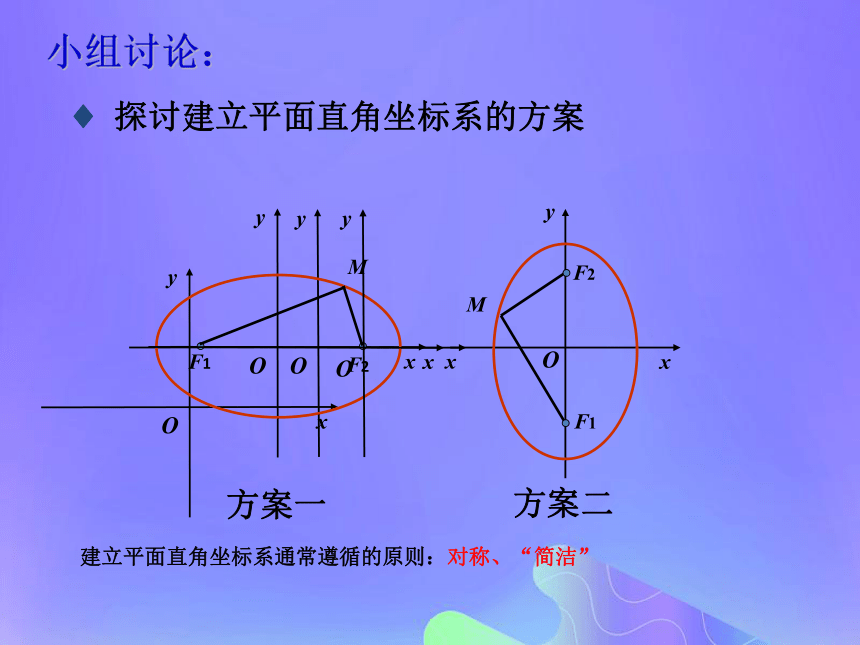
两焦点间的距离——椭圆的焦距.通常:焦距记为2c,椭圆上任意一点P到F1,F2 的距离的和记为2a,(2a>2c)Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.发现等式4.代坐标方法步骤: 5.化简方程2、圆的方程的推导。小组讨论:? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一椭圆方程的建立
(选择方案1,小组交流并尝试)步骤一:建立直角坐标系步骤二:设动点坐标步骤四:代入坐标步骤五:化简方程步骤三:发现等式解:以F1、F2所在的直线为x轴,线段F1F2的垂直平分线为y轴,
建立平面直角坐标系(如图).则F1、F2的坐标分别是(?c,0)、(c,0) .
设M(x, y)为椭圆上任意一点,3.建构数学(问题:下面怎样化简?)(现)由椭圆的定义得:代入坐标1)椭圆的标准方程的推导步骤五:化简方程两边再平方得:
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,整理得:(a2-c2)x2+a2y2=a2(a2-c2).移项得: ,两边平方得:
,整理得: .步骤五:化简方程因为a2(a2-c2) ≠0,所以两边同除以a2(a2-c2)得:
,又因为a2-c2>0,所以可设a2-c2=
b2(b>0),于是得:
.总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:2)椭圆的标准方程观察思考:如何根据标准方程判断焦点在哪个坐标轴上? 椭圆的焦点位置可由方程中x2与
y2的分母的大小来确定,焦点在分母
大的项所对应的坐标轴上. 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系a2=b2+c2
MF1+MF2=2a (2a>2c>0)定 义3)两类标准方程的对照表1.口答:下列方程是否表示椭圆? 若是,则判定其焦点在何轴?并指明 ,写出焦点坐标.小试牛刀:2、 已知椭圆的方程为: , 请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___. 5436(-3,0)、(3,0)8
例1、写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
或数学应用(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经过点P( -1.5 ,2.5).求椭圆标准方程的步骤:解题反思①定位:确定焦点所在的坐标轴;②定量:求a, b的值.练习:1、求适合下列条件的椭圆的标准方程: (1) a =4,b=3,焦点在 y 轴上;
(2) b =1,c= ,焦点在坐标轴上;
(3) 两个焦点的坐标是( -3,0)和( 3,0),
并且经过点P( 0,2).
(4)焦点在x轴上,焦距是4,且经过点(3, )小结与反思1.方程建立的过程:2.椭圆的标准方程:3.求椭圆的标准方程:建、设、现、代、化①定位:确定焦点所在的坐标轴;②定量:求a, b的值.
2.掌握椭圆的标准方程,会根据条件求椭圆的标准方程,
复习回顾 1、椭圆的定义?焦点?焦距? 平面内到两个定点F1,F2的距离的和等于常数 ( 大于F1F2 )的点的轨迹——椭圆.两个定点F1,F2——椭圆的焦点.
两焦点间的距离——椭圆的焦距.通常:焦距记为2c,椭圆上任意一点P到F1,F2 的距离的和记为2a,(2a>2c)Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.发现等式4.代坐标方法步骤: 5.化简方程2、圆的方程的推导。小组讨论:? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一椭圆方程的建立
(选择方案1,小组交流并尝试)步骤一:建立直角坐标系步骤二:设动点坐标步骤四:代入坐标步骤五:化简方程步骤三:发现等式解:以F1、F2所在的直线为x轴,线段F1F2的垂直平分线为y轴,
建立平面直角坐标系(如图).则F1、F2的坐标分别是(?c,0)、(c,0) .
设M(x, y)为椭圆上任意一点,3.建构数学(问题:下面怎样化简?)(现)由椭圆的定义得:代入坐标1)椭圆的标准方程的推导步骤五:化简方程两边再平方得:
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,整理得:(a2-c2)x2+a2y2=a2(a2-c2).移项得: ,两边平方得:
,整理得: .步骤五:化简方程因为a2(a2-c2) ≠0,所以两边同除以a2(a2-c2)得:
,又因为a2-c2>0,所以可设a2-c2=
b2(b>0),于是得:
.总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:2)椭圆的标准方程观察思考:如何根据标准方程判断焦点在哪个坐标轴上? 椭圆的焦点位置可由方程中x2与
y2的分母的大小来确定,焦点在分母
大的项所对应的坐标轴上. 图 形方 程焦 点F(±c,0)F(0,±c)a,b,c之间的关系a2=b2+c2
MF1+MF2=2a (2a>2c>0)定 义3)两类标准方程的对照表1.口答:下列方程是否表示椭圆? 若是,则判定其焦点在何轴?并指明 ,写出焦点坐标.小试牛刀:2、 已知椭圆的方程为: , 请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且CF1=2,则CF2=___. 5436(-3,0)、(3,0)8
例1、写出适合下列条件的椭圆的标准方程 (1) a =4,b=1,焦点在 x 轴上;
(2) a =4,b=1,焦点在坐标轴上;
或数学应用(3) 两个焦点的坐标是( 0 ,-2)和( 0 ,2),并且经过点P( -1.5 ,2.5).求椭圆标准方程的步骤:解题反思①定位:确定焦点所在的坐标轴;②定量:求a, b的值.练习:1、求适合下列条件的椭圆的标准方程: (1) a =4,b=3,焦点在 y 轴上;
(2) b =1,c= ,焦点在坐标轴上;
(3) 两个焦点的坐标是( -3,0)和( 3,0),
并且经过点P( 0,2).
(4)焦点在x轴上,焦距是4,且经过点(3, )小结与反思1.方程建立的过程:2.椭圆的标准方程:3.求椭圆的标准方程:建、设、现、代、化①定位:确定焦点所在的坐标轴;②定量:求a, b的值.
