2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 559.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-29 00:00:00 | ||
图片预览





文档简介
课件20张PPT。抛物线及其标准方程
OyxFMl复习提问:(1)当0<e <1时,点M的轨迹是什么?(2)当e>1时,点M的轨迹是什么?
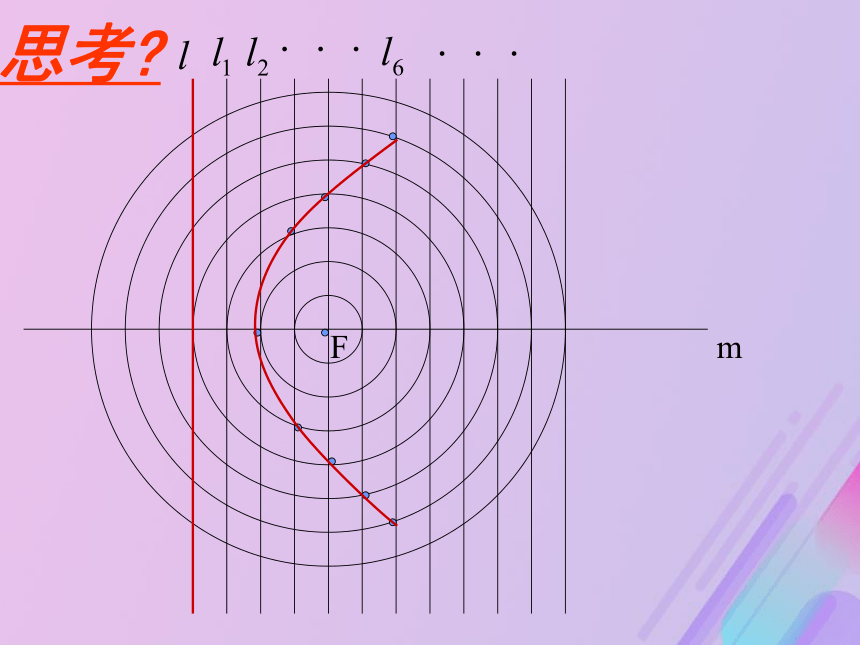
是椭圆是双曲线mF思考?
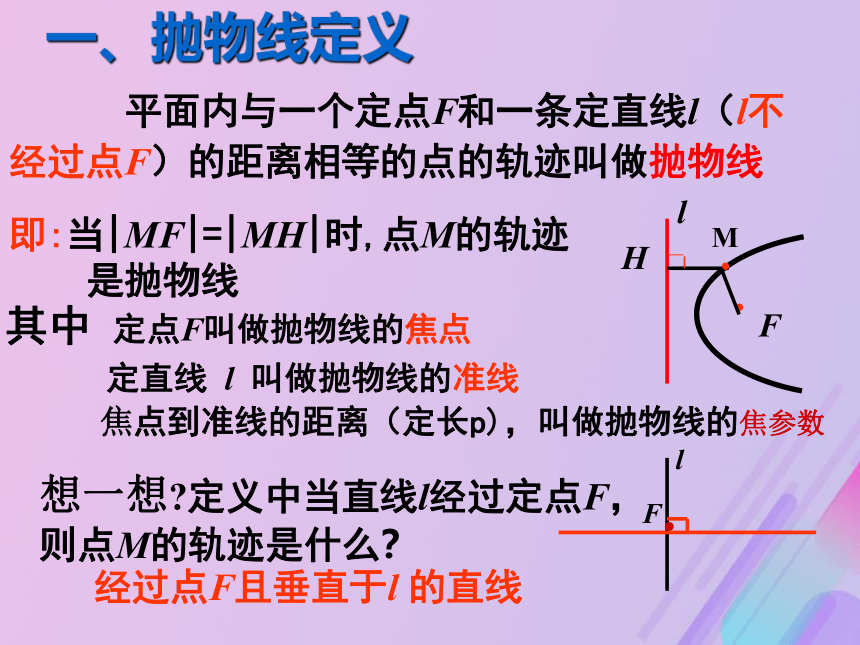
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
一、抛物线定义想一想?定义中当直线l经过定点F,则点M的轨迹是什么? 其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线即:当|MF|=|MH|时,点M的轨迹
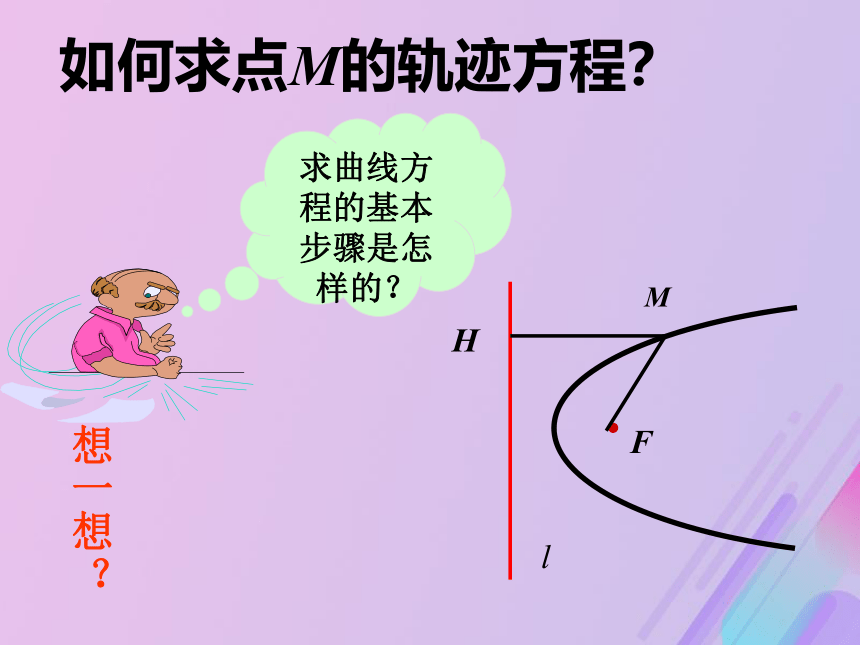
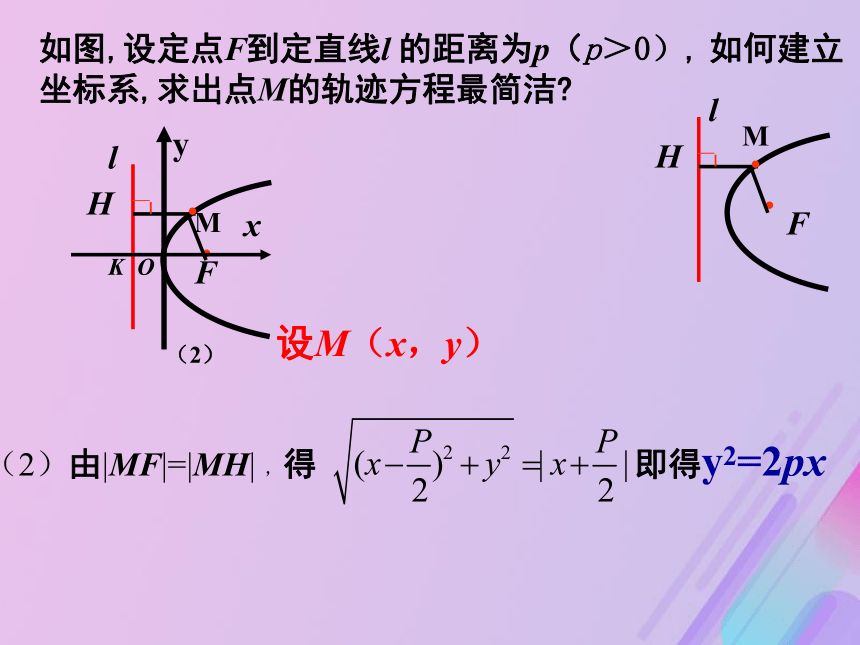
是抛物线 经过点F且垂直于l 的直线焦点到准线的距离(定长p),叫做抛物线的焦参数感受生活中抛物线图形的例子阳春三桥春湾镇那乌古桥如何求点M的轨迹方程?求曲线方程的基本步骤是怎样的?想一想?回顾求曲线方程一般步骤:1、建系、设点2、写出适合条件P的点M的集合3、列方程4、化简5、证明(可省略)如图,设定点F到定直线l 的距离为p(p>0), 如何建立坐标系,求出点M的轨迹方程最简洁?(2)由|MF|=|MH| ,得 即得y2=2px设M(x,y) 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦点到准线的距离一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.二、标准方程四种抛物线的标准方程对比感悟归结:1、焦点在一次项字母对应的坐标轴上. 2、一次项的系数的符号决定了抛物线的开口方向.
3、焦点坐标的非零坐标是一次项系数的 .
4、准线方程对应的数是一次项系数的 的
相反数.
例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;解: ∵2P=6,∴P=3
所以抛物线的焦点坐标是( ,0)
准线方程是x=
变式:写出下列抛物线的标准方程、焦点坐标和准
线方程:
(1) 6y+5x2=0 ;(2)y=6ax2(a≠0).
(2)x2 = y , 焦点坐标为( 0 , ),
准线方程是y=
解:(1) x2 = y ,焦点坐标为( 0, ),
准线方程是y=
变式:写出下列抛物线的标准方程、焦点坐 标和准线方程:
(1) 6y+5x2=0 ; (2)y=6ax2(a≠0) .
感悟 :求抛线的焦点坐标和准线方程要先化成抛物线的标准方程例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,所以设所
求的标准方程为x2= -2py
由题意得 ,即p=4
∴所求的标准方程为x2= -8y分析:因为焦点坐标是(0,-2),所以抛物线开口方向是y轴的负方向,它的方程形式为x2= -2py.待定系数法求抛物线标准方程例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,所以设所
求的标准方程为x2= -2py
即 得p=4
∴所求的标准方程为x2= -8y分析:因为焦点坐标是(0,-2),所以抛物线开口方向是y轴的负方向,它的方程形式为x2= -2py.(1)焦点是F(-2,0),它的标准方程_______.
(2)准线方程是y = -2,它的标准方程_______.
(3)焦点到准线的距离是4,它的标准方程_____.
变式:y2=-8xx2=8yx2=±8y 、y2=±8x
(1)(2)解题感悟:用待定系数法求抛物线标准方程的步骤:(1)确定抛物线的形式.(2)求p值(3)写抛物线方程注意:焦点或开口方向不定,则要注意分类讨论 求过点A(-3,2)的抛物线的标准方程。
解:(1)当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= (2)当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
巩固提高:1、理解抛物线的定义,标准方程类型.2、会求不同类型抛物线的焦点坐标、准线方程3、掌握用待定系数法求抛物线标准方程
4、注重数形结合和分类讨论的解题方法.小结变式训练1.根据下列条件写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程是x=1/4;
(3)焦点到准线的距离是2;
(4)焦点在直线3x-4y-12=0上.
2.求下列抛物线的焦点坐标与准线方程
(1)y2=28x;
(2)4x2=3y;
(3)2y2+5x=0;
(4)y=4ax2y2=12xy2=-xy2=4x或y2=-4x或x2=4y或x2=-4yy2=16x或x2=-12y焦点(7,0),准线x=-7焦点(0,1/16a),
准线y=-1/16a;
焦点(0,3/16),准线y=-3/16焦点(-5/8,0),准线x=5/8
OyxFMl复习提问:(1)当0<e <1时,点M的轨迹是什么?(2)当e>1时,点M的轨迹是什么?
是椭圆是双曲线mF思考?
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
一、抛物线定义想一想?定义中当直线l经过定点F,则点M的轨迹是什么? 其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线即:当|MF|=|MH|时,点M的轨迹
是抛物线 经过点F且垂直于l 的直线焦点到准线的距离(定长p),叫做抛物线的焦参数感受生活中抛物线图形的例子阳春三桥春湾镇那乌古桥如何求点M的轨迹方程?求曲线方程的基本步骤是怎样的?想一想?回顾求曲线方程一般步骤:1、建系、设点2、写出适合条件P的点M的集合3、列方程4、化简5、证明(可省略)如图,设定点F到定直线l 的距离为p(p>0), 如何建立坐标系,求出点M的轨迹方程最简洁?(2)由|MF|=|MH| ,得 即得y2=2px设M(x,y) 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦点到准线的距离一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.二、标准方程四种抛物线的标准方程对比感悟归结:1、焦点在一次项字母对应的坐标轴上. 2、一次项的系数的符号决定了抛物线的开口方向.
3、焦点坐标的非零坐标是一次项系数的 .
4、准线方程对应的数是一次项系数的 的
相反数.
例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;解: ∵2P=6,∴P=3
所以抛物线的焦点坐标是( ,0)
准线方程是x=
变式:写出下列抛物线的标准方程、焦点坐标和准
线方程:
(1) 6y+5x2=0 ;(2)y=6ax2(a≠0).
(2)x2 = y , 焦点坐标为( 0 , ),
准线方程是y=
解:(1) x2 = y ,焦点坐标为( 0, ),
准线方程是y=
变式:写出下列抛物线的标准方程、焦点坐 标和准线方程:
(1) 6y+5x2=0 ; (2)y=6ax2(a≠0) .
感悟 :求抛线的焦点坐标和准线方程要先化成抛物线的标准方程例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,所以设所
求的标准方程为x2= -2py
由题意得 ,即p=4
∴所求的标准方程为x2= -8y分析:因为焦点坐标是(0,-2),所以抛物线开口方向是y轴的负方向,它的方程形式为x2= -2py.待定系数法求抛物线标准方程例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,所以设所
求的标准方程为x2= -2py
即 得p=4
∴所求的标准方程为x2= -8y分析:因为焦点坐标是(0,-2),所以抛物线开口方向是y轴的负方向,它的方程形式为x2= -2py.(1)焦点是F(-2,0),它的标准方程_______.
(2)准线方程是y = -2,它的标准方程_______.
(3)焦点到准线的距离是4,它的标准方程_____.
变式:y2=-8xx2=8yx2=±8y 、y2=±8x
(1)(2)解题感悟:用待定系数法求抛物线标准方程的步骤:(1)确定抛物线的形式.(2)求p值(3)写抛物线方程注意:焦点或开口方向不定,则要注意分类讨论 求过点A(-3,2)的抛物线的标准方程。
解:(1)当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= (2)当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
巩固提高:1、理解抛物线的定义,标准方程类型.2、会求不同类型抛物线的焦点坐标、准线方程3、掌握用待定系数法求抛物线标准方程
4、注重数形结合和分类讨论的解题方法.小结变式训练1.根据下列条件写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程是x=1/4;
(3)焦点到准线的距离是2;
(4)焦点在直线3x-4y-12=0上.
2.求下列抛物线的焦点坐标与准线方程
(1)y2=28x;
(2)4x2=3y;
(3)2y2+5x=0;
(4)y=4ax2y2=12xy2=-xy2=4x或y2=-4x或x2=4y或x2=-4yy2=16x或x2=-12y焦点(7,0),准线x=-7焦点(0,1/16a),
准线y=-1/16a;
焦点(0,3/16),准线y=-3/16焦点(-5/8,0),准线x=5/8
