2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件8新人教B版选修2_1(20张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件8新人教B版选修2_1(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 288.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-29 00:00:00 | ||
图片预览







文档简介
课件20张PPT。椭圆的简单几何性质 掌握椭圆的简单几何性质。
并能利用椭圆的性质解决实际问题。
培养学生观察分析,类比猜想,逻辑推理的
思维能力及用数形结合思想解决问题的能力。 通过自主探究、合作交流激发学生学习兴趣和探索问题的勇气,培养良好的思维品质。教学目标重点:从知识上来讲,要掌握椭圆的范围、对称性、顶点的概念、离心率及其应用;从学生的体验来说,需要关注学生在探究椭圆性质的过程中思维层次的展现和思维能力的提高。难点:由曲线方程来研究其几何性质,由几何性质研究曲线方程,由数形结合思想方法研究离心率。重点、难点教学过程1.创设情境,提出问题 2010年10月1日下午十八时,随着一声巨响,我国研制的嫦娥二号载人飞船,从西昌卫星发射中心顺利升空,不久,飞船进入了以近地点200公里,远地点347公里的椭圆轨道围绕地球运行,举世瞩目,万众欢腾。请问你能利用所学的知识求出椭圆轨道的方程吗?你想知道椭圆有哪些重要的几何性质吗?今天这一节课我们就来探讨这些问题。椭圆性质1:范围提出问题:1、上节课我们学习了椭圆的标准方程,其实椭圆特别像一种什么水果?2、如果新疆的哈密瓜要出口了,我们要对它进行包装,你会选择什么样的盒子包装?3、我们能否把椭圆也包装一下呢?这就是我们要研究的椭圆的第一个性质----范围1、范围: -a≤x≤a, -b≤y≤b 知
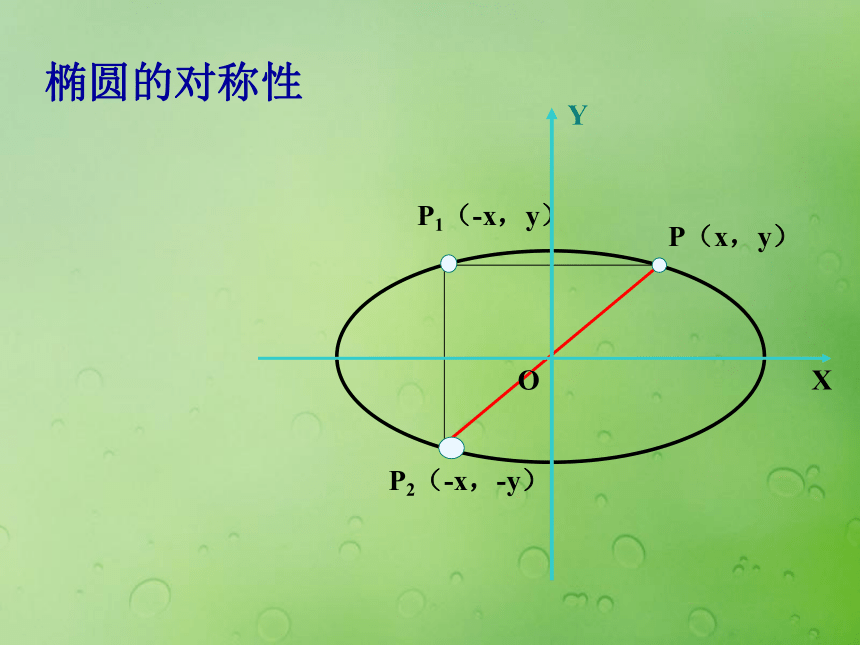
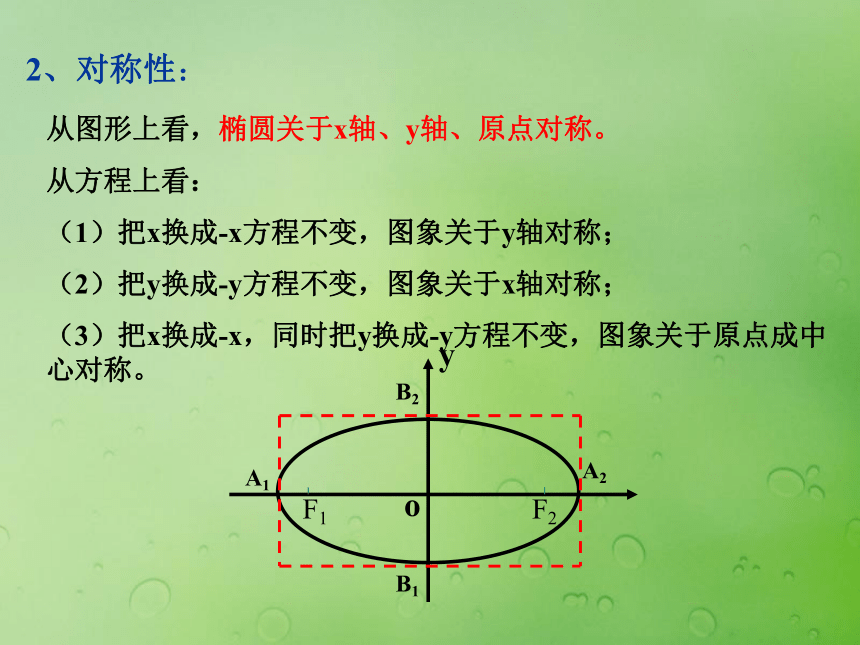
椭圆落在x=±a,y= ± b组成的矩形中椭圆的对称性2、对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。 oyB2B1A1A2F1F23、椭圆的顶点令 x=0,得 y=? 说明椭圆与 y轴的交点?
令 y=0,得 x=? 说明椭圆与 x轴的交点?顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。 oyB2B1A1A2F1F2B1 A2 B2 B2 B1 A1 A1 A2 引导:两个椭圆方程的异同点是什么?探究一:在a不变的情况下,随b的变化椭圆的形状如何变化的?
探究二:①若 的值变大时,椭圆的形状如何变化?②若 的值变小时,椭圆的形状又如何变化?4、椭圆的离心率e (刻画椭圆扁平程度的量)离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:02)e 越接近 0,c 就越接近 0,则 b就越大,椭圆就越圆思考:当e=0时,曲线是什么? |x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前例1.已知椭圆方程9x2+25y2=225, 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 顶点坐标是:
外切矩形的面积等于: 。 106860(±4,0) (±5,0),(0,±3)练习
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1练习:已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0) 、Q(0,-2) ;
(2)长轴长等于20,离心率等于. 本节课通过师生的共同努力,借助椭圆的方程研究了椭圆的范围、对称性、顶点、离心率及其简单应用,回顾研讨过程,突出了方程的作用,加深了对解析法(用代数的方法研究几何问题)的认识,体现了数形结合思想的应用.课堂小结当堂检测(时量:5分钟 满分:10分)
1.椭圆以坐标轴为对称轴,离心率 e= ,长轴长为6,则椭圆的方程 为( )
A. B.
C. 或 D. 或
2. 若椭圆的一个焦点与短轴的两端点构成一个正三角形,则椭圆的离心率e =_____.四、板书设计2.2椭圆简单的几何性质1、范围:2、对称性:3、椭圆的顶点:4、椭圆的离心率e例1例2
并能利用椭圆的性质解决实际问题。
培养学生观察分析,类比猜想,逻辑推理的
思维能力及用数形结合思想解决问题的能力。 通过自主探究、合作交流激发学生学习兴趣和探索问题的勇气,培养良好的思维品质。教学目标重点:从知识上来讲,要掌握椭圆的范围、对称性、顶点的概念、离心率及其应用;从学生的体验来说,需要关注学生在探究椭圆性质的过程中思维层次的展现和思维能力的提高。难点:由曲线方程来研究其几何性质,由几何性质研究曲线方程,由数形结合思想方法研究离心率。重点、难点教学过程1.创设情境,提出问题 2010年10月1日下午十八时,随着一声巨响,我国研制的嫦娥二号载人飞船,从西昌卫星发射中心顺利升空,不久,飞船进入了以近地点200公里,远地点347公里的椭圆轨道围绕地球运行,举世瞩目,万众欢腾。请问你能利用所学的知识求出椭圆轨道的方程吗?你想知道椭圆有哪些重要的几何性质吗?今天这一节课我们就来探讨这些问题。椭圆性质1:范围提出问题:1、上节课我们学习了椭圆的标准方程,其实椭圆特别像一种什么水果?2、如果新疆的哈密瓜要出口了,我们要对它进行包装,你会选择什么样的盒子包装?3、我们能否把椭圆也包装一下呢?这就是我们要研究的椭圆的第一个性质----范围1、范围: -a≤x≤a, -b≤y≤b 知
椭圆落在x=±a,y= ± b组成的矩形中椭圆的对称性2、对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。 oyB2B1A1A2F1F23、椭圆的顶点令 x=0,得 y=? 说明椭圆与 y轴的交点?
令 y=0,得 x=? 说明椭圆与 x轴的交点?顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。 oyB2B1A1A2F1F2B1 A2 B2 B2 B1 A1 A1 A2 引导:两个椭圆方程的异同点是什么?探究一:在a不变的情况下,随b的变化椭圆的形状如何变化的?
探究二:①若 的值变大时,椭圆的形状如何变化?②若 的值变小时,椭圆的形状又如何变化?4、椭圆的离心率e (刻画椭圆扁平程度的量)离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:0
焦距是: 。 离心率等于: 。
焦点坐标是: 顶点坐标是:
外切矩形的面积等于: 。 106860(±4,0) (±5,0),(0,±3)练习
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1练习:已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0) 、Q(0,-2) ;
(2)长轴长等于20,离心率等于. 本节课通过师生的共同努力,借助椭圆的方程研究了椭圆的范围、对称性、顶点、离心率及其简单应用,回顾研讨过程,突出了方程的作用,加深了对解析法(用代数的方法研究几何问题)的认识,体现了数形结合思想的应用.课堂小结当堂检测(时量:5分钟 满分:10分)
1.椭圆以坐标轴为对称轴,离心率 e= ,长轴长为6,则椭圆的方程 为( )
A. B.
C. 或 D. 或
2. 若椭圆的一个焦点与短轴的两端点构成一个正三角形,则椭圆的离心率e =_____.四、板书设计2.2椭圆简单的几何性质1、范围:2、对称性:3、椭圆的顶点:4、椭圆的离心率e例1例2
