2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件9新人教B版选修2_1(19张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件9新人教B版选修2_1(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 493.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-29 15:31:50 | ||
图片预览






文档简介
课件19张PPT。双曲线的几何性质 YXF1F2A1A2B1B2双曲线图形(1)双曲线的图形与几何性质(1)双曲线标准方程:YX双曲线性质:1、范围:x≥a或x≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=双曲线的图形与几何性质(1)双曲线标准方程:YX双曲线性质:1、范围:x≥a 或
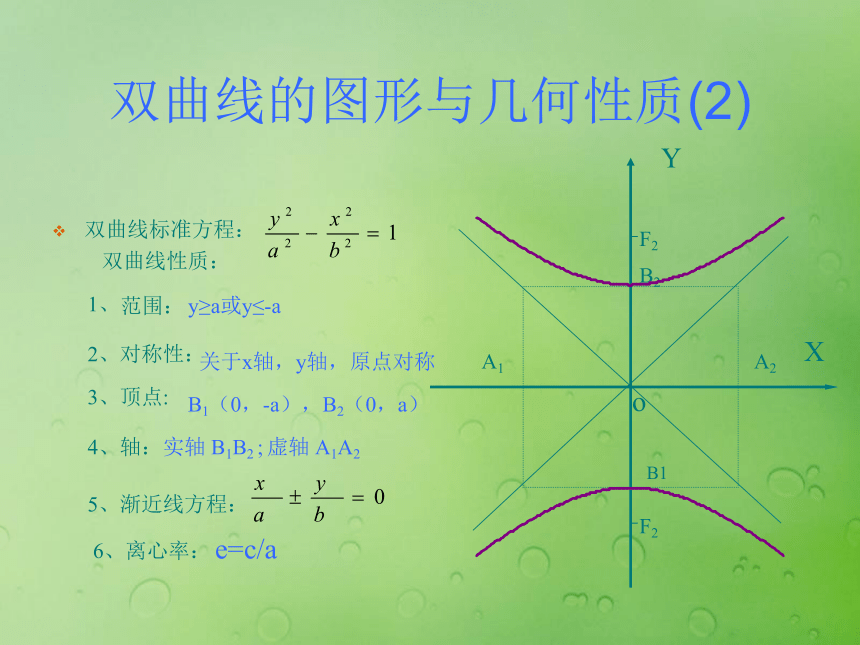
2、对称性:关于x轴,y轴,原点对称。3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=XYF1F2OB1B2A2A1双曲线图形(2)双曲线的图形与几何性质(2)双曲线标准方程:YX双曲线性质:1、范围:y≥a或y≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:B1(0,-a),B2(0,a)4、轴:实轴 B1B2 ; 虚轴 A1A2A1A2B1B25、渐近线方程:6、离心率:e=c/aF2F2o例题1:求双曲线的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(-5,0),(5,0)离心率:渐近线方程:练习题1:填表|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)例2:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原
双曲线的共轭双曲线,求证:
(1)双曲线和它的共轭双曲线有共同的渐近线;
(2)双曲线和它的共轭双曲线的四个焦点在同一个圆上.证明:(1)设已知双曲线的方程是:则它的共轭双曲线方程是:渐近线为渐近线为:显然,它可化为故双曲线和它的共轭双曲线有共同的渐近线;证明:(2)设已知双曲线的焦点为F(c,0),F(-c,0)它的共轭双曲线的焦点为F1’(0,c’), F2’(0,-c’),∵∴ c=c'∴四个焦点 , 在同一个圆YXA1A2B1B2F1F2oF’2F’1问:有相同渐近线的双曲线方
程一定是共轭双曲线吗一、选择题:一、选择题:一、选择题:一、选择题:一、选择题:二、填空题二、填空题二、填空题:二、填空题:小结(注意研究方法):1.范围
2.对称性
3.顶点,实轴 、虚轴
4.渐近线
5.离心率
2、对称性:关于x轴,y轴,原点对称3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=双曲线的图形与几何性质(1)双曲线标准方程:YX双曲线性质:1、范围:x≥a 或
2、对称性:关于x轴,y轴,原点对称。3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=XYF1F2OB1B2A2A1双曲线图形(2)双曲线的图形与几何性质(2)双曲线标准方程:YX双曲线性质:1、范围:y≥a或y≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:B1(0,-a),B2(0,a)4、轴:实轴 B1B2 ; 虚轴 A1A2A1A2B1B25、渐近线方程:6、离心率:e=c/aF2F2o例题1:求双曲线的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(-5,0),(5,0)离心率:渐近线方程:练习题1:填表|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)例2:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原
双曲线的共轭双曲线,求证:
(1)双曲线和它的共轭双曲线有共同的渐近线;
(2)双曲线和它的共轭双曲线的四个焦点在同一个圆上.证明:(1)设已知双曲线的方程是:则它的共轭双曲线方程是:渐近线为渐近线为:显然,它可化为故双曲线和它的共轭双曲线有共同的渐近线;证明:(2)设已知双曲线的焦点为F(c,0),F(-c,0)它的共轭双曲线的焦点为F1’(0,c’), F2’(0,-c’),∵∴ c=c'∴四个焦点 , 在同一个圆YXA1A2B1B2F1F2oF’2F’1问:有相同渐近线的双曲线方
程一定是共轭双曲线吗一、选择题:一、选择题:一、选择题:一、选择题:一、选择题:二、填空题二、填空题二、填空题:二、填空题:小结(注意研究方法):1.范围
2.对称性
3.顶点,实轴 、虚轴
4.渐近线
5.离心率
