第4章 锐角三角函数单元测试B卷(含解析)
文档属性
| 名称 | 第4章 锐角三角函数单元测试B卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-29 19:50:04 | ||
图片预览



文档简介
九年级上册第四章锐角三角函数单元测试B卷
考试时间:120分钟 满分:120分 姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1. 在△ABC中,∠C=90°,如果AB=6,BC=3,那么cosB的值是(?? )
A.??????????????????????????????????????? B.?????????????????????????????????????? C.?????????????????????????????????????? D.?
2. 已知sin35°=cosα,则α为(???? )
A.?35°????????????????????????????????????? ??B.?55°???????????????????????????????????????C.?75°???????????????????????????? ???????????D.?65°
3. 在 中, , 若cosB= ,则sinA的值为 (?? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
4. 若锐角α满足sinα> ,且cosα> ,则α的范围是(?? )
A.?0°<α<30°????????????????????B.?30°<α<60°????????????????????C.?60°<α<90°????????????????????D.?45°<α<90°
5. 在Rt△ABC中, , , ,下列选项中一定正确的是( ??)
A.?;????????????????? B.?;???????????????? C.?;????????????????? D.?.
6. 在△ABC中,∠A,∠B都是锐角,tanA=1,sinB= ,你认为△ABC最确切的判断是(??? )
A.?等腰三角形?????????????????? B.?等腰直角三角形?????????????????? C.?直角三角形??????????????????? D.?锐角三角形
7. △ABC中,∠A,∠B均为锐角,且(tanB﹣ )(2sinA﹣ )=0,则△ABC一定是(?? )
A.等腰三角形 B.等边三角形 C.直角三角形 D.有一个角是60°的三角形
8. 如图,△ABC中,∠C=90°,AC=16cm,AB的中垂线MN交AC于点D,连接BD,若cos∠BDC= ?,则BC=(?? ) A.?8cm??????????????????? ?B.?4cm???????????????????? ?C.?6cm?????????????????????? ???D.?10cm
9. 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( ??) A.?米2???????? ?B.?米2???? ?? C.?(4+ )米2????? ? D.?(4+4tanθ)米2
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA= ,则下列结论:①DE=3cm;②EB=1cm;③=15cm2 正确的个数为(??? ) A.3个??????? B.2个???????????? C.1个?????????????? D.0个
二、填空题(共8题;共24分)
11. 计算:(π﹣3.14)0+2cos60°=________.
12. 在△ABC中,∠C=90°,若tanA= ,则sinB=________.
13. 在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin ?=________
14. 已知一个斜坡的坡度i=1:, 那么该斜坡的坡角的度数是________?度.
15. 已知<cosA<sin70°,则锐角A的取值范围是________?
16. 如图,在正方形ABCD中,AD= ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为________. 17. 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为________米. 18. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为________米.
三、计算题(共2题;共12分)
19. ( 6分 ) 计算:
20. ( 6分 ) 先化简,再求代数式 的值,其中m=2cos30°-tan45°
四、解答题(共4题;共32分)
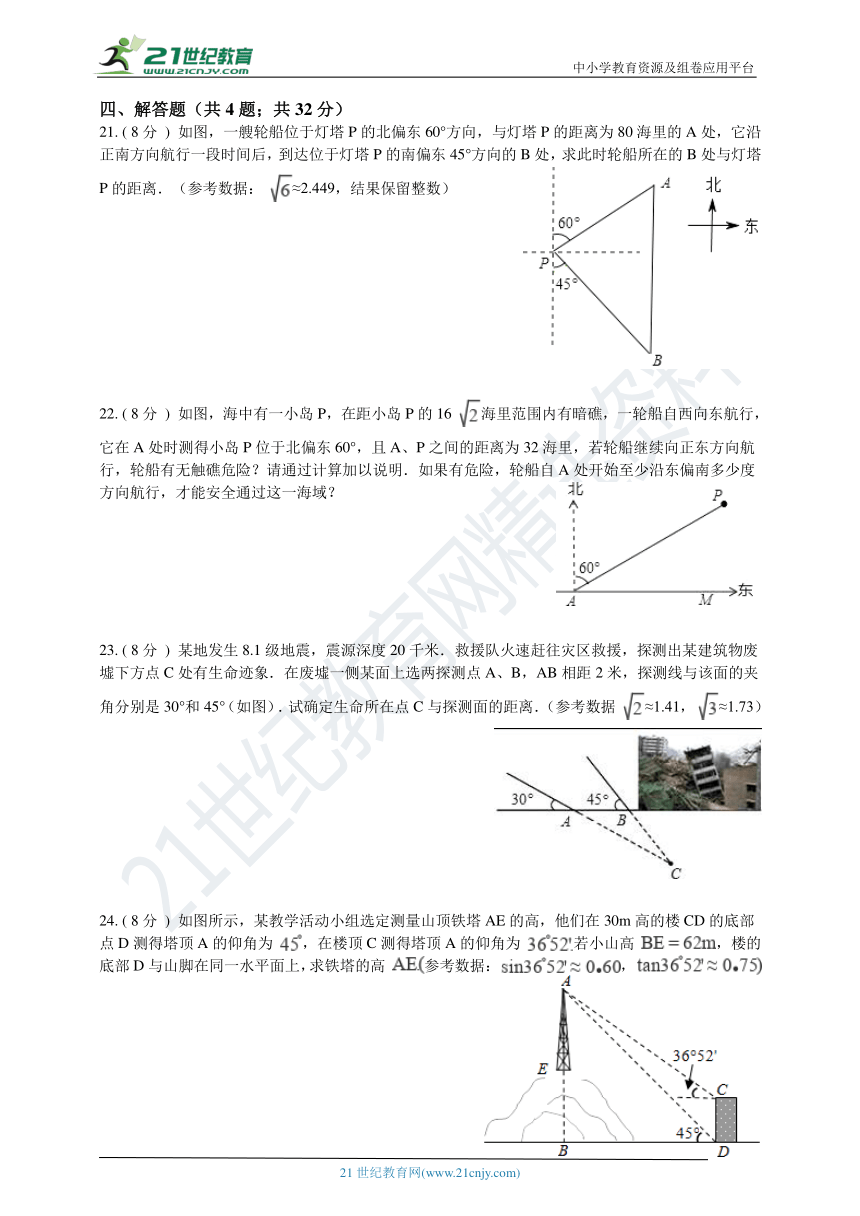
21. ( 8分 ) 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
22. ( 8分 ) 如图,海中有一小岛P,在距小岛P的16 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
23. ( 8分 ) 某地发生8.1级地震,震源深度20千米.救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据 ≈1.41, ≈1.73)
24. ( 8分 ) 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为 ,在楼顶C测得塔顶A的仰角为 若小山高 ,楼的底部D与山脚在同一水平面上,求铁塔的高 参考数据: ,
五、综合题(共2题;共22分)
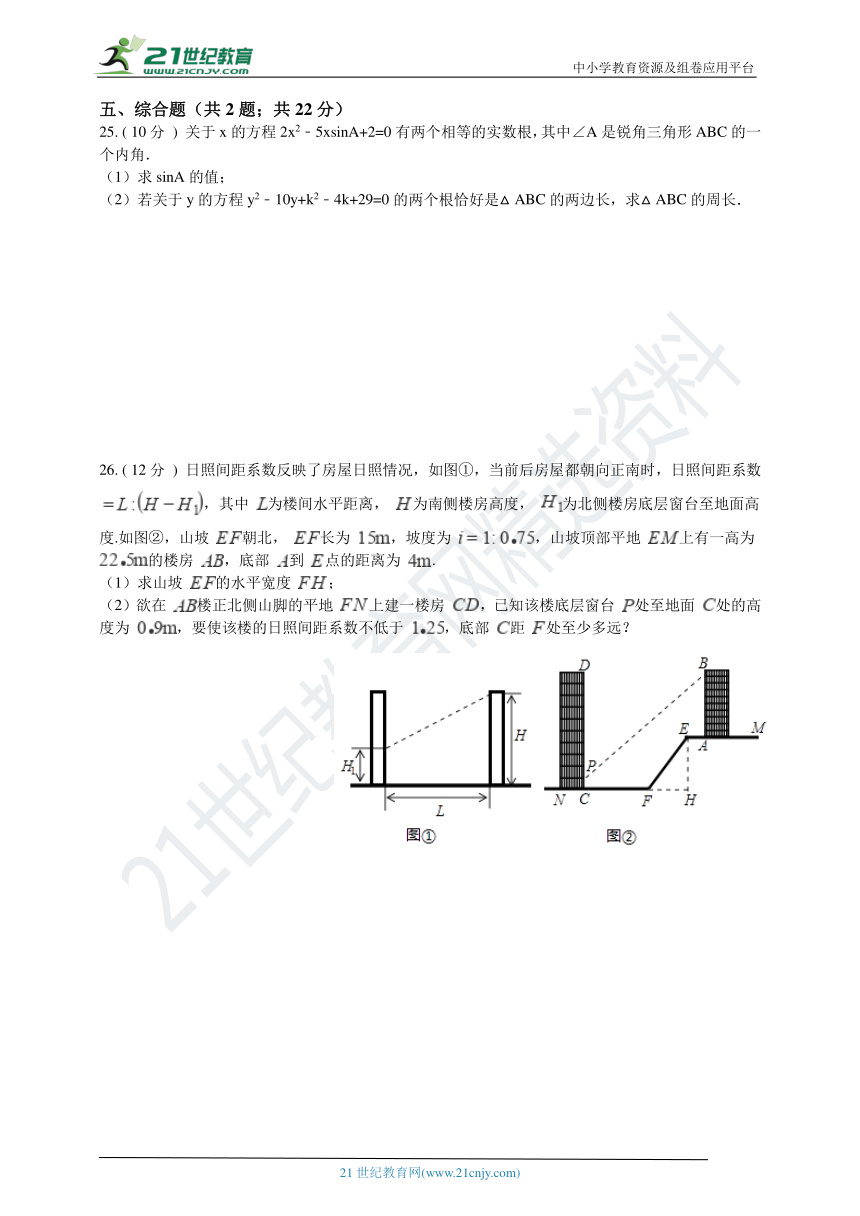
25. ( 10分 ) 关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
(1)求sinA的值;
(2)若关于y的方程y2﹣10y+k2﹣4k+29=0的两个根恰好是△ABC的两边长,求△ABC的周长.
26. ( 12分 ) 日照间距系数反映了房屋日照情况,如图①,当前后房屋都朝向正南时,日照间距系数 ,其中 为楼间水平距离, 为南侧楼房高度, 为北侧楼房底层窗台至地面高度.如图②,山坡 朝北, 长为 ,坡度为 ,山坡顶部平地 上有一高为 的楼房 ,底部 到 点的距离为 .
(1)求山坡 的水平宽度 ;
(2)欲在 楼正北侧山脚的平地 上建一楼房 ,已知该楼底层窗台 处至地面 处的高度为 ,要使该楼的日照间距系数不低于 ,底部 距 处至少多远?
答案解析部分
一、单选题
1.【答案】D
【考点】锐角三角函数的定义
【解析】【解答】解:如图所示: cosB= . 故答案为:D. 【分析】根据余弦函数的定义即可直接得出答案。
2.【答案】B
【考点】互余两角三角函数的关系
【解析】【解答】解:∵sin35°=cosα, ∴α=90°﹣35°=55°. 故选B. 【分析】根据锐角三角函数的概念,可以证明:一个角的正弦值等于它的余角的余弦值.
3.【答案】B
【考点】互余两角三角函数的关系
【解析】【解答】∵在△ABC中,∠C=90°, ∴∠A+∠B=90°, ∴sinA=cosB= . 故答案为:B. 【分析】根据直角三角形的两锐角互余得出∠A+∠B=90°,根据,互余两角,其中一个的正弦值,等于另一个的余弦值,即可得出答案。
4.【答案】B
【考点】锐角三角函数的增减性,特殊角的三角函数值
【解析】【解答】解:由正弦函数随角的增大而增大,余弦函数随角的增大而减小,得 30°<α<60°, 故选:B. 【分析】根据特殊角三角函数值,锐角函数的增减性,可得答案.
5.【答案】B
【考点】锐角三角函数的定义
【解析】【解答】如图, A、sinA= ,所以BC= ,故A不符合题意; B、cosA= ,所以 ,故B符合题意; C、tanA= ,所以BC=btanA,故C不符合题意; D、cotA= ,所以 BCcotA,故D不符合题意. 故答案为:B. 【分析】根据锐角函数的定义,正弦函数等于对边比斜边;余弦函数等于邻边比斜边;正切函数等于对边比邻边;余切函数等于邻边比对边;即可一一得出答案。
6.【答案】B
【考点】三角形内角和定理,特殊角的三角函数值
【解析】【解答】解:由题意得:∠A=45°,∠B=45°,∴∠C=180°﹣∠A﹣∠B=90°.故答案为:B. 【分析】由特殊角的锐角三角函数值可得∠A=45°,∠B=45°,再由三角形内角和定理可得∠C=180°﹣∠A﹣∠B=90°。
7.【答案】D
【考点】特殊角的三角函数值
【解析】【解答】∵△ABC中,∠A,∠B均为锐角,且(tanB﹣ )(2sinA﹣ )=0, ∴tanB﹣ =0或2sinA﹣ =0, 即tanB= 或sinA= . ∴∠B=60°或∠A=60°. ∴△ABC有一个角是60°. 故答案为:D.
【分析】根据两个因式的积0,则这两个因式至少有一个因式为0可得tanB-=0或2sinA-=0,解得tanB= ,或sinA= ,因为△ABC中,∠A,∠B均为锐角,由特殊角的锐角三角函数可得∠B=60°或∠A=60°.所以△ABC有一个角是60°.
8.【答案】A
【考点】线段垂直平分线的性质,解直角三角形
【解析】【解答】解:∵MN为AB的中垂线, ∴BD=AD. 设AD=acm, ∴BD=acm,CD=(16﹣a)cm, ∴cos∠BDC= , ∴a=10. ∴在Rt△BCD中,CD=6cm,BD=10cm, ∴BC=8cm. 故答案为:A. 【分析】利用垂直平分线的性质可得BD=AD,设AD=acm,则CD=(16-a)cm,由cos∠BDC=CD:BD,可求出a的值,再由勾股定理可得BC的值.
9.【答案】D
【考点】解直角三角形的应用
【解析】【解答】解:在Rt△ABC中,BC=AC?tanθ=4tanθ(米), ∴AC+BC=4+4tanθ(米), ∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2); 故答案为:D. 【分析】根据解直角三角形中正切的定义,得到BC=AC?tanθ,求出地毯的面积的表达式.
10.【答案】A.
【考点】菱形的性质,解直角三角形,平行四边形的面积
【解析】【解答】由题意可得,菱形的边长为5cm,又cosA= ,所以AE=4, 则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2 , 故答案为:A. 【分析】根据菱形的四边都相等可得菱形的边长为5cm,在直角三角形ADE中,由cosA=,求得AE的值;再由勾股定理可得DE;S菱形ABCD=ABDE=5×3=15cm2。
二、填空题
11.【答案】2
【考点】实数的运算,特殊角的三角函数值
【解析】【解答】原式=1+2× , =1+1, =2. 故答案为:2. 【分析】根据0指数的意义,特殊锐角三角函数值分别化简,再按有理数的混合运算顺序算出答案。
12.【答案】
【考点】勾股定理,锐角三角函数的定义
【解析】【解答】解:如图所示: ∵∠C=90°,tanA= , ∴设BC=x,则AC=2x,故AB= x, 则sinB= . 故答案为: ?. 【分析】根据正切函数的定义由tanA=?, 设BC=x,则AC=2x,根据勾股定理表示出AB的长,再根据正弦函数的定义即可得出答案。
13.【答案】
【考点】锐角三角函数的定义,特殊角的三角函数值
【解析】【解答】∵sinA= = , ∴∠A=60°, ∴ =30°, ∴sin =sin30°= . 故答案为: . 【分析】根据正弦函数的定义,求出sinA的值,根据特殊锐角的三角函数值求出∠A的度数,进而得出∠A一半的度数,根据特殊锐角函数值即可得出答案。
14.【答案】30
【考点】解直角三角形的应用
【解析】【解答】解:∵tanα=1:= , ∴坡角=30°. 【分析】坡度=坡角的正切值,据此直接解答.
15.【答案】20°<∠A<30°
【考点】锐角三角函数的增减性
【解析】【解答】解:∵<cosA<sin70°,sin70°=cos20°, ∴cos30°<cosA<cos20°, ∴20°<∠A<30°. 故答案为:20°<∠A<30°. 【分析】利用特殊角的三角函数值以及互余两角的锐角三角函数关系得出∠A的取值范围.
16.【答案】
【考点】三角形的面积,等边三角形的判定与性质,正方形的性质,解直角三角形
【解析】【解答】如图, ∵四边形ABCD是正方形,∴∠ABC=90°,∵把边BC绕点B逆时针旋转30°得到线段BP,∴PB=BC=AB,∠PBC=30°,∴∠ABP=60°,∴△ABP是等边三角形,∴∠BAP=60°,AP=AB= ,∵AD= ,∴AE=4,DE=2,∴CE= ﹣2,PE=4﹣ ,过P作PF⊥CD于F,∴PF= PE= ﹣3,∴三角形PCE的面积= CE?PF= ×( ﹣2)×( ﹣3)= ,故答案为: . 【分析】过P作PF⊥CD于F,由旋转的长性质可得PB=BC=AB,根据旋转角为30°何正方形的性质可得∠ABP=60°,于是可得△ABP是等边三角形,则∠BAP=60°=∠AED,AP=AB,解直角三角形ADE可得AE和DE的长,则CE=CD-DE,PE=AE-AP,解直角三角形PEF可求得PF的长,所以可得三角形PCE的面积=CE?PF.
17.【答案】
【考点】解直角三角形的应用
【解析】【解答】解:在Rt△BCD中,∵tan∠CBD= , ∴BD= , 在Rt△ACD中,∵tan∠A= = , ∴tanα= , 解得:CD= , 故答案为: . 【分析】在Rt△BCD中有BD= ,在Rt△ACD中,根据tan∠A= = 可得tanα= ,解之求出CD即可得.
18.【答案】14+2
【考点】相似三角形的判定与性质,解直角三角形
【解析】【解答】如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E. ∵∠DCE=30°,CD=8米, ∴CE=CDcos∠DCE=8× (米), ∴DE=4米, 设AB=x,EF=y, ∵DE⊥BF,AB⊥BF, ∴△DEF∽△ABF, ∴ ,即 ①, ∵1米杆的影长为2米,根据同一时间物高与影长成正比可得, = …②, ①②联立,解得x=14+2 (米). 【分析】这是一道解直角三角形的应用型问题,所以先将图形补充完整。延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.在直角三角形CDE中,用∠DCE的余弦可求得CE的长,则DE的长可求,设AB=x,EF=y,由题意易得△DEF∽△ABF,则可得比例式,,代入则可得关于x、y的方程;再根据同一时间物高与影长成正比又可得关于x、y的方程;联立解方程组即可得到电线杆的高度。
三、计算题
19.【答案】解:原式=﹣3﹣2 + ﹣1+ ﹣1=﹣5
【考点】实数的运算,特殊角的三角函数值
【解析】【分析】根据负指数的意义,二次根式的性质,0指数的意义,绝对值的意义,特殊锐角三角函数值,分别化简,再根据实数的运算算出结果。
20.【答案】解:原式= = = = 当m= = 时,原式=
【考点】利用分式运算化简求值,特殊角的三角函数值
【解析】【分析】将分式进行化简,先将括号内的进行通分化简,然后再将除法转变为乘法,化成最简分式,最后将特殊的锐角三角函数的值带入即可.
四、解答题
21.【答案】解:作PC⊥AB交于C点, 由题意可得∠APC=30°,∠BPC=45°,AP=80(海里). 在Rt△APC中,PC=PA?cos∠APC=40 (海里). 在Rt△PCB中,PB= ≈98(海里). 答:此时轮船所在的B处与灯塔P的距离是98海里.
【考点】解直角三角形的应用﹣方向角问题
【解析】【分析】构造直角三角形,作PC⊥AB交于C点;由方位角易知∠APC=30°,∠BPC=45°,则根据解直角三角形的知识解答即可.
22.【答案】解:过P作PB⊥AM于B, 在Rt△APB中,∵∠PAB=30°, ∴PB= AP= ×32=16海里, ∵16<16 故轮船有触礁危险, 为了安全,应该变航行方向,并且保证点P到航线的距离不小于暗礁的半径16 海里,即这个距离至少为16 海里, 设安全航向为AC,作PD⊥AC于点D, ? 由题意得,AP=32海里,PD=16 海里, ∵sin∠PAC= , ∴在Rt△PAD中,∠PAC=45°, ∴∠BAC=∠PAC-∠PAB=45°-30°=15°, 答:轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
【考点】含30度角的直角三角形,解直角三角形
【解析】【分析】先解直角三角形ABP求得PB的值,小于,故轮船有触礁危险;再作出改变航向后的图形,且点P到航向AC的距离PD=,求得∠BAC的度数即可说明轮船自A处如何改变航向才能安全通过这一海域.
23.【答案】解:过C作CD⊥AB, 设CD=x米, ∵∠ABE=45°, ∴∠CBD=45°, ∴DB=CD=x米, ∵∠CAD=30°, ∴AD= ?CD= x米, ∵AB相距2米, ∴ x﹣x=2, 解得:x= ?. 答:生命所在点C与探测面的距离是 米.
【考点】解直角三角形的应用
【解析】【分析】过C作CD⊥AB,设CD=x米,根据等腰直角三角形的性质得出DB=CD=x米,根据含30°直角三角形的边之间的关系得出AD=CD=?x,然后根据AB=AD-BD即可列出方程,求解即可。
24.【答案】解:如图,过点C作 于点F, 设塔高 ,作 于点F, 则四边形BDCF是矩形, , , ∴EF=BE-BF=62-30=32, 在 中, , , 在 中, , , , , , 答:该铁塔的高AE约为58米
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】设塔高? AE = x ?,作? CF ⊥ AB ?于点F,根据楼高和山高可求出EF , 继而得出AF,在Rt△AFC中表示出CF,在Rt△ABF中由tan∠ACF=AE:CF,从而求出AE的值.
五、综合题
25.【答案】(1)解:根据题意得△=25sin2A-16=0, ∴sin2A= , ∴sinA=± , ∵∠A为锐角, ∴sinA= (2)解:由题意知,方程y2-10y+k2-4k+29=0有两个实数根, 则△≥0, ∴100-4(k2-4k+29)≥0, ∴-(k-2)2≥0, ∴(k-2)2≤0, 又∵(k-2)2≥0, ∴k=2, 把k=2代入方程,得y2-10y+25=0, 解得y1=y2=5,∴△ABC是等腰三角形,且腰长为5. 分两种情况: 当∠A是顶角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5, ∵sinA= , ∴AD=3,BD=4∴DC=2, ∴BC=2 . ∴△ABC的周长为10+2 ; 当∠A是底角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=5, ∵sinA= , ∴AD=DC=3, ∴AC=6. ∴△ABC的周长为16, 综合以上讨论可知:△ABC的周长为10+2 或16.
【考点】一元二次方程根的判别式及应用,锐角三角函数的定义
【解析】【分析】(1)根据一元二次方程有两个相等的实数根知其根的判别式等于0,从而得出方程求出并根据实际情况得出sinA的值; (2)由题意知,方程y2-10y+k2-4k+29=0有两个实数根,故则△≥0,从而得出不等式,根据偶次方的非负性从而求解得出k的值,把k的值代入原方程求解得出y的值,从而判断出△ABC是等腰三角形,且腰长为5.分两种情况:当∠A是顶角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5,根据锐角三角函数的定义及sinA的值,求出BC的长,根据三角形周长的计算方法得出答案;当∠A是底角时:如图,过点B作BD⊥AC于点D,根据锐角三角函数的定义及sinA的值等腰三角形的三线合一求出AC的长,根据三角形周长的计算方法得出答案;
26.【答案】(1)解:∵EF的坡度i=1:0.75=4:3∴EH:FH=4:3 在Rt△EFH中,EF2=EH2+FH2 即16x2+9x2=25x2=152 解之:x=3 ∴FH=9,EH=12 答:山坡 的水平宽度 的长为9m。 (2)解:延长BA、FH,两延长线交于点G, ∵EH=12,AB=22.5 ∴AG=EH=12,AE=HG=4 ∴L=CG=CF+FH+HG=CF+13 BG=AB+AG=22.5+12=34.5 ∴(CF+13):(BG-PC)≥1.25 即(CF+13):(34.5-0.9)≥1.25 解之:CF≥29 CF取最小整数 ∴CF=29
【考点】勾股定理,解直角三角形的应用﹣坡度坡角问题
【解析】【分析】(1)根据EF的坡度,可得出EH:FH=4:3,再利用勾股定理,建立方程求解即可。(2)根据题意添加辅助线,延长BA、FH,两延长线交于点G,根据矩形的性质,可得出AG=EH=12,AE=HG=4,再求出L=13+CF及BG的长,根据该楼的日照间距系数(日照间距系数 )≥ ,建立不等式,求出不等式的最小整数解即可。
考试时间:120分钟 满分:120分 姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1. 在△ABC中,∠C=90°,如果AB=6,BC=3,那么cosB的值是(?? )
A.??????????????????????????????????????? B.?????????????????????????????????????? C.?????????????????????????????????????? D.?
2. 已知sin35°=cosα,则α为(???? )
A.?35°????????????????????????????????????? ??B.?55°???????????????????????????????????????C.?75°???????????????????????????? ???????????D.?65°
3. 在 中, , 若cosB= ,则sinA的值为 (?? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
4. 若锐角α满足sinα> ,且cosα> ,则α的范围是(?? )
A.?0°<α<30°????????????????????B.?30°<α<60°????????????????????C.?60°<α<90°????????????????????D.?45°<α<90°
5. 在Rt△ABC中, , , ,下列选项中一定正确的是( ??)
A.?;????????????????? B.?;???????????????? C.?;????????????????? D.?.
6. 在△ABC中,∠A,∠B都是锐角,tanA=1,sinB= ,你认为△ABC最确切的判断是(??? )
A.?等腰三角形?????????????????? B.?等腰直角三角形?????????????????? C.?直角三角形??????????????????? D.?锐角三角形
7. △ABC中,∠A,∠B均为锐角,且(tanB﹣ )(2sinA﹣ )=0,则△ABC一定是(?? )
A.等腰三角形 B.等边三角形 C.直角三角形 D.有一个角是60°的三角形
8. 如图,△ABC中,∠C=90°,AC=16cm,AB的中垂线MN交AC于点D,连接BD,若cos∠BDC= ?,则BC=(?? ) A.?8cm??????????????????? ?B.?4cm???????????????????? ?C.?6cm?????????????????????? ???D.?10cm
9. 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( ??) A.?米2???????? ?B.?米2???? ?? C.?(4+ )米2????? ? D.?(4+4tanθ)米2
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA= ,则下列结论:①DE=3cm;②EB=1cm;③=15cm2 正确的个数为(??? ) A.3个??????? B.2个???????????? C.1个?????????????? D.0个
二、填空题(共8题;共24分)
11. 计算:(π﹣3.14)0+2cos60°=________.
12. 在△ABC中,∠C=90°,若tanA= ,则sinB=________.
13. 在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin ?=________
14. 已知一个斜坡的坡度i=1:, 那么该斜坡的坡角的度数是________?度.
15. 已知<cosA<sin70°,则锐角A的取值范围是________?
16. 如图,在正方形ABCD中,AD= ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为________. 17. 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为________米. 18. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为________米.
三、计算题(共2题;共12分)
19. ( 6分 ) 计算:
20. ( 6分 ) 先化简,再求代数式 的值,其中m=2cos30°-tan45°
四、解答题(共4题;共32分)
21. ( 8分 ) 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
22. ( 8分 ) 如图,海中有一小岛P,在距小岛P的16 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
23. ( 8分 ) 某地发生8.1级地震,震源深度20千米.救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据 ≈1.41, ≈1.73)
24. ( 8分 ) 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为 ,在楼顶C测得塔顶A的仰角为 若小山高 ,楼的底部D与山脚在同一水平面上,求铁塔的高 参考数据: ,
五、综合题(共2题;共22分)
25. ( 10分 ) 关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
(1)求sinA的值;
(2)若关于y的方程y2﹣10y+k2﹣4k+29=0的两个根恰好是△ABC的两边长,求△ABC的周长.
26. ( 12分 ) 日照间距系数反映了房屋日照情况,如图①,当前后房屋都朝向正南时,日照间距系数 ,其中 为楼间水平距离, 为南侧楼房高度, 为北侧楼房底层窗台至地面高度.如图②,山坡 朝北, 长为 ,坡度为 ,山坡顶部平地 上有一高为 的楼房 ,底部 到 点的距离为 .
(1)求山坡 的水平宽度 ;
(2)欲在 楼正北侧山脚的平地 上建一楼房 ,已知该楼底层窗台 处至地面 处的高度为 ,要使该楼的日照间距系数不低于 ,底部 距 处至少多远?
答案解析部分
一、单选题
1.【答案】D
【考点】锐角三角函数的定义
【解析】【解答】解:如图所示: cosB= . 故答案为:D. 【分析】根据余弦函数的定义即可直接得出答案。
2.【答案】B
【考点】互余两角三角函数的关系
【解析】【解答】解:∵sin35°=cosα, ∴α=90°﹣35°=55°. 故选B. 【分析】根据锐角三角函数的概念,可以证明:一个角的正弦值等于它的余角的余弦值.
3.【答案】B
【考点】互余两角三角函数的关系
【解析】【解答】∵在△ABC中,∠C=90°, ∴∠A+∠B=90°, ∴sinA=cosB= . 故答案为:B. 【分析】根据直角三角形的两锐角互余得出∠A+∠B=90°,根据,互余两角,其中一个的正弦值,等于另一个的余弦值,即可得出答案。
4.【答案】B
【考点】锐角三角函数的增减性,特殊角的三角函数值
【解析】【解答】解:由正弦函数随角的增大而增大,余弦函数随角的增大而减小,得 30°<α<60°, 故选:B. 【分析】根据特殊角三角函数值,锐角函数的增减性,可得答案.
5.【答案】B
【考点】锐角三角函数的定义
【解析】【解答】如图, A、sinA= ,所以BC= ,故A不符合题意; B、cosA= ,所以 ,故B符合题意; C、tanA= ,所以BC=btanA,故C不符合题意; D、cotA= ,所以 BCcotA,故D不符合题意. 故答案为:B. 【分析】根据锐角函数的定义,正弦函数等于对边比斜边;余弦函数等于邻边比斜边;正切函数等于对边比邻边;余切函数等于邻边比对边;即可一一得出答案。
6.【答案】B
【考点】三角形内角和定理,特殊角的三角函数值
【解析】【解答】解:由题意得:∠A=45°,∠B=45°,∴∠C=180°﹣∠A﹣∠B=90°.故答案为:B. 【分析】由特殊角的锐角三角函数值可得∠A=45°,∠B=45°,再由三角形内角和定理可得∠C=180°﹣∠A﹣∠B=90°。
7.【答案】D
【考点】特殊角的三角函数值
【解析】【解答】∵△ABC中,∠A,∠B均为锐角,且(tanB﹣ )(2sinA﹣ )=0, ∴tanB﹣ =0或2sinA﹣ =0, 即tanB= 或sinA= . ∴∠B=60°或∠A=60°. ∴△ABC有一个角是60°. 故答案为:D.
【分析】根据两个因式的积0,则这两个因式至少有一个因式为0可得tanB-=0或2sinA-=0,解得tanB= ,或sinA= ,因为△ABC中,∠A,∠B均为锐角,由特殊角的锐角三角函数可得∠B=60°或∠A=60°.所以△ABC有一个角是60°.
8.【答案】A
【考点】线段垂直平分线的性质,解直角三角形
【解析】【解答】解:∵MN为AB的中垂线, ∴BD=AD. 设AD=acm, ∴BD=acm,CD=(16﹣a)cm, ∴cos∠BDC= , ∴a=10. ∴在Rt△BCD中,CD=6cm,BD=10cm, ∴BC=8cm. 故答案为:A. 【分析】利用垂直平分线的性质可得BD=AD,设AD=acm,则CD=(16-a)cm,由cos∠BDC=CD:BD,可求出a的值,再由勾股定理可得BC的值.
9.【答案】D
【考点】解直角三角形的应用
【解析】【解答】解:在Rt△ABC中,BC=AC?tanθ=4tanθ(米), ∴AC+BC=4+4tanθ(米), ∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2); 故答案为:D. 【分析】根据解直角三角形中正切的定义,得到BC=AC?tanθ,求出地毯的面积的表达式.
10.【答案】A.
【考点】菱形的性质,解直角三角形,平行四边形的面积
【解析】【解答】由题意可得,菱形的边长为5cm,又cosA= ,所以AE=4, 则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2 , 故答案为:A. 【分析】根据菱形的四边都相等可得菱形的边长为5cm,在直角三角形ADE中,由cosA=,求得AE的值;再由勾股定理可得DE;S菱形ABCD=ABDE=5×3=15cm2。
二、填空题
11.【答案】2
【考点】实数的运算,特殊角的三角函数值
【解析】【解答】原式=1+2× , =1+1, =2. 故答案为:2. 【分析】根据0指数的意义,特殊锐角三角函数值分别化简,再按有理数的混合运算顺序算出答案。
12.【答案】
【考点】勾股定理,锐角三角函数的定义
【解析】【解答】解:如图所示: ∵∠C=90°,tanA= , ∴设BC=x,则AC=2x,故AB= x, 则sinB= . 故答案为: ?. 【分析】根据正切函数的定义由tanA=?, 设BC=x,则AC=2x,根据勾股定理表示出AB的长,再根据正弦函数的定义即可得出答案。
13.【答案】
【考点】锐角三角函数的定义,特殊角的三角函数值
【解析】【解答】∵sinA= = , ∴∠A=60°, ∴ =30°, ∴sin =sin30°= . 故答案为: . 【分析】根据正弦函数的定义,求出sinA的值,根据特殊锐角的三角函数值求出∠A的度数,进而得出∠A一半的度数,根据特殊锐角函数值即可得出答案。
14.【答案】30
【考点】解直角三角形的应用
【解析】【解答】解:∵tanα=1:= , ∴坡角=30°. 【分析】坡度=坡角的正切值,据此直接解答.
15.【答案】20°<∠A<30°
【考点】锐角三角函数的增减性
【解析】【解答】解:∵<cosA<sin70°,sin70°=cos20°, ∴cos30°<cosA<cos20°, ∴20°<∠A<30°. 故答案为:20°<∠A<30°. 【分析】利用特殊角的三角函数值以及互余两角的锐角三角函数关系得出∠A的取值范围.
16.【答案】
【考点】三角形的面积,等边三角形的判定与性质,正方形的性质,解直角三角形
【解析】【解答】如图, ∵四边形ABCD是正方形,∴∠ABC=90°,∵把边BC绕点B逆时针旋转30°得到线段BP,∴PB=BC=AB,∠PBC=30°,∴∠ABP=60°,∴△ABP是等边三角形,∴∠BAP=60°,AP=AB= ,∵AD= ,∴AE=4,DE=2,∴CE= ﹣2,PE=4﹣ ,过P作PF⊥CD于F,∴PF= PE= ﹣3,∴三角形PCE的面积= CE?PF= ×( ﹣2)×( ﹣3)= ,故答案为: . 【分析】过P作PF⊥CD于F,由旋转的长性质可得PB=BC=AB,根据旋转角为30°何正方形的性质可得∠ABP=60°,于是可得△ABP是等边三角形,则∠BAP=60°=∠AED,AP=AB,解直角三角形ADE可得AE和DE的长,则CE=CD-DE,PE=AE-AP,解直角三角形PEF可求得PF的长,所以可得三角形PCE的面积=CE?PF.
17.【答案】
【考点】解直角三角形的应用
【解析】【解答】解:在Rt△BCD中,∵tan∠CBD= , ∴BD= , 在Rt△ACD中,∵tan∠A= = , ∴tanα= , 解得:CD= , 故答案为: . 【分析】在Rt△BCD中有BD= ,在Rt△ACD中,根据tan∠A= = 可得tanα= ,解之求出CD即可得.
18.【答案】14+2
【考点】相似三角形的判定与性质,解直角三角形
【解析】【解答】如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E. ∵∠DCE=30°,CD=8米, ∴CE=CDcos∠DCE=8× (米), ∴DE=4米, 设AB=x,EF=y, ∵DE⊥BF,AB⊥BF, ∴△DEF∽△ABF, ∴ ,即 ①, ∵1米杆的影长为2米,根据同一时间物高与影长成正比可得, = …②, ①②联立,解得x=14+2 (米). 【分析】这是一道解直角三角形的应用型问题,所以先将图形补充完整。延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.在直角三角形CDE中,用∠DCE的余弦可求得CE的长,则DE的长可求,设AB=x,EF=y,由题意易得△DEF∽△ABF,则可得比例式,,代入则可得关于x、y的方程;再根据同一时间物高与影长成正比又可得关于x、y的方程;联立解方程组即可得到电线杆的高度。
三、计算题
19.【答案】解:原式=﹣3﹣2 + ﹣1+ ﹣1=﹣5
【考点】实数的运算,特殊角的三角函数值
【解析】【分析】根据负指数的意义,二次根式的性质,0指数的意义,绝对值的意义,特殊锐角三角函数值,分别化简,再根据实数的运算算出结果。
20.【答案】解:原式= = = = 当m= = 时,原式=
【考点】利用分式运算化简求值,特殊角的三角函数值
【解析】【分析】将分式进行化简,先将括号内的进行通分化简,然后再将除法转变为乘法,化成最简分式,最后将特殊的锐角三角函数的值带入即可.
四、解答题
21.【答案】解:作PC⊥AB交于C点, 由题意可得∠APC=30°,∠BPC=45°,AP=80(海里). 在Rt△APC中,PC=PA?cos∠APC=40 (海里). 在Rt△PCB中,PB= ≈98(海里). 答:此时轮船所在的B处与灯塔P的距离是98海里.
【考点】解直角三角形的应用﹣方向角问题
【解析】【分析】构造直角三角形,作PC⊥AB交于C点;由方位角易知∠APC=30°,∠BPC=45°,则根据解直角三角形的知识解答即可.
22.【答案】解:过P作PB⊥AM于B, 在Rt△APB中,∵∠PAB=30°, ∴PB= AP= ×32=16海里, ∵16<16 故轮船有触礁危险, 为了安全,应该变航行方向,并且保证点P到航线的距离不小于暗礁的半径16 海里,即这个距离至少为16 海里, 设安全航向为AC,作PD⊥AC于点D, ? 由题意得,AP=32海里,PD=16 海里, ∵sin∠PAC= , ∴在Rt△PAD中,∠PAC=45°, ∴∠BAC=∠PAC-∠PAB=45°-30°=15°, 答:轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
【考点】含30度角的直角三角形,解直角三角形
【解析】【分析】先解直角三角形ABP求得PB的值,小于,故轮船有触礁危险;再作出改变航向后的图形,且点P到航向AC的距离PD=,求得∠BAC的度数即可说明轮船自A处如何改变航向才能安全通过这一海域.
23.【答案】解:过C作CD⊥AB, 设CD=x米, ∵∠ABE=45°, ∴∠CBD=45°, ∴DB=CD=x米, ∵∠CAD=30°, ∴AD= ?CD= x米, ∵AB相距2米, ∴ x﹣x=2, 解得:x= ?. 答:生命所在点C与探测面的距离是 米.
【考点】解直角三角形的应用
【解析】【分析】过C作CD⊥AB,设CD=x米,根据等腰直角三角形的性质得出DB=CD=x米,根据含30°直角三角形的边之间的关系得出AD=CD=?x,然后根据AB=AD-BD即可列出方程,求解即可。
24.【答案】解:如图,过点C作 于点F, 设塔高 ,作 于点F, 则四边形BDCF是矩形, , , ∴EF=BE-BF=62-30=32, 在 中, , , 在 中, , , , , , 答:该铁塔的高AE约为58米
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】设塔高? AE = x ?,作? CF ⊥ AB ?于点F,根据楼高和山高可求出EF , 继而得出AF,在Rt△AFC中表示出CF,在Rt△ABF中由tan∠ACF=AE:CF,从而求出AE的值.
五、综合题
25.【答案】(1)解:根据题意得△=25sin2A-16=0, ∴sin2A= , ∴sinA=± , ∵∠A为锐角, ∴sinA= (2)解:由题意知,方程y2-10y+k2-4k+29=0有两个实数根, 则△≥0, ∴100-4(k2-4k+29)≥0, ∴-(k-2)2≥0, ∴(k-2)2≤0, 又∵(k-2)2≥0, ∴k=2, 把k=2代入方程,得y2-10y+25=0, 解得y1=y2=5,∴△ABC是等腰三角形,且腰长为5. 分两种情况: 当∠A是顶角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5, ∵sinA= , ∴AD=3,BD=4∴DC=2, ∴BC=2 . ∴△ABC的周长为10+2 ; 当∠A是底角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=5, ∵sinA= , ∴AD=DC=3, ∴AC=6. ∴△ABC的周长为16, 综合以上讨论可知:△ABC的周长为10+2 或16.
【考点】一元二次方程根的判别式及应用,锐角三角函数的定义
【解析】【分析】(1)根据一元二次方程有两个相等的实数根知其根的判别式等于0,从而得出方程求出并根据实际情况得出sinA的值; (2)由题意知,方程y2-10y+k2-4k+29=0有两个实数根,故则△≥0,从而得出不等式,根据偶次方的非负性从而求解得出k的值,把k的值代入原方程求解得出y的值,从而判断出△ABC是等腰三角形,且腰长为5.分两种情况:当∠A是顶角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5,根据锐角三角函数的定义及sinA的值,求出BC的长,根据三角形周长的计算方法得出答案;当∠A是底角时:如图,过点B作BD⊥AC于点D,根据锐角三角函数的定义及sinA的值等腰三角形的三线合一求出AC的长,根据三角形周长的计算方法得出答案;
26.【答案】(1)解:∵EF的坡度i=1:0.75=4:3∴EH:FH=4:3 在Rt△EFH中,EF2=EH2+FH2 即16x2+9x2=25x2=152 解之:x=3 ∴FH=9,EH=12 答:山坡 的水平宽度 的长为9m。 (2)解:延长BA、FH,两延长线交于点G, ∵EH=12,AB=22.5 ∴AG=EH=12,AE=HG=4 ∴L=CG=CF+FH+HG=CF+13 BG=AB+AG=22.5+12=34.5 ∴(CF+13):(BG-PC)≥1.25 即(CF+13):(34.5-0.9)≥1.25 解之:CF≥29 CF取最小整数 ∴CF=29
【考点】勾股定理,解直角三角形的应用﹣坡度坡角问题
【解析】【分析】(1)根据EF的坡度,可得出EH:FH=4:3,再利用勾股定理,建立方程求解即可。(2)根据题意添加辅助线,延长BA、FH,两延长线交于点G,根据矩形的性质,可得出AG=EH=12,AE=HG=4,再求出L=13+CF及BG的长,根据该楼的日照间距系数(日照间距系数 )≥ ,建立不等式,求出不等式的最小整数解即可。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
