必修2第二章 直线与平面平行的判定(课件)
文档属性
| 名称 | 必修2第二章 直线与平面平行的判定(课件) |

|
|
| 格式 | zip | ||
| 文件大小 | 743.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 14:40:48 | ||
图片预览



文档简介
2.2.1直线与平面
平行的判定
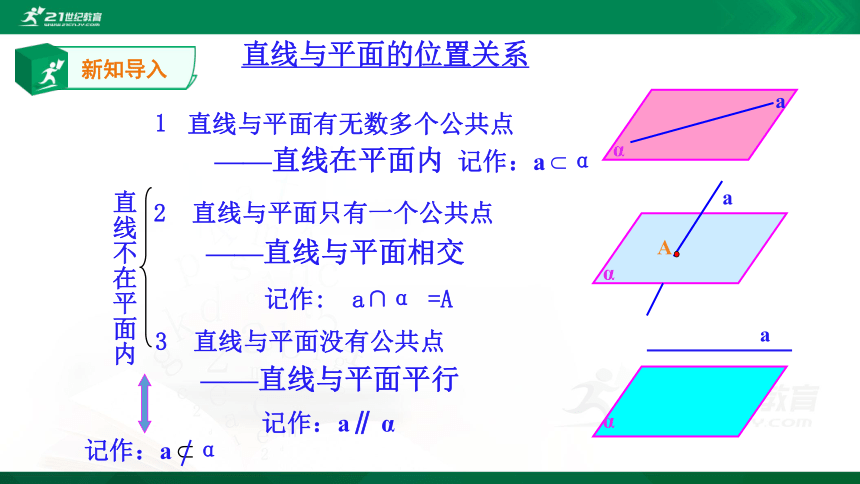
直线与平面的位置关系
——直线在平面内
2 直线与平面只有一个公共点
——直线与平面相交
记作: a∩α =A
3 直线与平面没有公共点
——直线与平面平行
记作:a∥ α
复习引入
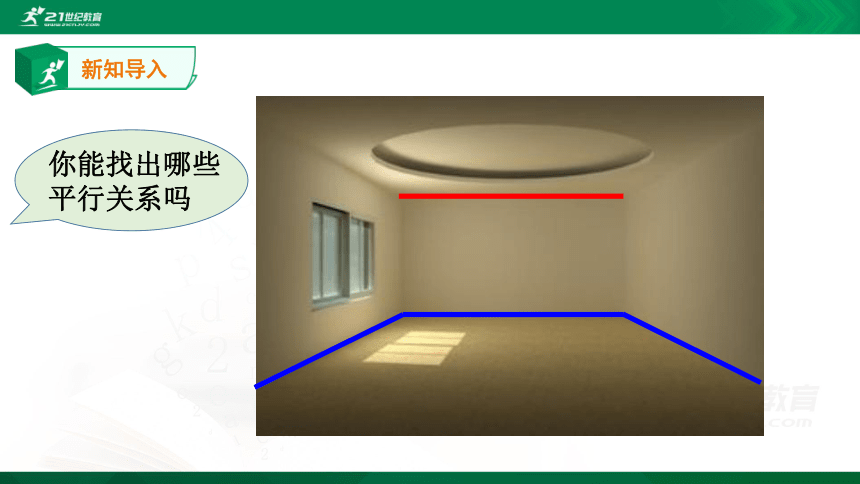
生活中的线面平行
生活中的线面平行
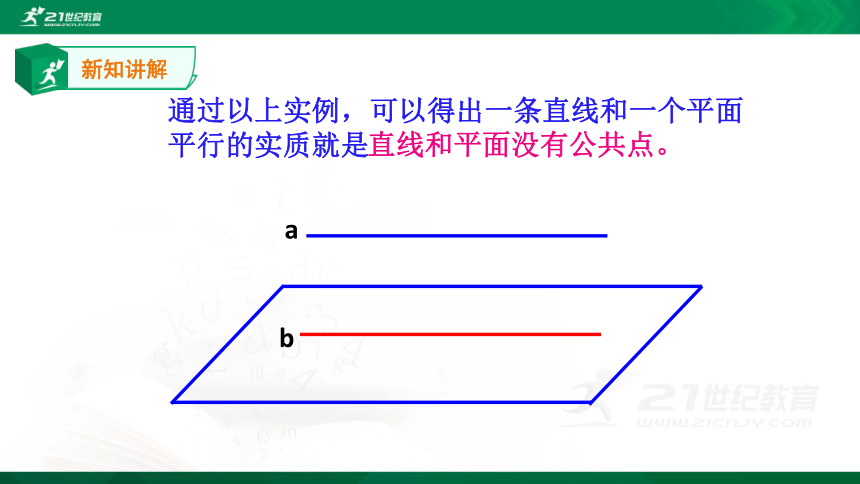
通过以上实例,可以得出一条直线和一个平面平行的实质就是
直线和平面没有公共点。
a
b
归纳总结
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行
直线与平面平行的判定定理
b
a
符号表示:
三者缺一不可!
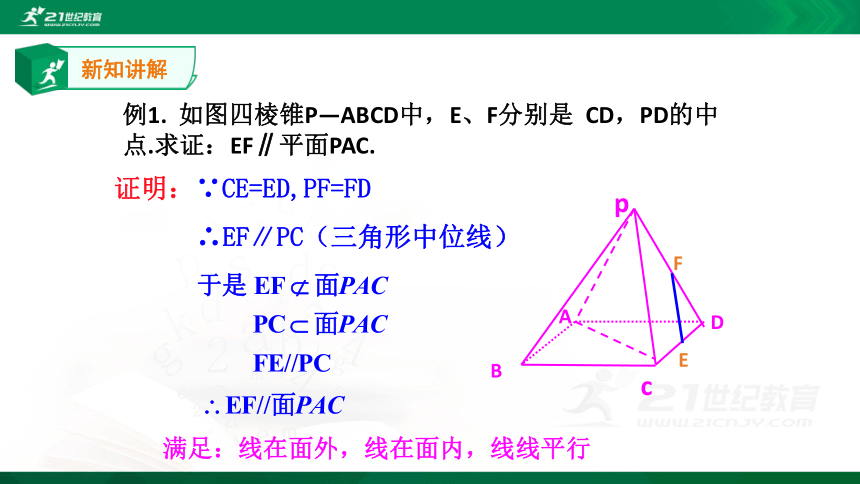
证明:∵CE=ED,PF=FD
∴EF∥PC(三角形中位线)
例1. 如图四棱锥P—ABCD中,E、F分别是 CD,PD的中点.求证:EF∥平面PAC.
A
B
D
E
F
课堂例题
c
p
满足:线在面外,线在面内,线线平行
例2.如图,四棱锥A—DBCE中,O为 底面正方形DBCE对角线的交点,F为AE上一动点. F在何位置 会有AB//平面DCF.
分析:连接OF,
可知F为
△ABE的边AE的中点时,AB//OF.
观察动态图
A
B
C
D
F
O
E
解:当F是AE中点时,满足题意
理由如下
连接OF,
∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,
1. 两个全等的正方形ABCD、ABEF不在同
一平面内,M、N是对角线AC、BF的中点
求证:MN ∥面BCE
分析:有两个中点一般考虑中位线
由M、N是中点知:
MN ∥ CE
课堂巩固
连接AE,CE
所以 MN ∥面BCE
证明:连接AE、CE,
∵点N为正方形ABEF对角线BF的中点
∴AE经过点N
又 点M为正方形ABCD 对角线AC的中点
∴ MN//CE
又
2.一木块儿如图所示,点P在平面VAC内,现在准备过点P把木块锯开,且截面与VB、AC平行,请问木工师傅该如何画出该截面与木块儿表面交线?
●
V
P
C
A
B
●
V
P
C
A
B
分析:本题是一道实际问题。要解决问题我们必须要建立必要的数学模型,而这个模型就是直线与平面平行的判定定理。
E
G
H
F
因为点P在表面,因此在表面要找到与VB 、 AC分别平行的线,且这些线在经过点P的同一平面内
●
V
P
C
A
E
G
F
解:在平面ACV 内过点P作直线HE∥AC,交VC、VA于点H、E;然后过点E作VB的平行线交AB于F
∵FE∩EH=E
∴FE、EH确定平面FEH,
H
B
∴AC ∥平面FEH
HE∥AC
反思1:要证明直线与平面平行可以运用判定定理;
反思2:运用定理时一定要注意满足三个条件:
反思3:运用定理的关键是找平行线;找平行线又经常
会用到三角形中位线定理.
“面外、面内、平行”
题后反思总结
1.证明直线与平面平行的方法:
(1)利用定义;
(2)利用判定定理.(关键找到三个条件)
2.数学思想方法:转化的思想
课堂小结
直线与平面没有公共点
两个全等的正方形ABCD、ABEF不在同
一平面内, M、N 是AC,BF上的点且AM=FN。
求证:MN ∥面BCE
课后作业
课本56页T2、63页T1
Q
P
平行的判定
直线与平面的位置关系
——直线在平面内
2 直线与平面只有一个公共点
——直线与平面相交
记作: a∩α =A
3 直线与平面没有公共点
——直线与平面平行
记作:a∥ α
复习引入
生活中的线面平行
生活中的线面平行
通过以上实例,可以得出一条直线和一个平面平行的实质就是
直线和平面没有公共点。
a
b
归纳总结
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行
直线与平面平行的判定定理
b
a
符号表示:
三者缺一不可!
证明:∵CE=ED,PF=FD
∴EF∥PC(三角形中位线)
例1. 如图四棱锥P—ABCD中,E、F分别是 CD,PD的中点.求证:EF∥平面PAC.
A
B
D
E
F
课堂例题
c
p
满足:线在面外,线在面内,线线平行
例2.如图,四棱锥A—DBCE中,O为 底面正方形DBCE对角线的交点,F为AE上一动点. F在何位置 会有AB//平面DCF.
分析:连接OF,
可知F为
△ABE的边AE的中点时,AB//OF.
观察动态图
A
B
C
D
F
O
E
解:当F是AE中点时,满足题意
理由如下
连接OF,
∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,
1. 两个全等的正方形ABCD、ABEF不在同
一平面内,M、N是对角线AC、BF的中点
求证:MN ∥面BCE
分析:有两个中点一般考虑中位线
由M、N是中点知:
MN ∥ CE
课堂巩固
连接AE,CE
所以 MN ∥面BCE
证明:连接AE、CE,
∵点N为正方形ABEF对角线BF的中点
∴AE经过点N
又 点M为正方形ABCD 对角线AC的中点
∴ MN//CE
又
2.一木块儿如图所示,点P在平面VAC内,现在准备过点P把木块锯开,且截面与VB、AC平行,请问木工师傅该如何画出该截面与木块儿表面交线?
●
V
P
C
A
B
●
V
P
C
A
B
分析:本题是一道实际问题。要解决问题我们必须要建立必要的数学模型,而这个模型就是直线与平面平行的判定定理。
E
G
H
F
因为点P在表面,因此在表面要找到与VB 、 AC分别平行的线,且这些线在经过点P的同一平面内
●
V
P
C
A
E
G
F
解:在平面ACV 内过点P作直线HE∥AC,交VC、VA于点H、E;然后过点E作VB的平行线交AB于F
∵FE∩EH=E
∴FE、EH确定平面FEH,
H
B
∴AC ∥平面FEH
HE∥AC
反思1:要证明直线与平面平行可以运用判定定理;
反思2:运用定理时一定要注意满足三个条件:
反思3:运用定理的关键是找平行线;找平行线又经常
会用到三角形中位线定理.
“面外、面内、平行”
题后反思总结
1.证明直线与平面平行的方法:
(1)利用定义;
(2)利用判定定理.(关键找到三个条件)
2.数学思想方法:转化的思想
课堂小结
直线与平面没有公共点
两个全等的正方形ABCD、ABEF不在同
一平面内, M、N 是AC,BF上的点且AM=FN。
求证:MN ∥面BCE
课后作业
课本56页T2、63页T1
Q
P
