第五章 位置与坐标单元检测题(含答案)
图片预览

文档简介
位置与坐标单元检测题
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.(2018·南通中考)在平面直角坐标系中点P(1,-2)关于x轴的对称点的坐标是( )
A.(1,2) B.(-1,-2) C.(-1,2) D.(-2,1)
2.如图所示,有一个方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B的位置是( )
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
3.若x轴上的点P到y轴的距离为3,则点P为( )
A.(3,0) B.(3,0)或(-3,0) C.(0,3) D.(0,3)或(0,-3 )
4.若ab>0,则P(a,b)在( )
A.第一象限 B.第一或第三象限 C.第二或第四象限 D.以上都不对
5.点M(m+1,m+3)在x轴上,则M点坐标为( )
A.(0,-4) B.(4,0) C.(-2,0) D.(0,-2)
6.将△ABC的三个顶点的横坐标都加上-1,纵坐标不变,则所得图形与原图形的关系是( )
A.将原图形向x轴的正方向平移了1个单位
B.将原图形向x轴的负方向平移了1个单位
C.将原图形向y轴的正方向平移了1个单位
D.将原图形向y轴的负方向平移了1个单位
7.(2018·邵阳中考)如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1) ,(-3,1),(-1,-1)。30秒后,飞机P飞到P’(4,3)位置,则飞机Q,R的位置Q’,R’分别为( )
A.Q’(2,3),R’(4,1) B.Q’(2,3),R’(2,1) C.Q’(2,2),R’(4,1) D.Q’(3,3),R(3,1)
二、填空题(每小题5分,共25分)
8.已知点P在第二象限,点P到x轴的距离是2,到y轴的距离是3,那么点P的坐标是__________。
9.点P(2x-1,x+3)在第一、三象限的角平分线上,则x的值为_____________。
10.将平面直角坐标系平移,使原点O移至点A(3,-2),这时在新坐标系中原来点O的坐标是________。
11.在平面直角坐标系内,已知点A(2m,m-4)在第四象限,且m为偶数,则m的值为____________。
12.(2017·赤峰中考)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P’(-y+1,x+2),我们把点P’(-y+1,x+2)叫做点P(x,y)的终结点。已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…Pn,…,若点P1的坐标为(2,0),则点P2017的坐标为__________。
三、解答题(共47分)
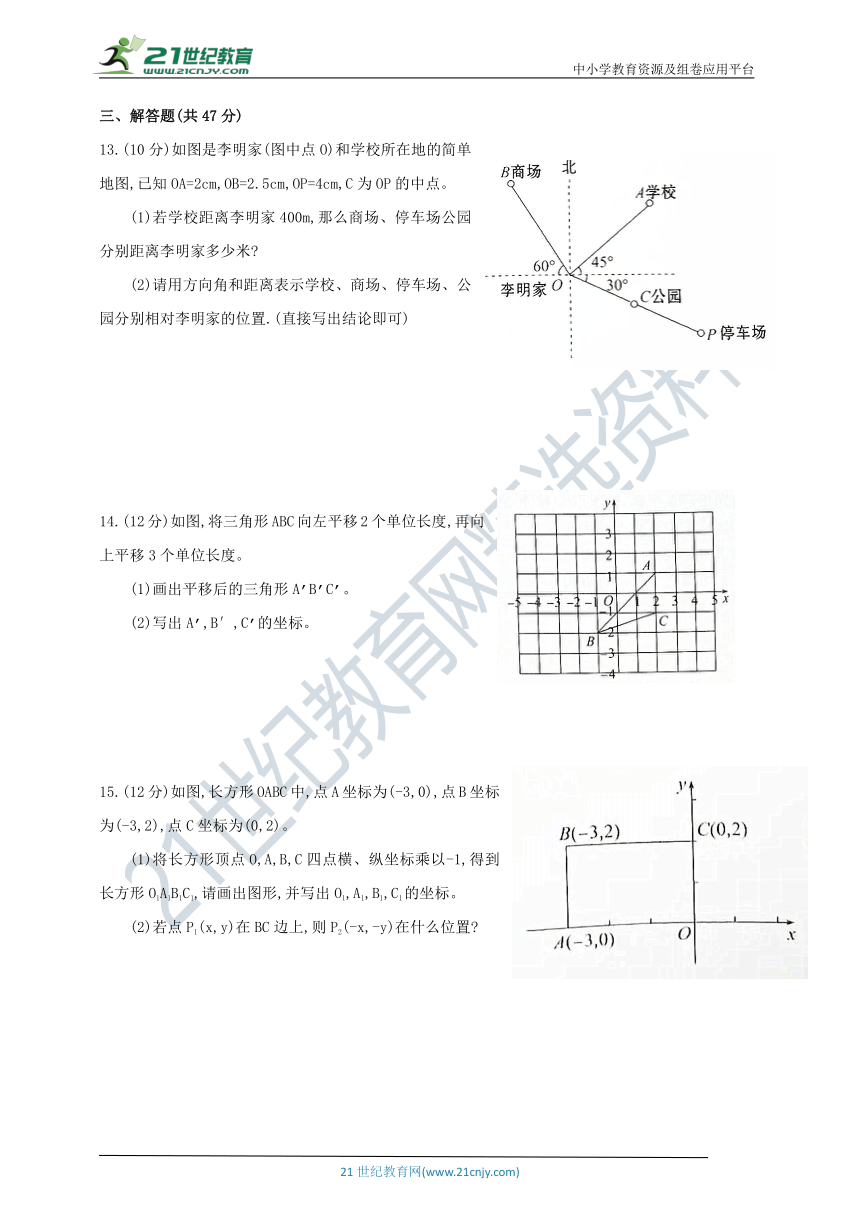
13.(10分)如图是李明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点。
(1)若学校距离李明家400m,那么商场、停车场公园分别距离李明家多少米?
(2)请用方向角和距离表示学校、商场、停车场、公园分别相对李明家的位置.(直接写出结论即可)
14.(12分)如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度。
(1)画出平移后的三角形A’B’C’。
(2)写出A’,B′,C’的坐标。
15.(12分)如图,长方形OABC中,点A坐标为(-3,0),点B坐标为(-3,2),点C坐标为(0,2)。
(1)将长方形顶点O,A,B,C四点横、纵坐标乘以-1,得到长方形O1A1B1C1,请画出图形,并写出O1,A1,B1,C1的坐标。
(2)若点P1(x,y)在BC边上,则P2(-x,-y)在什么位置?
16.(13分)如图,三角形AOB中,A,B两点坐标分别为(2,4),(6,3),求三角形AOB的面积。
参考答案及解析
1.A 2.A 3.B 4.B 5.C 6.B 7.A 8.(-3,2) 9.4 10.(-3,2) 11.2 12.(2,0)
13.解:(1)题图中1cm表示:400÷2=200m,
商场距离李明家:2.5×200=500m,
停车场距离李明家:4×200=800m,
公园距离李明家:4÷2×200=400m
(2)学校位于李明家北偏东45°,离李明家400米;商场位于李明家北偏西30°,离李明家500米;公园位于李明家南偏东60°,离李明家400米;停车场位于李明家南偏东60°,离李明家800米。
14.解:(1)△A’B’C’如图所示.
(2)A’(0,4),B’(-3,1),C’(0,2)。
15.解:(1)如图所示,
O1(0,0),A1(3,0),B1(3,-2),C1(0,-2)
(2)因为点P1(x,y)在BC边上,所以P2(-x,-y)在B1C1上,且与点P1关于原点对称。
16.解:如图,过点A作水平线l交y轴于点E,过点B作垂线,交直线l于点C,交x轴于点D,则
S矩形BCDO=6×4=24,
SRt△AEO=×4×2=4,
SRt△ABC=×1×4=2,
SRt△OBD=×6×3=9,
则S△OAB=S矩形ECDO-SRt△ABC-SRt△AEO-SRt△OBD=9
故三角形AOB的面积是9。
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.(2018·南通中考)在平面直角坐标系中点P(1,-2)关于x轴的对称点的坐标是( )
A.(1,2) B.(-1,-2) C.(-1,2) D.(-2,1)
2.如图所示,有一个方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B的位置是( )
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
3.若x轴上的点P到y轴的距离为3,则点P为( )
A.(3,0) B.(3,0)或(-3,0) C.(0,3) D.(0,3)或(0,-3 )
4.若ab>0,则P(a,b)在( )
A.第一象限 B.第一或第三象限 C.第二或第四象限 D.以上都不对
5.点M(m+1,m+3)在x轴上,则M点坐标为( )
A.(0,-4) B.(4,0) C.(-2,0) D.(0,-2)
6.将△ABC的三个顶点的横坐标都加上-1,纵坐标不变,则所得图形与原图形的关系是( )
A.将原图形向x轴的正方向平移了1个单位
B.将原图形向x轴的负方向平移了1个单位
C.将原图形向y轴的正方向平移了1个单位
D.将原图形向y轴的负方向平移了1个单位
7.(2018·邵阳中考)如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1) ,(-3,1),(-1,-1)。30秒后,飞机P飞到P’(4,3)位置,则飞机Q,R的位置Q’,R’分别为( )
A.Q’(2,3),R’(4,1) B.Q’(2,3),R’(2,1) C.Q’(2,2),R’(4,1) D.Q’(3,3),R(3,1)
二、填空题(每小题5分,共25分)
8.已知点P在第二象限,点P到x轴的距离是2,到y轴的距离是3,那么点P的坐标是__________。
9.点P(2x-1,x+3)在第一、三象限的角平分线上,则x的值为_____________。
10.将平面直角坐标系平移,使原点O移至点A(3,-2),这时在新坐标系中原来点O的坐标是________。
11.在平面直角坐标系内,已知点A(2m,m-4)在第四象限,且m为偶数,则m的值为____________。
12.(2017·赤峰中考)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P’(-y+1,x+2),我们把点P’(-y+1,x+2)叫做点P(x,y)的终结点。已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…Pn,…,若点P1的坐标为(2,0),则点P2017的坐标为__________。
三、解答题(共47分)
13.(10分)如图是李明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点。
(1)若学校距离李明家400m,那么商场、停车场公园分别距离李明家多少米?
(2)请用方向角和距离表示学校、商场、停车场、公园分别相对李明家的位置.(直接写出结论即可)
14.(12分)如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度。
(1)画出平移后的三角形A’B’C’。
(2)写出A’,B′,C’的坐标。
15.(12分)如图,长方形OABC中,点A坐标为(-3,0),点B坐标为(-3,2),点C坐标为(0,2)。
(1)将长方形顶点O,A,B,C四点横、纵坐标乘以-1,得到长方形O1A1B1C1,请画出图形,并写出O1,A1,B1,C1的坐标。
(2)若点P1(x,y)在BC边上,则P2(-x,-y)在什么位置?
16.(13分)如图,三角形AOB中,A,B两点坐标分别为(2,4),(6,3),求三角形AOB的面积。
参考答案及解析
1.A 2.A 3.B 4.B 5.C 6.B 7.A 8.(-3,2) 9.4 10.(-3,2) 11.2 12.(2,0)
13.解:(1)题图中1cm表示:400÷2=200m,
商场距离李明家:2.5×200=500m,
停车场距离李明家:4×200=800m,
公园距离李明家:4÷2×200=400m
(2)学校位于李明家北偏东45°,离李明家400米;商场位于李明家北偏西30°,离李明家500米;公园位于李明家南偏东60°,离李明家400米;停车场位于李明家南偏东60°,离李明家800米。
14.解:(1)△A’B’C’如图所示.
(2)A’(0,4),B’(-3,1),C’(0,2)。
15.解:(1)如图所示,
O1(0,0),A1(3,0),B1(3,-2),C1(0,-2)
(2)因为点P1(x,y)在BC边上,所以P2(-x,-y)在B1C1上,且与点P1关于原点对称。
16.解:如图,过点A作水平线l交y轴于点E,过点B作垂线,交直线l于点C,交x轴于点D,则
S矩形BCDO=6×4=24,
SRt△AEO=×4×2=4,
SRt△ABC=×1×4=2,
SRt△OBD=×6×3=9,
则S△OAB=S矩形ECDO-SRt△ABC-SRt△AEO-SRt△OBD=9
故三角形AOB的面积是9。
