苏科版数学八年级上第5章《平面直角坐标系》综合测试卷(有答案)
文档属性
| 名称 | 苏科版数学八年级上第5章《平面直角坐标系》综合测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-30 08:10:58 | ||
图片预览


文档简介
第5章《平面直角坐标系》综合测试卷
考试时间:90分钟 满分:100分
一、选择(每题3分,共24分)
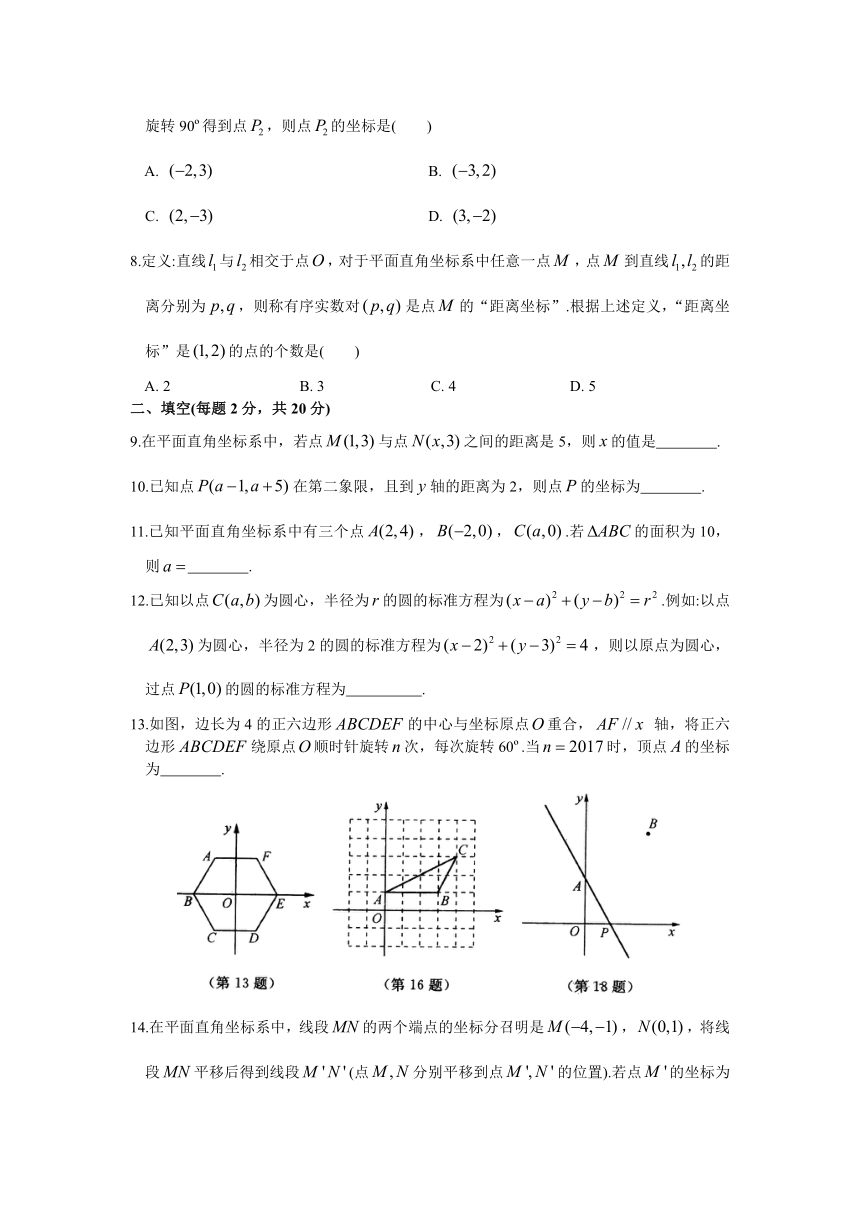
1.一只小虫从点出发,先向右跳4个单位长度,再向下跳3个单位长度,到达点 处,则点的坐标是( )
A. B. C. D.
2.如桌点在轴上,那么点的坐标为( )
A. B. C. D.
3. 在平面直角坐标系中,若点与点关于轴对称,点的坐标是,则点的坐标是( )
A. B. C. D.
4. 如图,在平面直角坐标系中,位于第二象限,点的坐标是,先把向右平移4个单位长度得到,再作与关于轴对称的,则点的对应点的坐标是( )
A. B. C. D.
5.若点在轴下方,轴左侧,且,,则点的坐标为( )
A. B. C. D.
6.如图,动点从出发,沿如图所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点第2 018次碰到长方形的边时,点的坐标为( )
A.(1,4) B. (5,0) C. (7,4) D. (8,3)
7. 在平面直角坐标系中,点向右平移7个单位长度得到点,点绕原点逆时针旋转90o得到点,则点的坐标是( )
A. B.
C. D.
8.定义:直线与相交于点,对于平面直角坐标系中任意一点,点到直线的距离分别为,则称有序实数对是点的“距离坐标”.根据上述定义,“距离坐标”是的点的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空(每题2分,共20分)
9.在平面直角坐标系中,若点与点之间的距离是5,则的值是 .
10.已知点在第二象限,且到轴的距离为2,则点的坐标为 .
11.已知平面直角坐标系中有三个点,,.若的面积为10,则 .
12.已知以点为圆心,半径为的圆的标准方程为.例如:以点为圆心,半径为2的圆的标准方程为,则以原点为圆心,过点的圆的标准方程为 .
13.如图,边长为4的正六边形的中心与坐标原点重合, 轴,将正六边形绕原点顺时针旋转次,每次旋转60o.当时,顶点的坐标为 .
14.在平面直角坐标系中,线段的两个端点的坐标分召明是,,将线段平移后得到线段(点分别平移到点的位置).若点的坐标为,则点的坐标为 .
15.已知正方形在平面直角坐标系中,,,那么点的坐标为 ,点的坐标为 .
16.如图,在中,点的坐标为,点的坐标为.如果要使与 全等,那么点的坐标是 .
17.在平面直角坐标系中有三个点,,,点 关于点的对称点为;点关于点的对称点力,点关于点的对称点为,按此规律继续以点为对枷中心重复前面的操作,依次得到点,...,则点的坐标是 .
18.如图,点的坐标分别为,,点为轴上的一个动点.若点关于直线的对称点恰好落在坐标轴上,则点的坐标为 .
三、解答(共56分)
19. ( 6分)如图,在平面直角坐标系中,小正方形网格的边长为1个单位长度,的三个顶点的坐标分别为,,.
(1)画出关于轴对称的;
(2)画出将绕原点按逆时针方向旋转90o得到的.
20. ( 6分)如图,,,.
(1)求点到轴的距离;
(2)求的三边长;
(3)当点在轴上,且的面积为6时,请直接写出点的坐标.
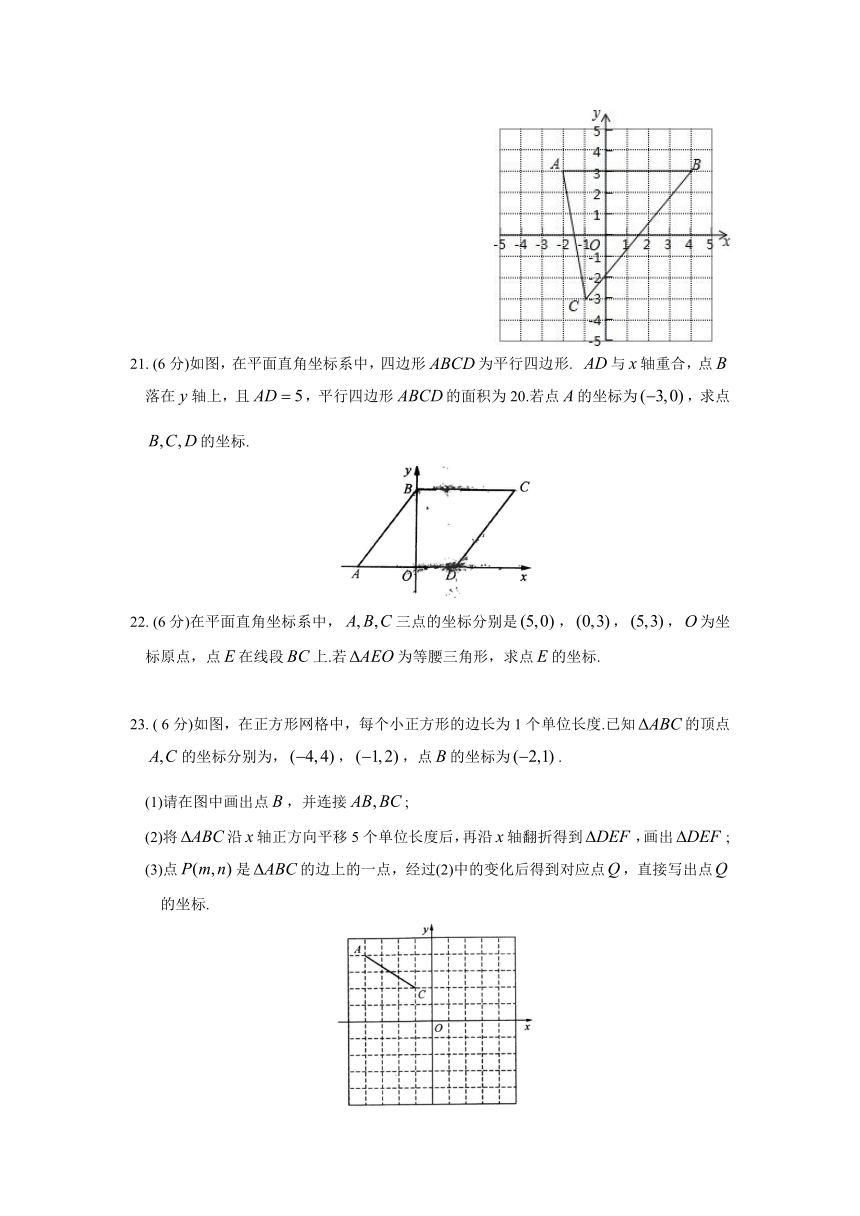
21. (6分)如图,在平面直角坐标系中,四边形为平行四边形. 与轴重合,点 落在轴上,且,平行四边形的面积为20.若点的坐标为,求点的坐标.
22. (6分)在平面直角坐标系中,三点的坐标分别是,,,为坐标原点,点在线段上.若为等腰三角形,求点的坐标.
23. ( 6分)如图,在正方形网格中,每个小正方形的边长为1个单位长度.已知的顶点的坐标分别为,,,点的坐标为.
(1)请在图中画出点,并连接;
(2)将沿轴正方向平移5个单位长度后,再沿轴翻折得到,画出;
(3)点是的边上的一点,经过(2)中的变化后得到对应点,直接写出点 的坐标.
24. ( 8分)如图,在平面直角坐标系中,,,以线段为直角边在第一象限内作等腰直角三角形,.点是轴上的一个动点,设.
(1)求的面积;
(2)若是等腰三角形,求点的坐标;
(3)是否存在这样的点,使得的值最大?如果不存在,请说明理由;如果存在,请在图中标出点的位置.
25. (8分)如图,在平面直角坐标系中(以1 cm为1个单位长度),过点的直线垂直于轴,点为直线上一点,点从点出发,以2 cm/s的速度沿直线向左移动;同时,点从原点出发,以1 cm/s的速度沿轴向右移动.
(1)求几秒后平行于轴;
(2)若以为顶点的四边形的面积是10 cm2,求点的坐标.
26. (10分)数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数间题中的应用.
探究一:求不等式的解集
(1)探究的几何意义.
如图①,在以点为原点的数轴上,设点对应的数是,由绝对值的定义可知,点与点的距离为,可记为.将线段向右平移1个单位长度得到线段,此时点对应的数是,点对应的数是1.因为,所以.因此,的几何意义可以理解为数轴上所对应的点与1所对应的点之间的距离 .
(2)求方程的解.
因为数轴上3和所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,.
(3)求不等式的解集.
因为表示数轴上所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数的范围.
请在图②的数轴上表示的解集,并写出这个解集.
探究二:探究了的几何意义
(1)探究的几何意义.
如图③,在平面直角坐标系中,设点的坐标为,过点作轴于点,作轴于点,则点的坐标为,点的坐标为,即,.在中,,则 .因此,的几何意义可以理解为点与点之间的距离.
(2)探究的几何意义.
如图④,在平面直角坐标系中,设点的坐标为,由探究二(1)可知,,将线段先向右平移1个单位长度,再向上平移5个单位长度,得到线段,此时点的坐标为,点的坐标为.因为,所以,因此的几何意义可以理解为点与点之间的距离.
(3)探究的几何意义.
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为 .
拓展应用
(1) 的几何意义可以理解为点与点之间的距离和点与点 (填写坐标)之间的距离之和;
(2)的最小值为 (直接写出结果).
参考答案
1-8 BBABACAC
9. ―4或6
10. (―2,4)
11. 3或―7
12.
13.
14. (2,4)
15. (4,0)或(4,4) (2,0)或(2,4)
16. (4,―1)或(―1,―1)或(―1,3)
17. (2,―4)
18. (―4, 0)或(0,―2)或(0,8)
19. (1) 如图,即为所求;
(2) 如图,即为所求
20.(1)距离为3
(2)
(3)
21.
22.
23.(1)如图所示
(2)如图所示
(3)
24.(1)面积为12.5
(2)点的坐标为或或或
(3) 存在点,点位置如下图
25.(1)3s
(2)点的坐标为或
26.探究一
(3)如图,解集为
探究二
(3)图略
(4)在平面直角坐标系中,点与点之间的距离
拓展应用
(1)(―1,―5) (2)5
考试时间:90分钟 满分:100分
一、选择(每题3分,共24分)
1.一只小虫从点出发,先向右跳4个单位长度,再向下跳3个单位长度,到达点 处,则点的坐标是( )
A. B. C. D.
2.如桌点在轴上,那么点的坐标为( )
A. B. C. D.
3. 在平面直角坐标系中,若点与点关于轴对称,点的坐标是,则点的坐标是( )
A. B. C. D.
4. 如图,在平面直角坐标系中,位于第二象限,点的坐标是,先把向右平移4个单位长度得到,再作与关于轴对称的,则点的对应点的坐标是( )
A. B. C. D.
5.若点在轴下方,轴左侧,且,,则点的坐标为( )
A. B. C. D.
6.如图,动点从出发,沿如图所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点第2 018次碰到长方形的边时,点的坐标为( )
A.(1,4) B. (5,0) C. (7,4) D. (8,3)
7. 在平面直角坐标系中,点向右平移7个单位长度得到点,点绕原点逆时针旋转90o得到点,则点的坐标是( )
A. B.
C. D.
8.定义:直线与相交于点,对于平面直角坐标系中任意一点,点到直线的距离分别为,则称有序实数对是点的“距离坐标”.根据上述定义,“距离坐标”是的点的个数是( )
A. 2 B. 3 C. 4 D. 5
二、填空(每题2分,共20分)
9.在平面直角坐标系中,若点与点之间的距离是5,则的值是 .
10.已知点在第二象限,且到轴的距离为2,则点的坐标为 .
11.已知平面直角坐标系中有三个点,,.若的面积为10,则 .
12.已知以点为圆心,半径为的圆的标准方程为.例如:以点为圆心,半径为2的圆的标准方程为,则以原点为圆心,过点的圆的标准方程为 .
13.如图,边长为4的正六边形的中心与坐标原点重合, 轴,将正六边形绕原点顺时针旋转次,每次旋转60o.当时,顶点的坐标为 .
14.在平面直角坐标系中,线段的两个端点的坐标分召明是,,将线段平移后得到线段(点分别平移到点的位置).若点的坐标为,则点的坐标为 .
15.已知正方形在平面直角坐标系中,,,那么点的坐标为 ,点的坐标为 .
16.如图,在中,点的坐标为,点的坐标为.如果要使与 全等,那么点的坐标是 .
17.在平面直角坐标系中有三个点,,,点 关于点的对称点为;点关于点的对称点力,点关于点的对称点为,按此规律继续以点为对枷中心重复前面的操作,依次得到点,...,则点的坐标是 .
18.如图,点的坐标分别为,,点为轴上的一个动点.若点关于直线的对称点恰好落在坐标轴上,则点的坐标为 .
三、解答(共56分)
19. ( 6分)如图,在平面直角坐标系中,小正方形网格的边长为1个单位长度,的三个顶点的坐标分别为,,.
(1)画出关于轴对称的;
(2)画出将绕原点按逆时针方向旋转90o得到的.
20. ( 6分)如图,,,.
(1)求点到轴的距离;
(2)求的三边长;
(3)当点在轴上,且的面积为6时,请直接写出点的坐标.
21. (6分)如图,在平面直角坐标系中,四边形为平行四边形. 与轴重合,点 落在轴上,且,平行四边形的面积为20.若点的坐标为,求点的坐标.
22. (6分)在平面直角坐标系中,三点的坐标分别是,,,为坐标原点,点在线段上.若为等腰三角形,求点的坐标.
23. ( 6分)如图,在正方形网格中,每个小正方形的边长为1个单位长度.已知的顶点的坐标分别为,,,点的坐标为.
(1)请在图中画出点,并连接;
(2)将沿轴正方向平移5个单位长度后,再沿轴翻折得到,画出;
(3)点是的边上的一点,经过(2)中的变化后得到对应点,直接写出点 的坐标.
24. ( 8分)如图,在平面直角坐标系中,,,以线段为直角边在第一象限内作等腰直角三角形,.点是轴上的一个动点,设.
(1)求的面积;
(2)若是等腰三角形,求点的坐标;
(3)是否存在这样的点,使得的值最大?如果不存在,请说明理由;如果存在,请在图中标出点的位置.
25. (8分)如图,在平面直角坐标系中(以1 cm为1个单位长度),过点的直线垂直于轴,点为直线上一点,点从点出发,以2 cm/s的速度沿直线向左移动;同时,点从原点出发,以1 cm/s的速度沿轴向右移动.
(1)求几秒后平行于轴;
(2)若以为顶点的四边形的面积是10 cm2,求点的坐标.
26. (10分)数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数间题中的应用.
探究一:求不等式的解集
(1)探究的几何意义.
如图①,在以点为原点的数轴上,设点对应的数是,由绝对值的定义可知,点与点的距离为,可记为.将线段向右平移1个单位长度得到线段,此时点对应的数是,点对应的数是1.因为,所以.因此,的几何意义可以理解为数轴上所对应的点与1所对应的点之间的距离 .
(2)求方程的解.
因为数轴上3和所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,.
(3)求不等式的解集.
因为表示数轴上所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数的范围.
请在图②的数轴上表示的解集,并写出这个解集.
探究二:探究了的几何意义
(1)探究的几何意义.
如图③,在平面直角坐标系中,设点的坐标为,过点作轴于点,作轴于点,则点的坐标为,点的坐标为,即,.在中,,则 .因此,的几何意义可以理解为点与点之间的距离.
(2)探究的几何意义.
如图④,在平面直角坐标系中,设点的坐标为,由探究二(1)可知,,将线段先向右平移1个单位长度,再向上平移5个单位长度,得到线段,此时点的坐标为,点的坐标为.因为,所以,因此的几何意义可以理解为点与点之间的距离.
(3)探究的几何意义.
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为 .
拓展应用
(1) 的几何意义可以理解为点与点之间的距离和点与点 (填写坐标)之间的距离之和;
(2)的最小值为 (直接写出结果).
参考答案
1-8 BBABACAC
9. ―4或6
10. (―2,4)
11. 3或―7
12.
13.
14. (2,4)
15. (4,0)或(4,4) (2,0)或(2,4)
16. (4,―1)或(―1,―1)或(―1,3)
17. (2,―4)
18. (―4, 0)或(0,―2)或(0,8)
19. (1) 如图,即为所求;
(2) 如图,即为所求
20.(1)距离为3
(2)
(3)
21.
22.
23.(1)如图所示
(2)如图所示
(3)
24.(1)面积为12.5
(2)点的坐标为或或或
(3) 存在点,点位置如下图
25.(1)3s
(2)点的坐标为或
26.探究一
(3)如图,解集为
探究二
(3)图略
(4)在平面直角坐标系中,点与点之间的距离
拓展应用
(1)(―1,―5) (2)5
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
