沪科版八年级数学上册15.4.2角的平分线的性质课件(共27张PPT)
文档属性
| 名称 | 沪科版八年级数学上册15.4.2角的平分线的性质课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 378.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-02 21:59:12 | ||
图片预览






文档简介
15.4.2角平分线的性质
沪科版八年级数学上册
旧知回顾
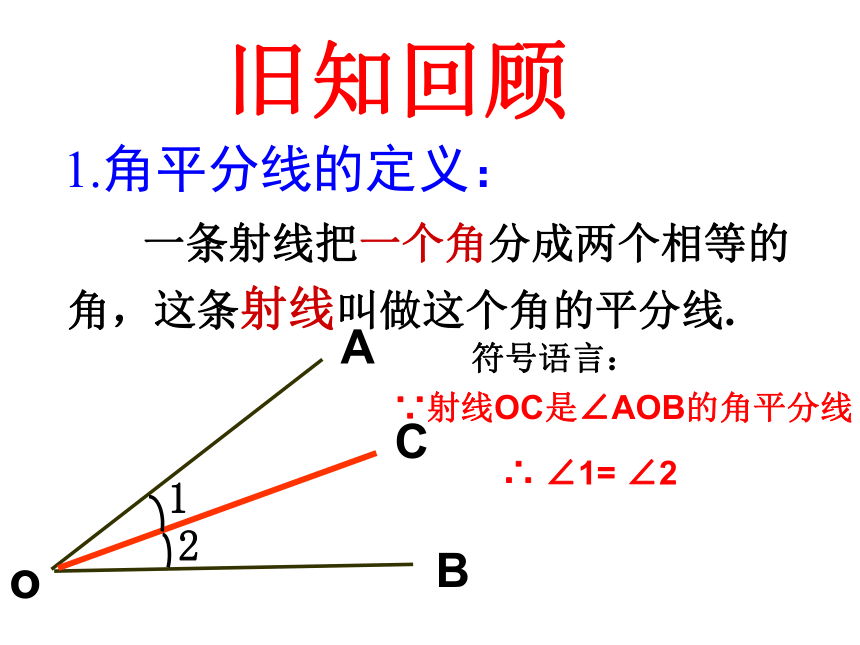
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
o
B
C
A
1
2
符号语言:
∵射线OC是∠AOB的角平分线
∴ ∠1= ∠2
1.角平分线的定义:
2、点到直线距离:
从直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离.
O
P
A
B
点P到直线AB的距离就是垂线段PO的长度
旧知回顾
旧知回顾
3.三角形的角平分线:
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
如何做角平分线呢?
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
情境问题
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
活动2
A
D
B
C
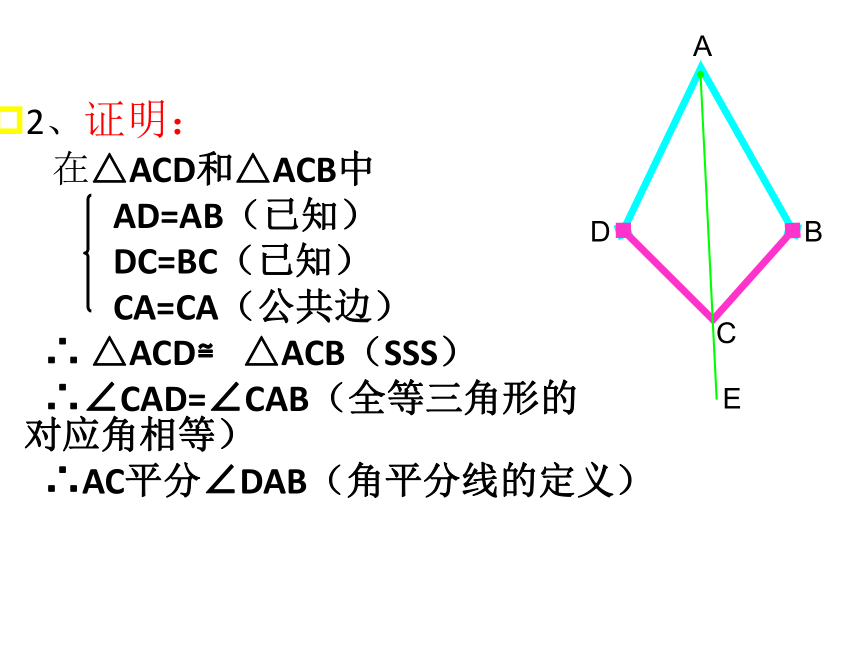
2、证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
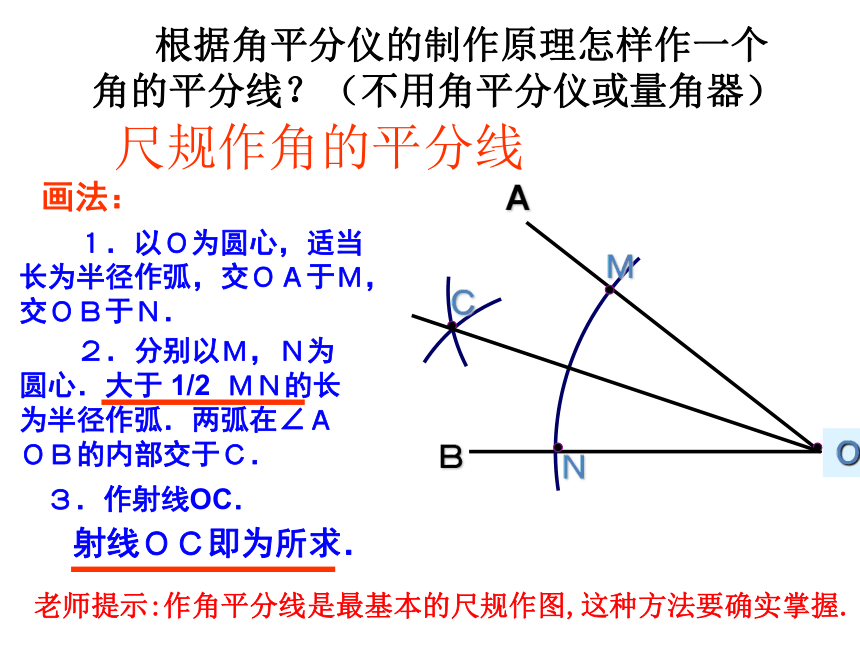
尺规作角的平分线
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
老师提示:作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
M
N
C
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC
求证:OC平分∠AOB
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
实践应用
角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,
写出结论:____________
PD PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
www.12999.com
角平分线的性质:角的平分线上的点 到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
猜想:
C
数学符号表示已知和求证:
即
注意
特别是文字性叙述的几何证明题
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
你还可以得到其他什么结论?
1.先证所缺条件
2.写齐条件:一个中心三个基本点
1.OD=OE
2.PO是∠DPE的平分线
O
D
E
P
P到OA的距离
P到OB的距离
角平分线上的点
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB
∴ PD= PE
A
C
B
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
不必再证全等
作用:
判断线段相等的依据.
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
判断正误:
练习1
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
随课巩固
例1:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为?
A
C
D
B
E
E
DE=CD=BC-BD=8-5=3
在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D.
求证:AC=BD.
O
A
B
E
C
D
课堂练习
提示:有角平分线的条件,常考虑角平分线性质
要证∴ △AEC≌△BED
有哪些条件?需要先证吗?
请写出证明过程
例2:如图,△ABC的角平分线BM、CN相交于点P。求证:点P到三角形三边的距离均相等。
A
B
C
P
E
D
F
M
N
例题讲解
N
D
N
A
B
C
P
D
N
A
B
C
P
D
N
E
F
A
B
C
P
D
N
A
B
C
P
A
B
C
P
点拨:有角平分线时,常过角平分线上的点向角的两边作垂线段
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BF是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
A
B
C
P
D
E
F
结论:两内角平分线的交点到三边的距离相等
练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
A
B
C
D
E
P
F
G
H
B
P
证明:过点P作PG 、PF、PH分别垂直于AB、BC、CA,垂足为G、F、H
∵BD是△ABC的角平分线,点P在BM上
∴PG=PF
(在角平分线上的点到角的两边的距离相等)
同理 PF=PH.
∴ PG=PF=PH.
即点P到边AB、BC、 CA的距离相等
两外角平分线的交点到三边的距离相等
①
②
③
得到结论:
小结:
及画一条已知直线的垂线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
判断线段相等的依据.
1.如何作一个已知角的角平分线
沪科版八年级数学上册
旧知回顾
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
o
B
C
A
1
2
符号语言:
∵射线OC是∠AOB的角平分线
∴ ∠1= ∠2
1.角平分线的定义:
2、点到直线距离:
从直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离.
O
P
A
B
点P到直线AB的距离就是垂线段PO的长度
旧知回顾
旧知回顾
3.三角形的角平分线:
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
如何做角平分线呢?
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
情境问题
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
活动2
A
D
B
C
2、证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
尺规作角的平分线
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
老师提示:作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
M
N
C
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC
求证:OC平分∠AOB
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
实践应用
角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,
写出结论:____________
PD PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
www.12999.com
角平分线的性质:角的平分线上的点 到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
猜想:
C
数学符号表示已知和求证:
即
注意
特别是文字性叙述的几何证明题
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
你还可以得到其他什么结论?
1.先证所缺条件
2.写齐条件:一个中心三个基本点
1.OD=OE
2.PO是∠DPE的平分线
O
D
E
P
P到OA的距离
P到OB的距离
角平分线上的点
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB
∴ PD= PE
A
C
B
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
不必再证全等
作用:
判断线段相等的依据.
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
判断正误:
练习1
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
4
随课巩固
例1:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为?
A
C
D
B
E
E
DE=CD=BC-BD=8-5=3
在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D.
求证:AC=BD.
O
A
B
E
C
D
课堂练习
提示:有角平分线的条件,常考虑角平分线性质
要证∴ △AEC≌△BED
有哪些条件?需要先证吗?
请写出证明过程
例2:如图,△ABC的角平分线BM、CN相交于点P。求证:点P到三角形三边的距离均相等。
A
B
C
P
E
D
F
M
N
例题讲解
N
D
N
A
B
C
P
D
N
A
B
C
P
D
N
E
F
A
B
C
P
D
N
A
B
C
P
A
B
C
P
点拨:有角平分线时,常过角平分线上的点向角的两边作垂线段
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BF是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
A
B
C
P
D
E
F
结论:两内角平分线的交点到三边的距离相等
练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
A
B
C
D
E
P
F
G
H
B
P
证明:过点P作PG 、PF、PH分别垂直于AB、BC、CA,垂足为G、F、H
∵BD是△ABC的角平分线,点P在BM上
∴PG=PF
(在角平分线上的点到角的两边的距离相等)
同理 PF=PH.
∴ PG=PF=PH.
即点P到边AB、BC、 CA的距离相等
两外角平分线的交点到三边的距离相等
①
②
③
得到结论:
小结:
及画一条已知直线的垂线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
判断线段相等的依据.
1.如何作一个已知角的角平分线
