15.4.2角平分线的性质课件课件(共27张PPT)
文档属性
| 名称 | 15.4.2角平分线的性质课件课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 684.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-02 22:05:17 | ||
图片预览








文档简介
15.4.2角平分线的性质
★ 什么是角的平分线?怎样画一个角的平分线?
操作与思考1:
B
O
A
C
信不信由你
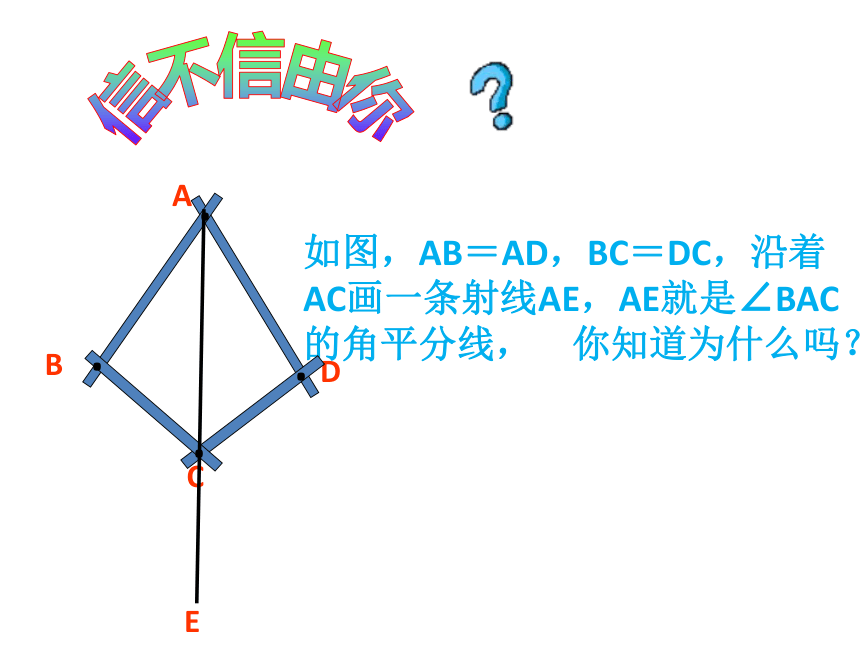
如图,AB=AD,BC=DC,沿着AC画一条射线AE,AE就是∠BAC的角平分线, 你知道为什么吗?
D
·
·
·
·
C
B
A
E
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
如何用尺规作角的平分线?
A
B
O
M
N
C
作法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
3.作射线OC.
则射线OC即为所求.
探究
探索1
将角AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?
O
A
B
A
O
B
E
D
角平分线上的点到角的两边的距离相等。
在∠AOB的平分线OC上任取一点P,然后,作点P到∠AOB两边的垂线段PD、PE,画一画,量一量,从中你有什么新发现?你能说明其中的道理吗?
B
O
A
C
·
D
P
E
画一画,想一想,议一议
命题:在角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
角平分线的性质
定理:在角平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE.
随堂练习
B
O
A
C
·
D
P
E
1.如图,OC是∠AOB的平分线, ∵
∴PD=PE
PD⊥OA,PE⊥OB
2.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且CD:DB=1:2,则点D到AB的距离为_________。
动脑筋
3.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6, 求BE,AE的长和△AED的周长。
E
D
C
B
A
练一练
3在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。
E
D
C
B
A
4.△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
(点D到AB的距离是3)
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
议一议
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
解:设要截取的长度为Xm,则:
要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)
S
O
公路
铁路
解得:X=0.025m
=2.5cm
A
则点A即为所求的点
想一想
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
作射线OP
\ 点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
角平分线的判定
B
A
D
O
P
E
∵
角平分线的判定的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
角平分线的性质:在角的平分线上的点到这个角的两边的距离相等。
角平分线的判定到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
例1.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,
且BE=CF。求证:AD是△ABC的角平分线。
A
B
C
E
F
D
4.已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)
B
C
A
C′
5已知:如图,BE⊥AC于E, CF⊥AB于F,BE、CF相交于D, BD=CD 。
求证: AD平分∠BAC 。
A
B
C
F
E
D
课堂练习
例 已知:如图,△ABC的角平分线BM、CN相 交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上(已知)
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
练习:
如图,三条公路相交,现在要修建一加油站,使加油站到三条公路的距离相等,问加油站该选在什么位置上?
拓展与延伸
1、已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
2、已知PA=PB, ∠1+ ∠2=1800,
求证:OP平分∠AOB
A
O
B
P
1
2
E
F
3 已知:如图,△ABC的∠B的外角的平分线BD和∠C的外角平分线CE相交于点P。
求证:点P在∠BAC的平分线上。
C
A
B
P
D
E
课堂小结
1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.
★ 什么是角的平分线?怎样画一个角的平分线?
操作与思考1:
B
O
A
C
信不信由你
如图,AB=AD,BC=DC,沿着AC画一条射线AE,AE就是∠BAC的角平分线, 你知道为什么吗?
D
·
·
·
·
C
B
A
E
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
如何用尺规作角的平分线?
A
B
O
M
N
C
作法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
3.作射线OC.
则射线OC即为所求.
探究
探索1
将角AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?
O
A
B
A
O
B
E
D
角平分线上的点到角的两边的距离相等。
在∠AOB的平分线OC上任取一点P,然后,作点P到∠AOB两边的垂线段PD、PE,画一画,量一量,从中你有什么新发现?你能说明其中的道理吗?
B
O
A
C
·
D
P
E
画一画,想一想,议一议
命题:在角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
角平分线的性质
定理:在角平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE.
随堂练习
B
O
A
C
·
D
P
E
1.如图,OC是∠AOB的平分线, ∵
∴PD=PE
PD⊥OA,PE⊥OB
2.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且CD:DB=1:2,则点D到AB的距离为_________。
动脑筋
3.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6, 求BE,AE的长和△AED的周长。
E
D
C
B
A
练一练
3在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。
E
D
C
B
A
4.△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
(点D到AB的距离是3)
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
议一议
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
解:设要截取的长度为Xm,则:
要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)
S
O
公路
铁路
解得:X=0.025m
=2.5cm
A
则点A即为所求的点
想一想
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
作射线OP
\ 点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
角平分线的判定
B
A
D
O
P
E
∵
角平分线的判定的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
角平分线的性质:在角的平分线上的点到这个角的两边的距离相等。
角平分线的判定到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
例1.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,
且BE=CF。求证:AD是△ABC的角平分线。
A
B
C
E
F
D
4.已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)
B
C
A
C′
5已知:如图,BE⊥AC于E, CF⊥AB于F,BE、CF相交于D, BD=CD 。
求证: AD平分∠BAC 。
A
B
C
F
E
D
课堂练习
例 已知:如图,△ABC的角平分线BM、CN相 交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上(已知)
∴PD=PE(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
练习:
如图,三条公路相交,现在要修建一加油站,使加油站到三条公路的距离相等,问加油站该选在什么位置上?
拓展与延伸
1、已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.
A
A
A
A
A
A
A
D
N
E
B
F
M
C
A
2、已知PA=PB, ∠1+ ∠2=1800,
求证:OP平分∠AOB
A
O
B
P
1
2
E
F
3 已知:如图,△ABC的∠B的外角的平分线BD和∠C的外角平分线CE相交于点P。
求证:点P在∠BAC的平分线上。
C
A
B
P
D
E
课堂小结
1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.
