4.1.1 立体图形与平面图形课时作业(1)
文档属性
| 名称 | 4.1.1 立体图形与平面图形课时作业(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-30 19:03:10 | ||
图片预览



文档简介
4.1.1 立体图形与平面图形课时作业(1)
姓名:__________班级:__________考号:__________
一 、选择题
1.在如图所示可爱的小猫图案中,没有用到的图形是
A. 长方形 B. 三角形 C. 八边形 D. 五边形
2.下列各组图形都是平面图形的一组是( )
A. 线段、圆、圆锥、球 B. 角、三角形、长方形、圆柱
C. 长方体、圆柱、棱锥、球 D. 角、三角形、正方形、圆
3.判断下列语句错误的是( )
A. 棱柱、球是立体图形,角、直线、三角形、圆是平面图形
B. 两点的所有连线中,线段最短
C. 经过平面上任意两点有且只有两条直线
D. 把一条射线绕着它的端点旋转而形成的图形叫做角
4.以下几种图形:
①三角形;②正方体;③圆;④圆锥;⑤圆柱;⑥正方形;⑦梯形;⑧球;⑨等腰三角形;
其中不属于平面图形的是( )
A. ②③④⑧ B. ②④⑤ C. ④⑤⑧⑨ D. ②④⑤⑧
5.如图所示的几何体的面数是( )
A. 3 B. 4 C. 5 D. 6
6.在八面体顶点数V、面数F、棱数E中,V+F-E=( )
A. 16 B. 6 C. 4 D. 2
二 、填空题
7.六棱柱是一个立体图形,它是由_____个面,_____条棱,_____个顶点组成的.
8.一个正六棱柱模型,它的上、下底面的形状、大小都相同,底面边长都是,侧棱长,则它的所有侧面的面积之和为________.
9.在下图所示立体图形中,(1)球体有____;(2)柱体有____;(3)锥体有____.
10.若正方体棱长的和是36,则它的体积是____.
11.一个正方体的表面涂满了同种颜色,按如图所示将它切成个大小相等的小立方块.设其中仅有个面涂有颜色的小立方块的个数为,则、、之间的数量关系为________.
三 、解答题
12.请给以下各图分类.
13.如图,左面的几何体叫三棱柱,它有五个面,条棱,个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
四棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
14.小明爱好手工制作,星期天小明纸板制作了一个正五棱柱的笔筒,它的底面边长是5厘米,侧棱长是6厘米,回答下列问题:
(1)这个笔筒一共有多少个面?多少条棱?
(2)制作侧面共用去多少材料?
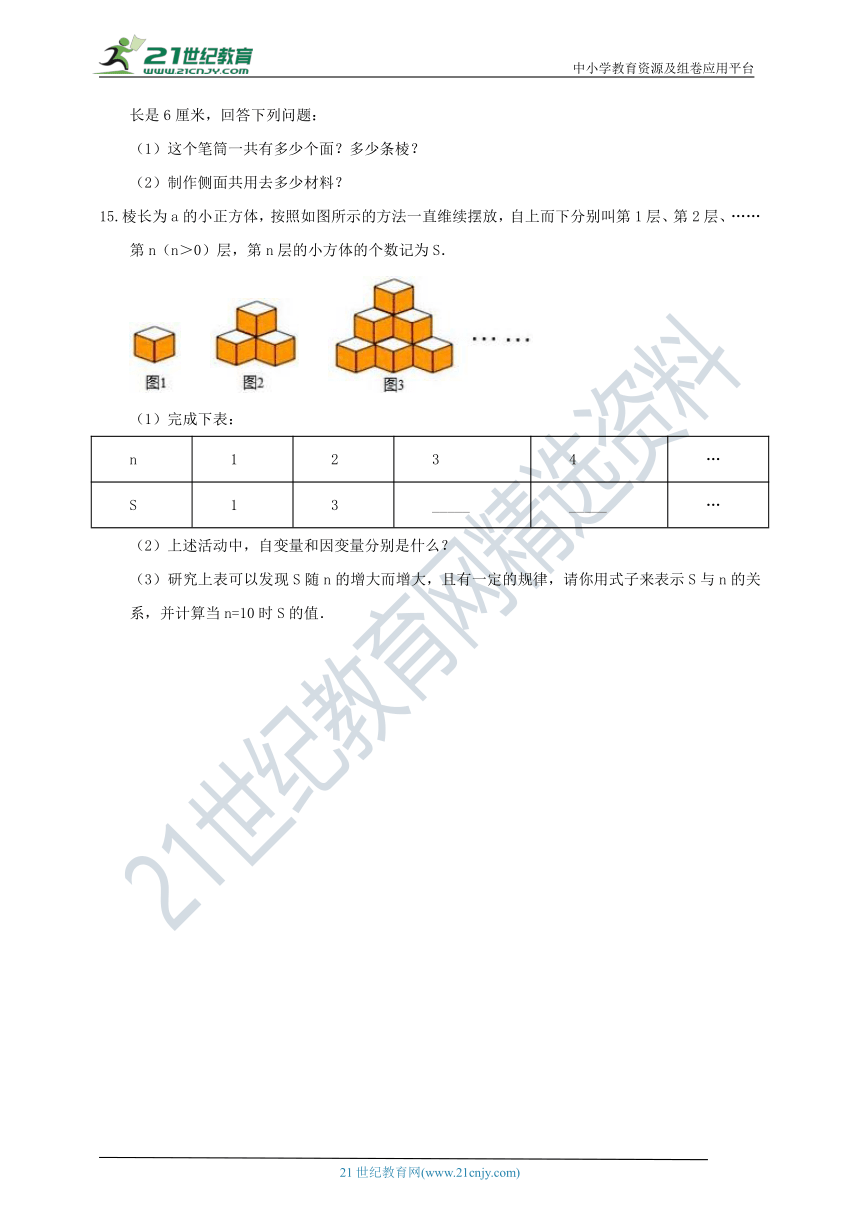
15.棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.
(1)完成下表:
n
1
2
3
4
…
S
1
3
_____
_____
…
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.
答案解析
一 、选择题
1.【考点】认识立体图形
【分析】观察图形即可解答.
解:由图可知,构成小猫图案的图形有:三角形、圆、长方形,五边形和六边形.
∴在上述四个选项所涉及的图形中,只有八边形在小猫图案中没有用到.
故选C.
【点睛】本题考查了图形的识别,仔细观察图形是解决本题的关键.
2.【考点】平面图形
【分析】根据平面图形定义:一个图形的各部分都在同一个平面内的图形是平面图形可得答案.
解:A、线段、圆、圆锥、球中,圆锥、球不是平面图形,故此选项错误;
B、角、三角形、长方形、圆柱中,圆柱不是平面图形,故此选项错误;
C、长方体、圆柱、棱锥、球中都不是平面图形,故此选项错误;
D、角、三角形、正方形、圆都是平面图形,故此选项正确;
所以D选项是正确的.
【点睛】此题主要考查了平面图形,关键是掌握平面图形的定义.
3.【考点】认识立体图形
【分析】根据立体图形的认识,线段的性质,直线的性质,角的概念即可作出选择.
解:A、棱柱、球是立体图形,角、直线、三角形、圆是平面图形是正确的,不符合题意;
B、两点的所有连线中,线段最短是正确的,不符合题意;
C、经过平面上任意两点有且只有一条直线,原来的说法是错误的,符合题意;
D、把一条射线绕着它的端点旋转而形成的图形叫做角是正确的,不符合题意.
故选:C.
【点睛】考查了立体图形的认识,线段的性质,直线的性质,角的概念,是基础题型,关键是熟练掌握相关的知识.
4.【考点】平面图形
【分析】平面图形定义:一个图形的各部分都在同一个平面内,如:线段、 角、 三角形、 正方形、 圆等.
解:1三角形、3圆、6正方形、7梯形、9等腰三角形都是平面图形.
2正方体、4圆锥、5圆柱、8球都是立体图形.
综上所述,不属于平面图形的是:2 4 5 8.
所以D选项是正确的.
【点睛】本题考查立体图形的定义,要注意与平面图形的区分.
5.【考点】认识立体图形
【分析】根据几何的特点,面有底面和侧面.
解:如图所示的几何体的面数是5.
故选:C
【点睛】本题考核知识点:几何体的面. 解题关键点:理解几何体的特点.
6.【考点】认识立体图形
【分析】根据八面体的结构特征进行求解即可得.
解:如图,可知八面体顶点数V=6、面数F=8、棱数E=12,
所以V+F-E=6+8-12=2,
故选D.
【
点睛】本题考查了多面体的顶点数V、面数F、棱数E间的关系,仔细观察图形是解题的关键.
二 、填空题
7.【考点】认识立体图形
【分析】根据六棱柱的概念和定义进行解答即可得.
解:如图,六棱柱上下两个底面是6边形,侧面是6个长方形,
所以共有8个面,18条棱,12个顶点,
故答案为:8,18,12.
【点睛】本题考查了认识立体图形,解决本题的关键是掌握六棱柱的构造特点.
8.【考点】认识立体图形
【分析】对题意进行分析,结合正六棱柱的性质,即可求得答案.
解:正六棱柱的侧面有六个小长方形组成,长方形的长为5cm,宽为4cm,
故侧面面积S=6×5×4=120cm2.
故答案为:120cm2.
【点睛】考查了正六棱柱的侧面展开图和面积的求法,解答此题的关键是掌握六棱柱的展开图.
9.【考点】认识立体图形
【分析】根据球体,柱体,锥体的特点进行分类即可. 空间中到定点的距离等于定长的所有点组成的图形叫做球,球体是一个连续曲面的立体图形,由球面围成的几何体称为球体;柱体:一个多面体有两个面互相平行且大小相同,余下的每个相邻两个面的交线互相平行,这样的多面体称为柱; 圆锥和棱锥这样的立体图形是锥体
解:在下图所示立体图形中,(1)球体有⑦;(2)柱体有①③⑤;(3)锥体有②④⑥.
故答案为:(1). ⑦ (2). ①③⑤ (3). ②④⑥
【点睛】本题考核知识点:认识几何体.解题关键点:认识常见几何体的特点.
10.【考点】认识立体图形
【分析】首先用棱长总和除以12求出棱长,再根据正方体的体积公式,把数据代入公式解答.
解:36÷12=3,
V=a3=3×3×3=27,
它的体积是27.
【点睛】本题考查的是正方体的体积公式,熟练掌握这一点是解题的关键.
11.【考点】认识立体图形
【分析】根据题图分别找出3个面,2个面,1个面涂有颜色的正方体即可.
解:由题图可知:在原正方体的8个顶点处的8个小正方体上,有3个面涂有颜色;2个面涂有颜色的小正方体有12个,1个面涂有颜色的小正方体有6个,
则6﹣12+8=2.
故答案为:.
【点睛】本题主要考查认识立体几何图形,根据已知得出涂有颜色不同的小立方体的个数是解题关键.
三 、解答题
12.【考点】认识立体图形
【分析】主要根据几何体和柱体、椎体、台体、球体的结构特征对几何体进行分类.
解:根据几何体和柱体、椎体、台体、球体的结构特征得,
(1)(8)为球体,(2)为圆柱体,(3)为圆锥体
(4)为圆台体,(5)为棱锥体,(6)为棱柱体,(7)为两棱锥的组合体.
【点睛】考查柱体,椎体,台体,球体的几何特征,掌握它们的几何特征是解题的关键.
13.【考点】认识立体图形
【分析】结合已知三棱柱、四棱柱和五棱柱的特点,可知n棱柱一定有(n+2)个面,2n个顶点和3n条棱.
解:(1)四棱柱有8个顶点,12条棱,6个面;
(2)五棱柱有10个顶点,15条棱,7个面;
(3)六棱柱有12个顶点,18条棱,8个面;
七棱柱有14个顶点,21条棱,9个面;
(4)n棱柱有(n+2)个面,2n个顶点和3n条棱。
【点睛】考查了棱柱的特征,一般规律为:棱柱有个面,个顶点,条棱.
14.【考点】认识立体图形
【分析】(1)根据正五棱柱的特征即可答案;
(2)根据长方形的面积公式即可求得制作侧面共需要的材料.
解:这个笔筒共有6个面,其中一个底面是正五边形,五个侧面分别为长方形,
上底面与下底面各有5条棱,侧面有5条棱,共有15条棱;
(2)侧面共有5个长这6cm,宽为5cm的长方形,
6×5×5=150cm2,
答:制作侧面共用去150cm2材料.
【点睛】本题考查了认识立体图形,了解正五棱柱的特征是解本题的关键.
15.【考点】认识立体图形
【分析】(1)第1个图有1层,共1个小正方形,第2个图有2层,第2层正方形的个数为,根据相应规律可得第3层,第4层正方体的个数;
(2)根据随的变化而变化,即可判断出自变量和因变量;
(3)依据(1)得到的规律可得第层正方体的个数,进而得到时的值.
解:(1)∵第1个图有1层,共1个小正方体,
第2个图有2层,第2层正方体的个数为1+2=3,
第3个图有3层,第3层正方体的个数为1+2+3=6,
∴n=4时,即第4层正方体的个数为:1+2+3+4=10,
故答案为:6,10;
(2)S随n的变化而变化,n是自变量,S是因变量
(3)第n层时,s=1+2+3+…+n=n(n+1),
当n=10时,S=×10×11=55.
【点睛】本题考查图象规律性的变化:得到第层正方体的个数的规律是解决本题的关键.
姓名:__________班级:__________考号:__________
一 、选择题
1.在如图所示可爱的小猫图案中,没有用到的图形是
A. 长方形 B. 三角形 C. 八边形 D. 五边形
2.下列各组图形都是平面图形的一组是( )
A. 线段、圆、圆锥、球 B. 角、三角形、长方形、圆柱
C. 长方体、圆柱、棱锥、球 D. 角、三角形、正方形、圆
3.判断下列语句错误的是( )
A. 棱柱、球是立体图形,角、直线、三角形、圆是平面图形
B. 两点的所有连线中,线段最短
C. 经过平面上任意两点有且只有两条直线
D. 把一条射线绕着它的端点旋转而形成的图形叫做角
4.以下几种图形:
①三角形;②正方体;③圆;④圆锥;⑤圆柱;⑥正方形;⑦梯形;⑧球;⑨等腰三角形;
其中不属于平面图形的是( )
A. ②③④⑧ B. ②④⑤ C. ④⑤⑧⑨ D. ②④⑤⑧
5.如图所示的几何体的面数是( )
A. 3 B. 4 C. 5 D. 6
6.在八面体顶点数V、面数F、棱数E中,V+F-E=( )
A. 16 B. 6 C. 4 D. 2
二 、填空题
7.六棱柱是一个立体图形,它是由_____个面,_____条棱,_____个顶点组成的.
8.一个正六棱柱模型,它的上、下底面的形状、大小都相同,底面边长都是,侧棱长,则它的所有侧面的面积之和为________.
9.在下图所示立体图形中,(1)球体有____;(2)柱体有____;(3)锥体有____.
10.若正方体棱长的和是36,则它的体积是____.
11.一个正方体的表面涂满了同种颜色,按如图所示将它切成个大小相等的小立方块.设其中仅有个面涂有颜色的小立方块的个数为,则、、之间的数量关系为________.
三 、解答题
12.请给以下各图分类.
13.如图,左面的几何体叫三棱柱,它有五个面,条棱,个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
四棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
14.小明爱好手工制作,星期天小明纸板制作了一个正五棱柱的笔筒,它的底面边长是5厘米,侧棱长是6厘米,回答下列问题:
(1)这个笔筒一共有多少个面?多少条棱?
(2)制作侧面共用去多少材料?
15.棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.
(1)完成下表:
n
1
2
3
4
…
S
1
3
_____
_____
…
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.
答案解析
一 、选择题
1.【考点】认识立体图形
【分析】观察图形即可解答.
解:由图可知,构成小猫图案的图形有:三角形、圆、长方形,五边形和六边形.
∴在上述四个选项所涉及的图形中,只有八边形在小猫图案中没有用到.
故选C.
【点睛】本题考查了图形的识别,仔细观察图形是解决本题的关键.
2.【考点】平面图形
【分析】根据平面图形定义:一个图形的各部分都在同一个平面内的图形是平面图形可得答案.
解:A、线段、圆、圆锥、球中,圆锥、球不是平面图形,故此选项错误;
B、角、三角形、长方形、圆柱中,圆柱不是平面图形,故此选项错误;
C、长方体、圆柱、棱锥、球中都不是平面图形,故此选项错误;
D、角、三角形、正方形、圆都是平面图形,故此选项正确;
所以D选项是正确的.
【点睛】此题主要考查了平面图形,关键是掌握平面图形的定义.
3.【考点】认识立体图形
【分析】根据立体图形的认识,线段的性质,直线的性质,角的概念即可作出选择.
解:A、棱柱、球是立体图形,角、直线、三角形、圆是平面图形是正确的,不符合题意;
B、两点的所有连线中,线段最短是正确的,不符合题意;
C、经过平面上任意两点有且只有一条直线,原来的说法是错误的,符合题意;
D、把一条射线绕着它的端点旋转而形成的图形叫做角是正确的,不符合题意.
故选:C.
【点睛】考查了立体图形的认识,线段的性质,直线的性质,角的概念,是基础题型,关键是熟练掌握相关的知识.
4.【考点】平面图形
【分析】平面图形定义:一个图形的各部分都在同一个平面内,如:线段、 角、 三角形、 正方形、 圆等.
解:1三角形、3圆、6正方形、7梯形、9等腰三角形都是平面图形.
2正方体、4圆锥、5圆柱、8球都是立体图形.
综上所述,不属于平面图形的是:2 4 5 8.
所以D选项是正确的.
【点睛】本题考查立体图形的定义,要注意与平面图形的区分.
5.【考点】认识立体图形
【分析】根据几何的特点,面有底面和侧面.
解:如图所示的几何体的面数是5.
故选:C
【点睛】本题考核知识点:几何体的面. 解题关键点:理解几何体的特点.
6.【考点】认识立体图形
【分析】根据八面体的结构特征进行求解即可得.
解:如图,可知八面体顶点数V=6、面数F=8、棱数E=12,
所以V+F-E=6+8-12=2,
故选D.
【
点睛】本题考查了多面体的顶点数V、面数F、棱数E间的关系,仔细观察图形是解题的关键.
二 、填空题
7.【考点】认识立体图形
【分析】根据六棱柱的概念和定义进行解答即可得.
解:如图,六棱柱上下两个底面是6边形,侧面是6个长方形,
所以共有8个面,18条棱,12个顶点,
故答案为:8,18,12.
【点睛】本题考查了认识立体图形,解决本题的关键是掌握六棱柱的构造特点.
8.【考点】认识立体图形
【分析】对题意进行分析,结合正六棱柱的性质,即可求得答案.
解:正六棱柱的侧面有六个小长方形组成,长方形的长为5cm,宽为4cm,
故侧面面积S=6×5×4=120cm2.
故答案为:120cm2.
【点睛】考查了正六棱柱的侧面展开图和面积的求法,解答此题的关键是掌握六棱柱的展开图.
9.【考点】认识立体图形
【分析】根据球体,柱体,锥体的特点进行分类即可. 空间中到定点的距离等于定长的所有点组成的图形叫做球,球体是一个连续曲面的立体图形,由球面围成的几何体称为球体;柱体:一个多面体有两个面互相平行且大小相同,余下的每个相邻两个面的交线互相平行,这样的多面体称为柱; 圆锥和棱锥这样的立体图形是锥体
解:在下图所示立体图形中,(1)球体有⑦;(2)柱体有①③⑤;(3)锥体有②④⑥.
故答案为:(1). ⑦ (2). ①③⑤ (3). ②④⑥
【点睛】本题考核知识点:认识几何体.解题关键点:认识常见几何体的特点.
10.【考点】认识立体图形
【分析】首先用棱长总和除以12求出棱长,再根据正方体的体积公式,把数据代入公式解答.
解:36÷12=3,
V=a3=3×3×3=27,
它的体积是27.
【点睛】本题考查的是正方体的体积公式,熟练掌握这一点是解题的关键.
11.【考点】认识立体图形
【分析】根据题图分别找出3个面,2个面,1个面涂有颜色的正方体即可.
解:由题图可知:在原正方体的8个顶点处的8个小正方体上,有3个面涂有颜色;2个面涂有颜色的小正方体有12个,1个面涂有颜色的小正方体有6个,
则6﹣12+8=2.
故答案为:.
【点睛】本题主要考查认识立体几何图形,根据已知得出涂有颜色不同的小立方体的个数是解题关键.
三 、解答题
12.【考点】认识立体图形
【分析】主要根据几何体和柱体、椎体、台体、球体的结构特征对几何体进行分类.
解:根据几何体和柱体、椎体、台体、球体的结构特征得,
(1)(8)为球体,(2)为圆柱体,(3)为圆锥体
(4)为圆台体,(5)为棱锥体,(6)为棱柱体,(7)为两棱锥的组合体.
【点睛】考查柱体,椎体,台体,球体的几何特征,掌握它们的几何特征是解题的关键.
13.【考点】认识立体图形
【分析】结合已知三棱柱、四棱柱和五棱柱的特点,可知n棱柱一定有(n+2)个面,2n个顶点和3n条棱.
解:(1)四棱柱有8个顶点,12条棱,6个面;
(2)五棱柱有10个顶点,15条棱,7个面;
(3)六棱柱有12个顶点,18条棱,8个面;
七棱柱有14个顶点,21条棱,9个面;
(4)n棱柱有(n+2)个面,2n个顶点和3n条棱。
【点睛】考查了棱柱的特征,一般规律为:棱柱有个面,个顶点,条棱.
14.【考点】认识立体图形
【分析】(1)根据正五棱柱的特征即可答案;
(2)根据长方形的面积公式即可求得制作侧面共需要的材料.
解:这个笔筒共有6个面,其中一个底面是正五边形,五个侧面分别为长方形,
上底面与下底面各有5条棱,侧面有5条棱,共有15条棱;
(2)侧面共有5个长这6cm,宽为5cm的长方形,
6×5×5=150cm2,
答:制作侧面共用去150cm2材料.
【点睛】本题考查了认识立体图形,了解正五棱柱的特征是解本题的关键.
15.【考点】认识立体图形
【分析】(1)第1个图有1层,共1个小正方形,第2个图有2层,第2层正方形的个数为,根据相应规律可得第3层,第4层正方体的个数;
(2)根据随的变化而变化,即可判断出自变量和因变量;
(3)依据(1)得到的规律可得第层正方体的个数,进而得到时的值.
解:(1)∵第1个图有1层,共1个小正方体,
第2个图有2层,第2层正方体的个数为1+2=3,
第3个图有3层,第3层正方体的个数为1+2+3=6,
∴n=4时,即第4层正方体的个数为:1+2+3+4=10,
故答案为:6,10;
(2)S随n的变化而变化,n是自变量,S是因变量
(3)第n层时,s=1+2+3+…+n=n(n+1),
当n=10时,S=×10×11=55.
【点睛】本题考查图象规律性的变化:得到第层正方体的个数的规律是解决本题的关键.
