4.1.2 点、线、面、体形课时作业
图片预览


文档简介
4.1.2 点、线、面、体形课时作业
姓名:__________班级:__________考号:__________
一 、选择题
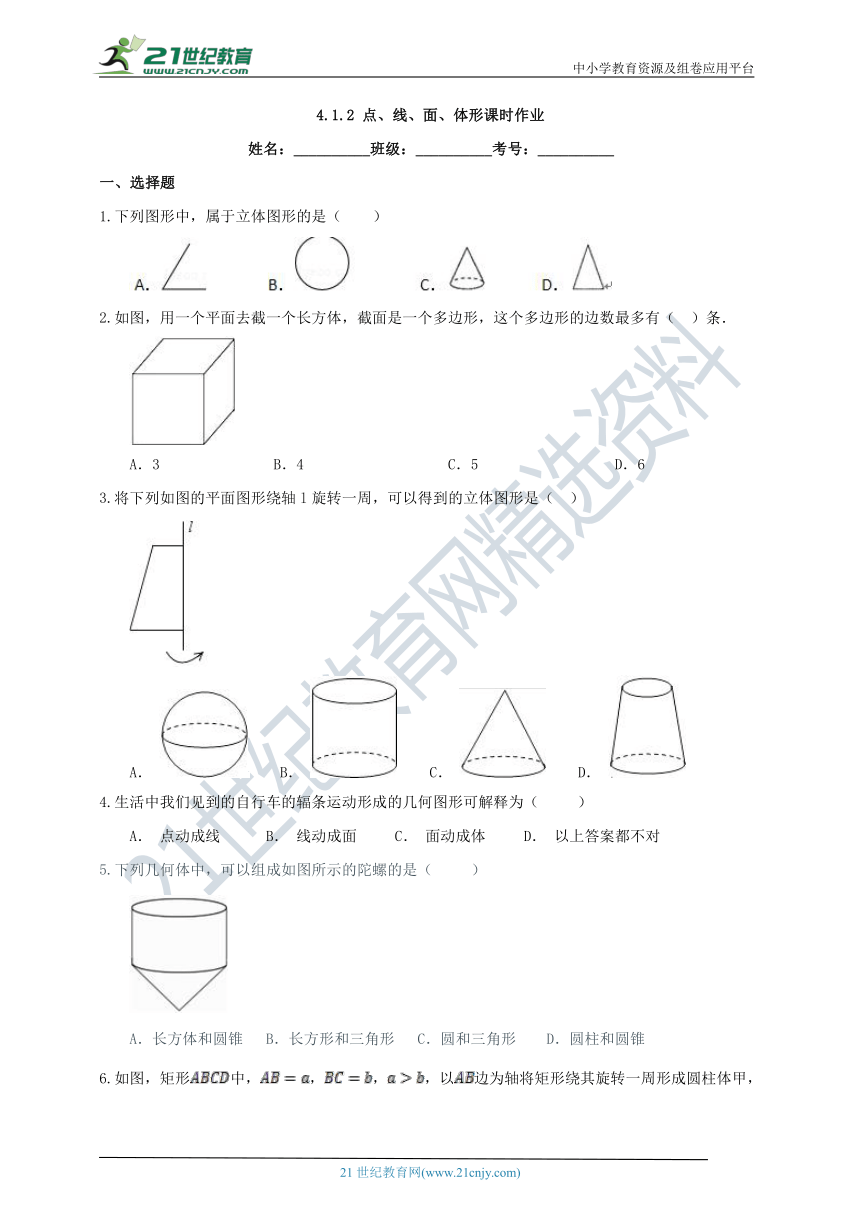
1.下列图形中,属于立体图形的是( )
2.如图,用一个平面去截一个长方体,截面是一个多边形,这个多边形的边数最多有( )条. A.3 B.4 C.5 D.6
3.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
4.生活中我们见到的自行车的辐条运动形成的几何图形可解释为( )
A. 点动成线 B. 线动成面 C. 面动成体 D. 以上答案都不对
5.下列几何体中,可以组成如图所示的陀螺的是( ) A.长方体和圆锥 B.长方形和三角形 C.圆和三角形 D.圆柱和圆锥
6.如图,矩形中,,,,以边为轴将矩形绕其旋转一周
形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为、,侧面积分别为、,则下列式子正确的是( )
A., B.,
C., D. ,
二 、填空题
7.中国武术中有“枪扎一条线,棍扫一大片”这样的说法,这句话给我们以_____的形象.
8.直角三角形的两直角边长分别为 8cm、6cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是_____.
9.时钟秒针旋转时,形成一个圆面,这说明了______________;三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了______________.
10.直角三角形绕着它的一条直角边所在直线旋转360°形成的几何体是_____.
11.用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 .
三 、解答题
12.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为8 cm,宽为6 cm的长方形,绕它的一条边所在的直线旋转一周后,你能计算出所得到的圆柱体的体积吗?(结果保留π)
13.已知长方形的长为.宽为,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留)
14.如图所示,画一个长和宽分别为、的长方形,并将其按一定的方式进行旋转.
你能得到几种不同的圆柱体?
把一个平面图形旋转成几何体,必须明确哪两个条件?
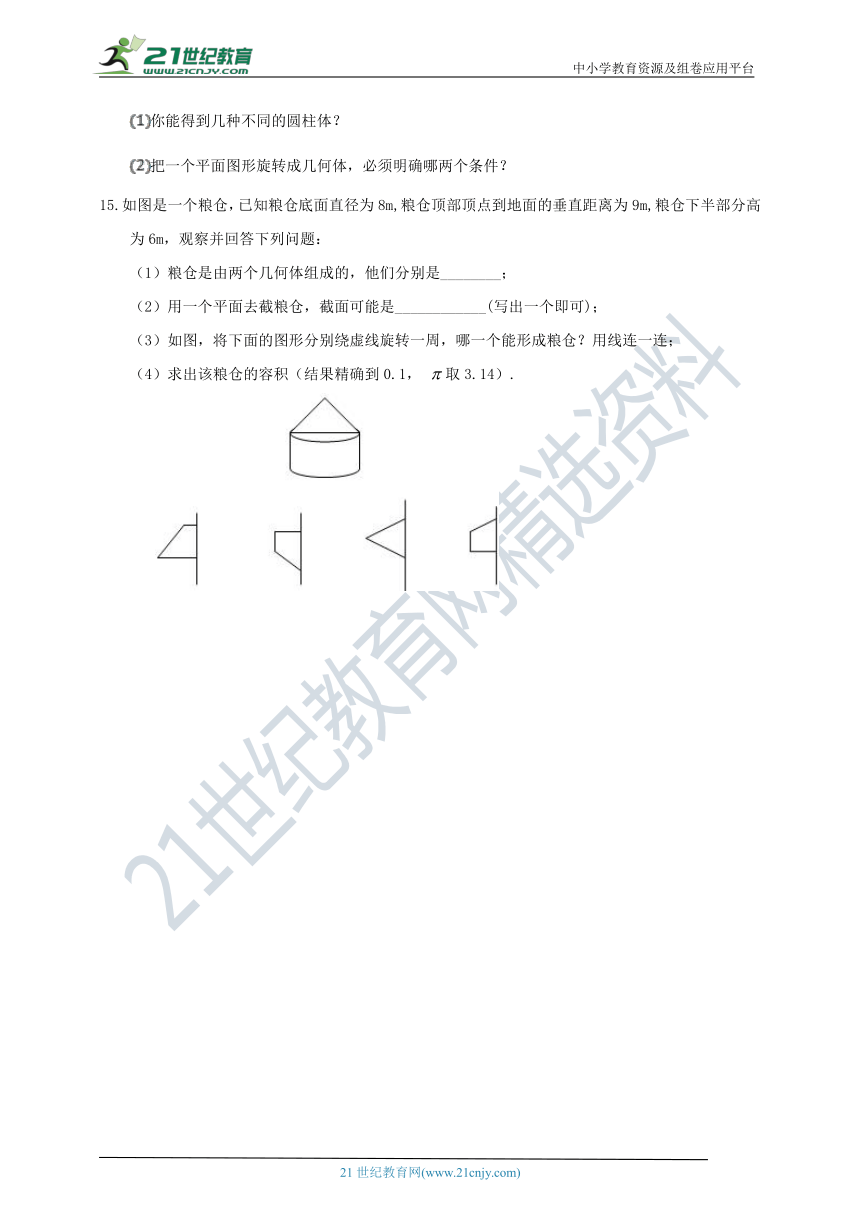
15.如图是一个粮仓,已知粮仓底面直径为8m,粮仓顶部顶点到地面的垂直距离为9m,粮仓下半部分高为6m,观察并回答下列问题:
(1)粮仓是由两个几何体组成的,他们分别是________;
(2)用一个平面去截粮仓,截面可能是____________(写出一个即可);
(3)如图,将下面的图形分别绕虚线旋转一周,哪一个能形成粮仓?用线连一连;
(4)求出该粮仓的容积(结果精确到0.1, 取3.14).
答案解析
一 、选择题
1.【考点】认识立体图形.
【分析】根据平面图形所表示的各个部分都在同一平面内,立体图形是各部分不在同一平面内的几何,由一个或多个面围成的可以存在于现实生活中的三维图形,可得答案.
解:A、角是平面图形,故A错误;
B、圆是平面图形,故B错误;
C、圆锥是立体图形,故C正确;
D、三角形是平面图形,故D错误.
故选:C.
2.【考点】截一个几何体
【分析】长方体的截面,最多可以经过6个面,所以边数最多的截面是六边形. 解:长方体的截面中,边数最多的多边形是六边形,即多边形的边数最多有6条. 故选D
3.【考点】点、线、面、体
【分析】平面图形为直角梯形,根据面动成体,直角梯形绕高旋转得到圆台,即可得出结论.
解:直角梯形绕直线l旋转一周,可以得到圆台.
故答案为:D.
【点睛】本题考查了点、线、面、体及之间的联系.根据根据面动成体,直角梯形绕高旋转得到圆台,注意直角梯形绕不同的边旋转,得到的立体图形不同.
4.【考点】点、线、面、体
【分析】根据从运动的观点来看点动成线,线动成面,面动成体,
解:生活中我们见到的自行车的辐条运动形成的几何图形可解释为:线动成面,
故选:B.
【点睛】此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
5.【考点】点、线、面、体
【分析】图中的几何体上面是圆柱,下面是圆锥,都是旋转体,圆柱是由长方形旋转而成的,圆锥是由三角形旋转而成的,由此得出答案. 解:如图所示的陀螺的是由长方形和三角形旋转而成的. 故选:B.
6.【考点】点、线、面、体
【分析】用含a、b的式子表示、、、,再根据a>b进行差的符号;
解:根据圆柱的体积=底面积×高,侧面积=底边周长×高,得
所以 ,
又因为a>b,所以<0,
所以,
二 、填空题
7.【考点】点、线、面、体
【分析】根据几何图形中的点、线、面的关系即可求得答案.
解:枪尖可看成是点,棍可看成一条线,
∴可以看成是点动成线、线动成面,
故答案为:点动成线、线动成面.
【点睛】本题主要考查点、线、面、体的关系,掌握点动成线、线动成面、面动成体是解题的关键.
8.【考点】点、线、面、体
【分析】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为8或6cm,根据圆的面积公式进行计算即可.
解:若绕着8cm的直角边所在的直线进行旋转,则底面半径为6cm,底面面积为36πcm2,
若绕着6cm的直角边所在的直线进行旋转,则底面半径为8cm,底面面积为64πcm2,
故答案为:64πcm2或36πcm2.
【点睛】本题考查了点、线、面、体,解答此题的关键是:能够想象出所得的立体图形的形状和特征,能灵活运用圆的面积公式进行解答.注意底面半径有两种情况.
9.【考点】点、线、面、体
【分析】熟悉点、线、面、体之间的联系,根据运动的观点即可解.
解:根据分析即知:点动成线;线动成面;面动成体.
故答案为:点动成线;线动成面;面动成体.
【点睛】本题考查了点、线、面、体之间的联系,点是构成图形的最基本元素.
10.【考点】点、线、面、体
【分析】本题是一个直角三角形围绕一条直角边为中心对称轴旋转一周根据面动成体的原理即可解.
解:直角三角形绕它的直角边旋转一周可形成圆锥.
故答案为:圆锥.
【点睛】此题考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
11.【考点】截一个几何体
【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
解:长方体沿体面对角线截几何体可以截出三角形;
五棱柱沿顶点截几何体可以截得三角形;
圆柱不能截出三角形;
圆锥沿顶点可以截出三角形.
故不能截出三角形的几何体是圆柱.
故答案为:圆柱.
三 、解答题
12.【考点】点、线、面、体
【分析】分两种情况讨论,①若绕着长所在的直线旋转,②若绕着宽所在的直线旋转,分别计算出圆柱的体积即可.
解:①若绕着长所在的直线旋转,所得图形为圆柱,
此时底面圆半径为6cm,圆柱的高为8cm,
则V=π×62×8=288πcm3;
②若绕着宽所在的直线旋转,所得图形为圆柱,
此时底面圆半径为8cm,圆柱的高为6cm,
则V=π×82×6=384πcm3.
答:所得到的圆柱体的体积为288π cm3或384π cm3
【点睛】本题考查了面动成体的知识,知道矩形绕一边旋转后得到的图形是圆柱是关键,另外要注意分情况讨论,不要漏解.
13.【考点】点、线、面、体
【分析】分以长为轴旋转所得圆柱和以宽为轴旋转所得圆柱两种情况求解即可.
解: (1)情况①, 情况②,
(2)情况①, 情况②,
【点睛】本题考查圆柱体的体积和表面积的求法,一定要注意分情况讨论.
14.【考点】点、线、面、体
【分析】(1)分别以长方形的长和宽所在直线为旋转轴,旋转360°;以对边的中点连线所在直线为旋转轴,旋转180°;
(2)需要说明旋转轴和旋转角这两个条件.
解:由于长和宽分别为、的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长(或)所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
②一长方形的一条宽(或)所在直线为旋转轴,旋转一周,可得到底面半径为,高为的圆柱体;
③以长方形的长、的中点、所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
④以长方形的长、的中点、所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
【点睛】本题考查了点、线、面、体,解题的关键是根据题意分情况讨论与熟练的掌握旋转成几何体的条件.
15.【考点】点、线、面、体
【分析】(1)由简单几何体的概念即可解答;
(2)用一个平面去截圆锥或圆柱,都可以得到一个圆,即可解答;
(3)根据圆柱和圆锥的定义,即可解答此题;
(4)粮仓体积分为圆柱和圆锥两部分计算体积.
解:(1)粮仓上半部分是圆锥,下半部分是圆柱,
故答案为:圆柱和圆锥;
(2)用一个平面去截圆锥或圆柱,都可以得到一个圆,
故答案为:圆;
(3)连线如下:
(4)粮仓的体积为3.14×42×6+3.14×42×3×=351.7m3.
【点睛】此题考查了点动成线、线动成面、面动成体的原则以及圆柱、圆锥的体积计算,解题的关键是熟记圆柱圆锥的体积公式.
姓名:__________班级:__________考号:__________
一 、选择题
1.下列图形中,属于立体图形的是( )
2.如图,用一个平面去截一个长方体,截面是一个多边形,这个多边形的边数最多有( )条. A.3 B.4 C.5 D.6
3.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A. B. C. D.
4.生活中我们见到的自行车的辐条运动形成的几何图形可解释为( )
A. 点动成线 B. 线动成面 C. 面动成体 D. 以上答案都不对
5.下列几何体中,可以组成如图所示的陀螺的是( ) A.长方体和圆锥 B.长方形和三角形 C.圆和三角形 D.圆柱和圆锥
6.如图,矩形中,,,,以边为轴将矩形绕其旋转一周
形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为、,侧面积分别为、,则下列式子正确的是( )
A., B.,
C., D. ,
二 、填空题
7.中国武术中有“枪扎一条线,棍扫一大片”这样的说法,这句话给我们以_____的形象.
8.直角三角形的两直角边长分别为 8cm、6cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是_____.
9.时钟秒针旋转时,形成一个圆面,这说明了______________;三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了______________.
10.直角三角形绕着它的一条直角边所在直线旋转360°形成的几何体是_____.
11.用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 .
三 、解答题
12.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为8 cm,宽为6 cm的长方形,绕它的一条边所在的直线旋转一周后,你能计算出所得到的圆柱体的体积吗?(结果保留π)
13.已知长方形的长为.宽为,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留)
14.如图所示,画一个长和宽分别为、的长方形,并将其按一定的方式进行旋转.
你能得到几种不同的圆柱体?
把一个平面图形旋转成几何体,必须明确哪两个条件?
15.如图是一个粮仓,已知粮仓底面直径为8m,粮仓顶部顶点到地面的垂直距离为9m,粮仓下半部分高为6m,观察并回答下列问题:
(1)粮仓是由两个几何体组成的,他们分别是________;
(2)用一个平面去截粮仓,截面可能是____________(写出一个即可);
(3)如图,将下面的图形分别绕虚线旋转一周,哪一个能形成粮仓?用线连一连;
(4)求出该粮仓的容积(结果精确到0.1, 取3.14).
答案解析
一 、选择题
1.【考点】认识立体图形.
【分析】根据平面图形所表示的各个部分都在同一平面内,立体图形是各部分不在同一平面内的几何,由一个或多个面围成的可以存在于现实生活中的三维图形,可得答案.
解:A、角是平面图形,故A错误;
B、圆是平面图形,故B错误;
C、圆锥是立体图形,故C正确;
D、三角形是平面图形,故D错误.
故选:C.
2.【考点】截一个几何体
【分析】长方体的截面,最多可以经过6个面,所以边数最多的截面是六边形. 解:长方体的截面中,边数最多的多边形是六边形,即多边形的边数最多有6条. 故选D
3.【考点】点、线、面、体
【分析】平面图形为直角梯形,根据面动成体,直角梯形绕高旋转得到圆台,即可得出结论.
解:直角梯形绕直线l旋转一周,可以得到圆台.
故答案为:D.
【点睛】本题考查了点、线、面、体及之间的联系.根据根据面动成体,直角梯形绕高旋转得到圆台,注意直角梯形绕不同的边旋转,得到的立体图形不同.
4.【考点】点、线、面、体
【分析】根据从运动的观点来看点动成线,线动成面,面动成体,
解:生活中我们见到的自行车的辐条运动形成的几何图形可解释为:线动成面,
故选:B.
【点睛】此题主要考查了点、线、面、体,关键是掌握四者之间的关系.
5.【考点】点、线、面、体
【分析】图中的几何体上面是圆柱,下面是圆锥,都是旋转体,圆柱是由长方形旋转而成的,圆锥是由三角形旋转而成的,由此得出答案. 解:如图所示的陀螺的是由长方形和三角形旋转而成的. 故选:B.
6.【考点】点、线、面、体
【分析】用含a、b的式子表示、、、,再根据a>b进行差的符号;
解:根据圆柱的体积=底面积×高,侧面积=底边周长×高,得
所以 ,
又因为a>b,所以<0,
所以,
二 、填空题
7.【考点】点、线、面、体
【分析】根据几何图形中的点、线、面的关系即可求得答案.
解:枪尖可看成是点,棍可看成一条线,
∴可以看成是点动成线、线动成面,
故答案为:点动成线、线动成面.
【点睛】本题主要考查点、线、面、体的关系,掌握点动成线、线动成面、面动成体是解题的关键.
8.【考点】点、线、面、体
【分析】旋转后得到的几何体为圆锥,圆锥的底面为圆,半径为8或6cm,根据圆的面积公式进行计算即可.
解:若绕着8cm的直角边所在的直线进行旋转,则底面半径为6cm,底面面积为36πcm2,
若绕着6cm的直角边所在的直线进行旋转,则底面半径为8cm,底面面积为64πcm2,
故答案为:64πcm2或36πcm2.
【点睛】本题考查了点、线、面、体,解答此题的关键是:能够想象出所得的立体图形的形状和特征,能灵活运用圆的面积公式进行解答.注意底面半径有两种情况.
9.【考点】点、线、面、体
【分析】熟悉点、线、面、体之间的联系,根据运动的观点即可解.
解:根据分析即知:点动成线;线动成面;面动成体.
故答案为:点动成线;线动成面;面动成体.
【点睛】本题考查了点、线、面、体之间的联系,点是构成图形的最基本元素.
10.【考点】点、线、面、体
【分析】本题是一个直角三角形围绕一条直角边为中心对称轴旋转一周根据面动成体的原理即可解.
解:直角三角形绕它的直角边旋转一周可形成圆锥.
故答案为:圆锥.
【点睛】此题考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
11.【考点】截一个几何体
【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
解:长方体沿体面对角线截几何体可以截出三角形;
五棱柱沿顶点截几何体可以截得三角形;
圆柱不能截出三角形;
圆锥沿顶点可以截出三角形.
故不能截出三角形的几何体是圆柱.
故答案为:圆柱.
三 、解答题
12.【考点】点、线、面、体
【分析】分两种情况讨论,①若绕着长所在的直线旋转,②若绕着宽所在的直线旋转,分别计算出圆柱的体积即可.
解:①若绕着长所在的直线旋转,所得图形为圆柱,
此时底面圆半径为6cm,圆柱的高为8cm,
则V=π×62×8=288πcm3;
②若绕着宽所在的直线旋转,所得图形为圆柱,
此时底面圆半径为8cm,圆柱的高为6cm,
则V=π×82×6=384πcm3.
答:所得到的圆柱体的体积为288π cm3或384π cm3
【点睛】本题考查了面动成体的知识,知道矩形绕一边旋转后得到的图形是圆柱是关键,另外要注意分情况讨论,不要漏解.
13.【考点】点、线、面、体
【分析】分以长为轴旋转所得圆柱和以宽为轴旋转所得圆柱两种情况求解即可.
解: (1)情况①, 情况②,
(2)情况①, 情况②,
【点睛】本题考查圆柱体的体积和表面积的求法,一定要注意分情况讨论.
14.【考点】点、线、面、体
【分析】(1)分别以长方形的长和宽所在直线为旋转轴,旋转360°;以对边的中点连线所在直线为旋转轴,旋转180°;
(2)需要说明旋转轴和旋转角这两个条件.
解:由于长和宽分别为、的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长(或)所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
②一长方形的一条宽(或)所在直线为旋转轴,旋转一周,可得到底面半径为,高为的圆柱体;
③以长方形的长、的中点、所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
④以长方形的长、的中点、所在直线为旋转轴,旋转,可得到底面半径为,高为的圆柱体;
把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
【点睛】本题考查了点、线、面、体,解题的关键是根据题意分情况讨论与熟练的掌握旋转成几何体的条件.
15.【考点】点、线、面、体
【分析】(1)由简单几何体的概念即可解答;
(2)用一个平面去截圆锥或圆柱,都可以得到一个圆,即可解答;
(3)根据圆柱和圆锥的定义,即可解答此题;
(4)粮仓体积分为圆柱和圆锥两部分计算体积.
解:(1)粮仓上半部分是圆锥,下半部分是圆柱,
故答案为:圆柱和圆锥;
(2)用一个平面去截圆锥或圆柱,都可以得到一个圆,
故答案为:圆;
(3)连线如下:
(4)粮仓的体积为3.14×42×6+3.14×42×3×=351.7m3.
【点睛】此题考查了点动成线、线动成面、面动成体的原则以及圆柱、圆锥的体积计算,解题的关键是熟记圆柱圆锥的体积公式.
