十字交叉法在化学计算中的应用[下学期]
图片预览
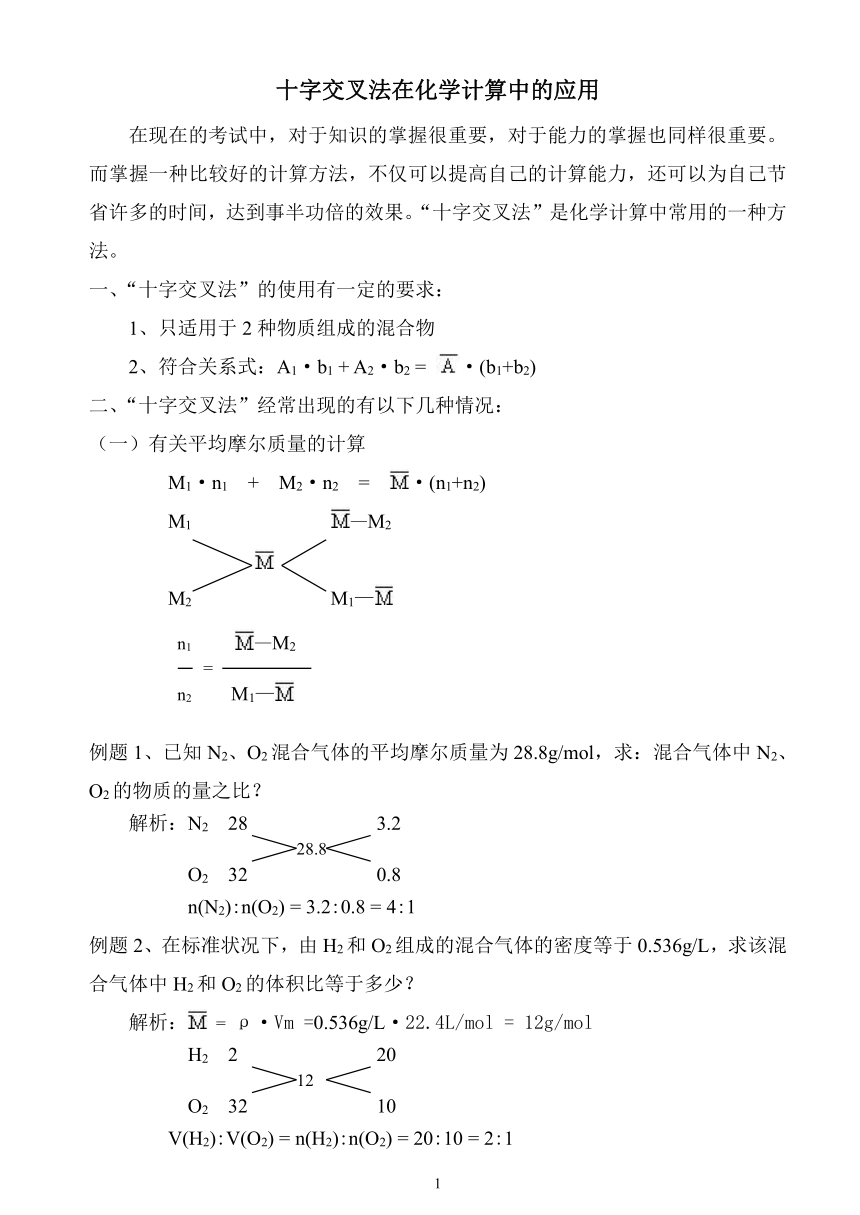

文档简介
十字交叉法在化学计算中的应用
在现在的考试中,对于知识的掌握很重要,对于能力的掌握也同样很重要。而掌握一种比较好的计算方法,不仅可以提高自己的计算能力,还可以为自己节省许多的时间,达到事半功倍的效果。“十字交叉法”是化学计算中常用的一种方法。
一、“十字交叉法”的使用有一定的要求:
1、 只适用于2种物质组成的混合物
2、 符合关系式:A1·b1 + A2·b2 = ·(b1+b2)
二、“十字交叉法”经常出现的有以下几种情况:
(一)有关平均摩尔质量的计算
M1·n1 + M2·n2 = ·(n1+n2)
M1 —M2
M2 M1—
例题1、已知N2、O2混合气体的平均摩尔质量为28.8g/mol,求:混合气体中N2、O2的物质的量之比?
解析:N2 28 3.2
28.8
O2 32 0.8
n(N2):n(O2) = 3.2:0.8 = 4:1
例题2、在标准状况下,由H2和O2组成的混合气体的密度等于0.536g/L,求该混合气体中H2和O2的体积比等于多少?
解析: = ρ·Vm =0.536g/L·22.4L/mol = 12g/mol
H2 2 20
12
O2 32 10
V(H2):V(O2) = n(H2):n(O2) = 20:10 = 2:1
(二)同位素原子的个数比
例题3:已知自然界中铱有两种质量数分别为191和193的同位素,而铱的平均原子量为192.22,则这两位种同位素的原子个数比
A、39:61 B、61:39 C、1:1 D、39:11
解析:191Ir 191 0.78
192.22
193Ir 193 1.22
n(191Ir):n(191Ir) = 0.78:1.22 = 39:61
答案:A
(三)利用对于反应的比较求物质的量之比
例题4、用1L浓度为1.0mol/L的NaOH溶液吸收了0.80mol CO2气体,所得溶液中CO32—和HCO3—的物质的量之比为: 。
解析:2OH— + CO2 == CO32— + H2O
OH— + CO2 == HCO3—
平均每摩尔CO2吸收的OH—的物质的量为:1.0mol/0.80=1.25mol
CO32— 2 0.25
1.25
HCO3— 1 0.75
n(CO32—):n(HCO3—) = 0.25:0.75 = 1:3
例题5、已知下列热化学方程式:
C(s) +O2(g) == CO2(g);ΔH=-393.2kJ/mol
2H2(g) + O2(g) == 2H2O(g);ΔH=-483.6kJ/mol
现有0.2mol的炭粉和氢气组成的悬浮气、固混合物在氧气中完全燃烧,共放出63.5kJ热量,则炭粉和氢气的物质的量之比为:
A、1:1 B、1:2 C、2:3 D、3:2
解析:平均每摩尔物质放出的热量为:
63.5kJ/0.2mol=317.5kJ/mol
CO2 393.2 75.7
317.5
H2 241.8 75.7
n(CO2):n(H2) = 75.7:75.7 = 1:1
答案:A
例题6、现有100克碳酸镁和碳酸钡的混和物,它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。求混和物中碳酸镁和碳酸钡的物质的量之比。
解析:MgCO3 + 2HCl ==MgCl2 + H2O + CO2↑
BaCO3 + 2HCl ==BaCl2 + H2O + CO2↑
CaCO3 + 2HCl ==CaCl2 + H2O + CO2↑
可将碳酸钙的式量理解为碳酸镁和碳酸钡混和物的平均式量,等于100。
MgCO3 84 97
100
BaCO3 197 16
n(MgCO3):n(BaCO3) = 97:16
(四)关于溶液的质量分数的计算
m1·ω1 + m2·ω2 = (m1+m2)·ω3
例题7、现有20%和5%的两种盐酸溶液,若要配制15%的盐酸溶液,两种盐酸溶液的质量比为多少?
解析:20%HCl 20 10
15
5%HCl 5 5
m(20%HCl):m(5%HCl) = 10:5 = 2:1
(五)关于溶液的物质的量浓度的计算(若溶液混合体积可以相加)
c1·V1 + c2·V2 = c3·(V1+V2)
例题8、物质的量浓度分别为6mol/L和1mol/L的硫酸溶液,按怎样的体积比混合才能配成4mol/L的溶液
解析:6mol/L H2SO4 6 3
4
1mol/L H2SO4 1 2
V(6mol/L H2SO4):V(1mol/L H2SO4) = 3:2
十字交叉法是进行二组分混和物平均量与组分量计算的一种简便方法。凡可按M1n1 + M2n2 = (n1 + n2)计算的问题,均可用十字交叉法计算的问题,均可按十字交叉法计算,算式为:
M1 n1=(M2-)
M2 n2=(-M1)
式中,表示混和物的某平均量,M1、M2则表示两组分对应的量。如表示平均分子量,M1、M2则表示两组分各自的分子量,n1、n2表示两组分在混和物中所占的份额,n1:n2在大多数情况下表示两组分物质的量之比,有时也可以是两组分的质量比,如在进行有关溶液质量百分比浓度的计算。十字交叉法常用于求算:混和气体平均分子量及组成、混和烃平均分子式及组成、同位素原子百分含量、溶液的配制、混和物的反应等。
(一)混和气体计算中的十字交叉法
【例题】在常温下,将1体积乙烯和一定量的某气态未知烃混和,测得混和气体对氢气的相对密度为12,求这种烃所占的体积。
【分析】根据相对密度计算可得混和气体的平均式量为24,乙烯的式量是28,那么未知烃的式量肯定小于24,式量小于24的烃只有甲烷,利用十字交叉法可求得甲烷是0.5体积
(二)同位素原子百分含量计算的十字叉法
【例题】溴有两种同位素,在自然界中这两种同位素大约各占一半,已知溴的原子序数是35,原子量是80,则溴的两种同位素的中子数分别等于。
(A)79 、81 (B)45 、46 (C)44 、45 (D)44 、46
【分析】两种同位素大约各占一半,根据十字交叉法可知,两种同位素原子量与溴原子量的差值相等,那么它们的中子数应相差2,所以答案为D
(三)溶液配制计算中的十字交叉法
【例题】某同学欲配制40%的NaOH溶液100克,实验室中现有10%的NaOH溶液和NaOH固体,问此同学应各取上述物质多少克?
【分析】10%NaOH溶液溶质为10,NaOH固体溶质为100,40%NaOH溶液溶质为40,利用十字交叉法得:需10%NaOH溶液为
×100=66.7克,需NaOH固体为×100=33.3克
( 四)混和物反应计算中的十字交叉法
【例题】现有100克碳酸锂和碳酸钡的混和物,它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。计算混和物中碳酸锂和碳酸钡的物质的量之比。
【分析】可将碳酸钙的式量理解为碳酸锂和碳酸钡的混和物的平均式量,利用十字交叉法计算可得碳酸锂和碳酸钡的物质的量之比97:26
n1 —M2
=
n2 M1—
m1 ω3—ω2
=
m2 ω1—ω3
V1 c3—c2
=
V2 c1—c3
PAGE
2
在现在的考试中,对于知识的掌握很重要,对于能力的掌握也同样很重要。而掌握一种比较好的计算方法,不仅可以提高自己的计算能力,还可以为自己节省许多的时间,达到事半功倍的效果。“十字交叉法”是化学计算中常用的一种方法。
一、“十字交叉法”的使用有一定的要求:
1、 只适用于2种物质组成的混合物
2、 符合关系式:A1·b1 + A2·b2 = ·(b1+b2)
二、“十字交叉法”经常出现的有以下几种情况:
(一)有关平均摩尔质量的计算
M1·n1 + M2·n2 = ·(n1+n2)
M1 —M2
M2 M1—
例题1、已知N2、O2混合气体的平均摩尔质量为28.8g/mol,求:混合气体中N2、O2的物质的量之比?
解析:N2 28 3.2
28.8
O2 32 0.8
n(N2):n(O2) = 3.2:0.8 = 4:1
例题2、在标准状况下,由H2和O2组成的混合气体的密度等于0.536g/L,求该混合气体中H2和O2的体积比等于多少?
解析: = ρ·Vm =0.536g/L·22.4L/mol = 12g/mol
H2 2 20
12
O2 32 10
V(H2):V(O2) = n(H2):n(O2) = 20:10 = 2:1
(二)同位素原子的个数比
例题3:已知自然界中铱有两种质量数分别为191和193的同位素,而铱的平均原子量为192.22,则这两位种同位素的原子个数比
A、39:61 B、61:39 C、1:1 D、39:11
解析:191Ir 191 0.78
192.22
193Ir 193 1.22
n(191Ir):n(191Ir) = 0.78:1.22 = 39:61
答案:A
(三)利用对于反应的比较求物质的量之比
例题4、用1L浓度为1.0mol/L的NaOH溶液吸收了0.80mol CO2气体,所得溶液中CO32—和HCO3—的物质的量之比为: 。
解析:2OH— + CO2 == CO32— + H2O
OH— + CO2 == HCO3—
平均每摩尔CO2吸收的OH—的物质的量为:1.0mol/0.80=1.25mol
CO32— 2 0.25
1.25
HCO3— 1 0.75
n(CO32—):n(HCO3—) = 0.25:0.75 = 1:3
例题5、已知下列热化学方程式:
C(s) +O2(g) == CO2(g);ΔH=-393.2kJ/mol
2H2(g) + O2(g) == 2H2O(g);ΔH=-483.6kJ/mol
现有0.2mol的炭粉和氢气组成的悬浮气、固混合物在氧气中完全燃烧,共放出63.5kJ热量,则炭粉和氢气的物质的量之比为:
A、1:1 B、1:2 C、2:3 D、3:2
解析:平均每摩尔物质放出的热量为:
63.5kJ/0.2mol=317.5kJ/mol
CO2 393.2 75.7
317.5
H2 241.8 75.7
n(CO2):n(H2) = 75.7:75.7 = 1:1
答案:A
例题6、现有100克碳酸镁和碳酸钡的混和物,它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。求混和物中碳酸镁和碳酸钡的物质的量之比。
解析:MgCO3 + 2HCl ==MgCl2 + H2O + CO2↑
BaCO3 + 2HCl ==BaCl2 + H2O + CO2↑
CaCO3 + 2HCl ==CaCl2 + H2O + CO2↑
可将碳酸钙的式量理解为碳酸镁和碳酸钡混和物的平均式量,等于100。
MgCO3 84 97
100
BaCO3 197 16
n(MgCO3):n(BaCO3) = 97:16
(四)关于溶液的质量分数的计算
m1·ω1 + m2·ω2 = (m1+m2)·ω3
例题7、现有20%和5%的两种盐酸溶液,若要配制15%的盐酸溶液,两种盐酸溶液的质量比为多少?
解析:20%HCl 20 10
15
5%HCl 5 5
m(20%HCl):m(5%HCl) = 10:5 = 2:1
(五)关于溶液的物质的量浓度的计算(若溶液混合体积可以相加)
c1·V1 + c2·V2 = c3·(V1+V2)
例题8、物质的量浓度分别为6mol/L和1mol/L的硫酸溶液,按怎样的体积比混合才能配成4mol/L的溶液
解析:6mol/L H2SO4 6 3
4
1mol/L H2SO4 1 2
V(6mol/L H2SO4):V(1mol/L H2SO4) = 3:2
十字交叉法是进行二组分混和物平均量与组分量计算的一种简便方法。凡可按M1n1 + M2n2 = (n1 + n2)计算的问题,均可用十字交叉法计算的问题,均可按十字交叉法计算,算式为:
M1 n1=(M2-)
M2 n2=(-M1)
式中,表示混和物的某平均量,M1、M2则表示两组分对应的量。如表示平均分子量,M1、M2则表示两组分各自的分子量,n1、n2表示两组分在混和物中所占的份额,n1:n2在大多数情况下表示两组分物质的量之比,有时也可以是两组分的质量比,如在进行有关溶液质量百分比浓度的计算。十字交叉法常用于求算:混和气体平均分子量及组成、混和烃平均分子式及组成、同位素原子百分含量、溶液的配制、混和物的反应等。
(一)混和气体计算中的十字交叉法
【例题】在常温下,将1体积乙烯和一定量的某气态未知烃混和,测得混和气体对氢气的相对密度为12,求这种烃所占的体积。
【分析】根据相对密度计算可得混和气体的平均式量为24,乙烯的式量是28,那么未知烃的式量肯定小于24,式量小于24的烃只有甲烷,利用十字交叉法可求得甲烷是0.5体积
(二)同位素原子百分含量计算的十字叉法
【例题】溴有两种同位素,在自然界中这两种同位素大约各占一半,已知溴的原子序数是35,原子量是80,则溴的两种同位素的中子数分别等于。
(A)79 、81 (B)45 、46 (C)44 、45 (D)44 、46
【分析】两种同位素大约各占一半,根据十字交叉法可知,两种同位素原子量与溴原子量的差值相等,那么它们的中子数应相差2,所以答案为D
(三)溶液配制计算中的十字交叉法
【例题】某同学欲配制40%的NaOH溶液100克,实验室中现有10%的NaOH溶液和NaOH固体,问此同学应各取上述物质多少克?
【分析】10%NaOH溶液溶质为10,NaOH固体溶质为100,40%NaOH溶液溶质为40,利用十字交叉法得:需10%NaOH溶液为
×100=66.7克,需NaOH固体为×100=33.3克
( 四)混和物反应计算中的十字交叉法
【例题】现有100克碳酸锂和碳酸钡的混和物,它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。计算混和物中碳酸锂和碳酸钡的物质的量之比。
【分析】可将碳酸钙的式量理解为碳酸锂和碳酸钡的混和物的平均式量,利用十字交叉法计算可得碳酸锂和碳酸钡的物质的量之比97:26
n1 —M2
=
n2 M1—
m1 ω3—ω2
=
m2 ω1—ω3
V1 c3—c2
=
V2 c1—c3
PAGE
2
同课章节目录
