5.1 总数平均数与方差的估计-试卷

5.1总体平均数与方差的估计
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题6分）
1．从总体中抽取一部分数据作为样本去估计总体的某种属性，下面叙述正确的是（　　）
A．样本容量越大，样本平均数就越大
B．样本容量越大，样本的标准差就越大
C．样本容量越小，样本平均标准差就越大
D．样本容量越大，对总体的估计就越准确
2．为了了解某地区七年级学生每天体育锻炼的时间，要进行抽样调查．以下是几个主要步骤：①随机选择该地区一部分七年级学生完成调查问卷；②设计调查问卷；③用样本估计总体；④整理数据；⑤分析数据．正确的顺序是（　　）
A．①②④⑤③ B．②①③④⑤ C．②①④③⑤ D．②①④⑤③
3．从某地某一个月中随机抽取5天的中午，记录这5天12时的气温（单位：℃），结果如下：22 32 25 13 18
可估计该地这一个月中午12时的平均气温为（　　）℃．
A．13 B．22 C．25 D．32
4．从某校2100名学生随机抽取一个30名学生的样本，样本中每个学生用于课外作业的时间（单位：min）依次为：75，80，85，65，95，100，70，55，65，75，85，110，120，80，85，80，75，90，90，95，70，60，60，75，90，95，65，75，80，80．则该校的所有学生中，课外作业时间超过一个半小时（含一个半小时）的学生人数为（　　）
A．9 B．270 C．630 D．1050
5．某商店进行“迎五一，大促销”摸奖活动，凡是有购物小票的顾客均可摸球一次，摸到的是白球即可获奖．规则如下：一个不透明的袋子中装有10个黑球和若干白球，它们除颜色不同外，其余均相同，从袋子中随机摸出一个球，记下颜色，再把它放回袋子中摇匀，重复此过程．共有300人摸球，其中获奖的共有180人，由此估计袋子中白球个数大约为（　　）
A．10 B．12 C．15 D．16
二．填空题（共5小题，每题6分）
6．某校在一次期末考试中，随机抽取七年级30名学生的数学成绩进行分析，其中3名学生的数学成绩达108分以上．据此估计该校七年级360名学生中期末考试数学成绩达108分以上的学生约有　 　名．
7．工人师傅测量一种圆柱体工件的直径，随机抽取10件测量，得到以下数值（单位：cm）．8.03，8.04，7.95，7.98，7.95，7.98，8.00，7.98，7.94，8.05．如果要取其中一个数据作为工件直径的估计值，则该估计值是　 　cm，理由是　 　．
8．国庆节期间，小李调查了“福美小区”10户家庭一周内使用环保袋的数量，数据如下（单位：只）：6、5、7、8、7、5、8、10、5、9．据此，估计该小区2000户家庭一周内使用环保袋的数量约为　 　只．
9．某家庭搬进新居为了了解用电量的多少，该家庭在六月份连续几天观察电表的千瓦时数，电表显示的千瓦时数如下表
日期
1日
2日
3日
4日
电表显示千瓦时数
115
118
122
127
于是，可以估计这个家庭6月份的用电总量是　 　千瓦时．
10．某商场4月份抽查了6天的营业额，结果是（单位：万元）：2.8，3.2，3.4，3.7，3.0，3.1，则该商场这6天平均每天的营业额是　 　万元，估计4月份的总营业额大约是　 　万元．
三．解答题（共3小题，第11、12题各12分，第13题16分）
11．为了估计鱼塘中鱼的条数，养鱼者首先从鱼塘中打捞30条鱼做上标记，然后放归鱼塘，经过一段时间，等有标记的鱼完全混合于鱼群中，再打捞200条鱼，发现其中带标记的鱼有5条，则鱼塘中估计有多少条鱼．若第三次打捞上10条，它们的质量分别为1.8，2，2.2，1.9，2.1 2.3 1.7 2 2.6 1，4千克，请估计这塘鱼的产量．
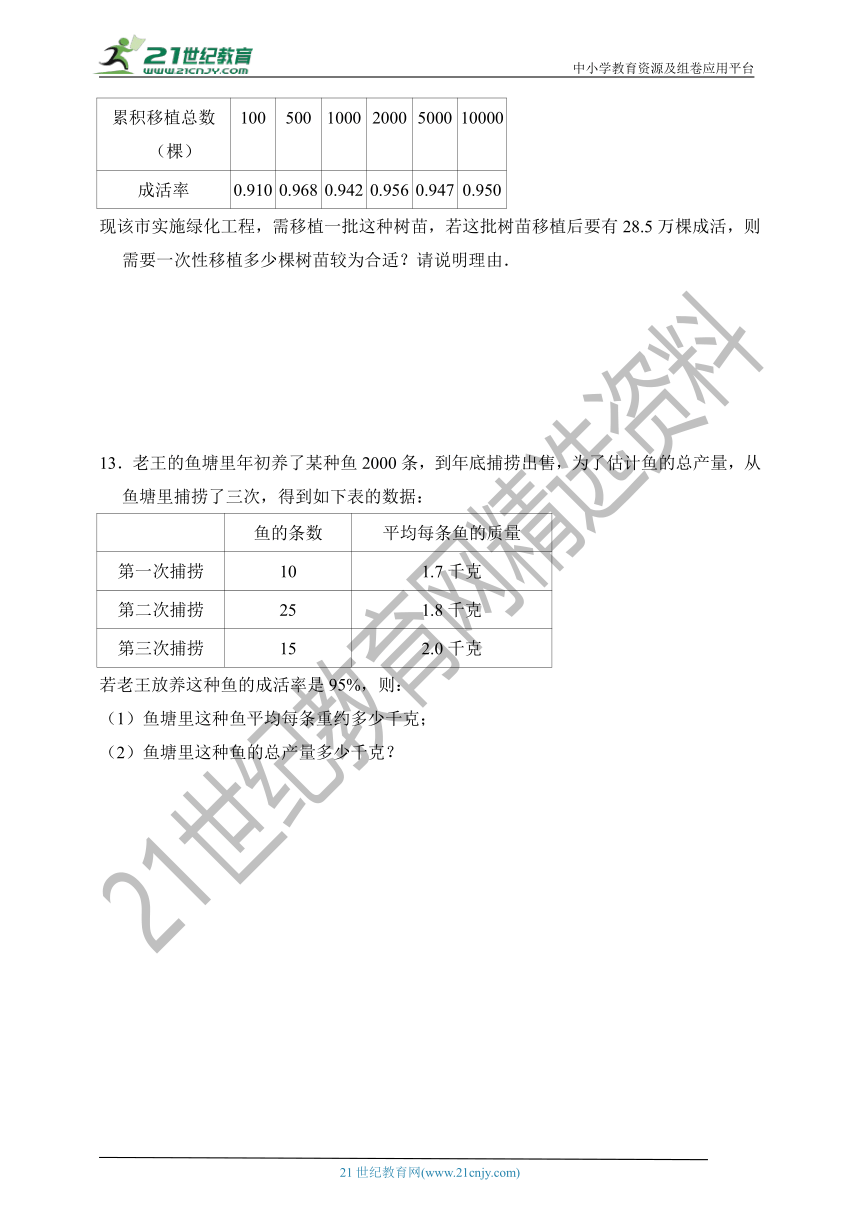
12．某市一家园林公司培育出新品种树苗，为考察这种树苗的移植的成活率，公司进行了统计，结果如图所示．
累积移植总数（棵）
100
500
1000
2000
5000
10000
成活率
0.910
0.968
0.942
0.956
0.947
0.950
现该市实施绿化工程，需移植一批这种树苗，若这批树苗移植后要有28.5万棵成活，则需要一次性移植多少棵树苗较为合适？请说明理由．
13．老王的鱼塘里年初养了某种鱼2000条，到年底捕捞出售，为了估计鱼的总产量，从鱼塘里捕捞了三次，得到如下表的数据：
鱼的条数
平均每条鱼的质量
第一次捕捞
10
1.7千克
第二次捕捞
25
1.8千克
第三次捕捞
15
2.0千克
若老王放养这种鱼的成活率是95%，则：
（1）鱼塘里这种鱼平均每条重约多少千克；
（2）鱼塘里这种鱼的总产量多少千克？

试题解析
一．选择题
1．【分析】用样本频率估计总体分布的过程中，估计的是否准确与总体的数量无关，只与样本容量在总体中所占的比例有关，对于同一个总体，样本容量越大，估计的越准确．
【解答】解：∵用样本频率估计总体分布的过程中，
估计的是否准确与总体的数量无关，
只与样本容量在总体中所占的比例有关，
∴样本容量越大，估计的越准确．
故选：D．
【点评】此题考查了抽样和样本估计总体的实际应用，注意在一个总体中抽取一定的样本估计总体，估计的是否准确，只与样本在总体中所占的比例有关．
2．【分析】直接利用调查收集数据的过程与方法分析排序即可．
【解答】解：解决一个问题所要经历的几个主要步骤为②设计调查问卷，再①随机选择该地区一部分七年级学生完成调查问卷；④整理数据；⑤分析数据；③用样本估计总体．
则正确的顺序是：②①④⑤③；
故选：D．
【点评】此题主要考查了调查收集数据的过程与方法，正确掌握调查的过程是解题关键．
3．【分析】计算出这5天12时的气温的平均数，据此即可估计该地这一个月中午12时的平均气温．
【解答】解：∵这5天12时的气温的平均数为
22+32+25+13+18
5
=22（℃），
∴可估计该地这一个月中午12时的平均气温为22℃，
故选：B．
【点评】本题主要考查样本估计总体，一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．
4．【分析】先求出样本中课外作业时间超过一个半小时（含一个半小时）的学生所占的百分比，再利用样本估计总体的思想，用2100乘以这个百分比即可．
【解答】解：∵样本中课外作业时间超过一个半小时（含一个半小时）的学生所占的百分比是：
9
30
×100%=30%，
∴该校的所有学生中，课外作业时间超过一个半小时（含一个半小时）的学生人数为：2100×30%=630．
故选：C．
【点评】本题考查了用样本估计总体，让整体×样本的百分比即可．求出样本中课外作业时间超过一个半小时（含一个半小时）的学生所占的百分比是解题的关键．
5．【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，设未知数列出方程求解．
/
【点评】本题考查利用频率估计概率．大量反复试验下频率稳定值即概率．关键是根据白球的频率得到相应的等量关系．
二．填空题
6．【分析】先求出随机抽取的30名学生中成绩达到108分以上的所占的百分比，再乘以360，即可得出答案．
【解答】解：∵随机抽取30名学生的数学成绩进行分析，有3名学生的成绩达108分以上，
∴七年级360名学生中期末考试数学成绩达108分以上的学生约有360×
3
30
=36（名）；
故答案为：36．
【点评】此题考查了用样本估计总体，用样本估计整体让整体×样本的百分比即可．
7．【分析】根据利用样本估计总体的意义得出即可．
【解答】解：该估计值是：答案不唯一，如：7.98cm，
理由是：出现频数最多．
故答案为：答案不唯一，如：7.98；出现频数最多．
【点评】此题主要考查了用样本估计总体，正确理解估计总体的方法是解题关键．
8．【分析】先求出10户家庭一周内使用环保方便袋的数量总和，然后求得样本平均数，最后乘以总数2000即可解答．
【解答】解：
1
10
（6+5+7+8+7+5+8+10+5+9）×2000=14000只．
故答案为：14000
【点评】本题考查的是通过样本去估计总体，只需将样本“成比例地放大”为总体即可．
9．【分析】先求抽查3天的平均用电量，即可认为是6月份每天的平均用电量，乘以天数30，即可求出6月份的总用电量．
【解答】解：这3天的平均用电量为
127?115
3
=4（千瓦时），
则估计这个家庭6月份的用电总量是30×4=120（千瓦时），
故答案为：120．
【点评】本题考查的是通过样本去估计总体．注意统计表中是统计的是3天的用电量及平均数的定义．
10．【分析】该商场4月份的营业额可以用上面6天的营业额来估计，即算出随机抽查的6天的营业额的平均数，然后乘以4月份30天即可解答．
【解答】解：（2.8+3.2+3.4+3.7+3.0+3.1）÷6=3.2，
3.2×30=96（万元）．
估算该商场4月份的总营业额大约是 96万元，
故答案为3.2，96．
【点评】本题考查了用样本的数据特征来估计总体的数据特征，利用样本中的数据对整体进行估算是统计学中最常用的估算方法，难度适中．
三．解答题
11．【分析】首先求出有记号的5条鱼在200条鱼中所占的比例，然后根据用样本中有记号的鱼所占的比例等于鱼塘中有记号的鱼所占的比例，即可求得鱼的总条数．求得样本中10条鱼的平均质量，再乘以鱼的总数量可得
【解答】解：设鱼塘中的鱼共有x条，
则
30
??
=
5
200
，
解得：x=1200，
经检验x=1200是原分式方程的解，
则鱼塘中估计有1200条鱼；
∵
1.8+2+2.2+1.9+2.1+2.3+1.7+2+2.6+1.4
10
=2，
∴1200×2=2400，
答：估计这塘鱼的产量约为2400千克．
【点评】本题考查的是通过样本去估计总体，掌握总体平均数约等于样本平均数是解题的关键．
12．【分析】利用表格中数据估算这种幼树移植成活率的概率即可．然后用样本概率估计总体概率即可确定答案．
【解答】解：由表格可知，随着树苗移植数量的增加，树苗移植成活率越来越稳定．
当移植总数为10000时，成活率为0.950，于是可以估计树苗移植成活率为0.950，
则该市需要购买的树苗数量约为28.5÷0.950=30万棵．
【点评】此题主要考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．
13．【分析】（1）用加权平均数计算平均重量即可；
（2）用鱼的平均重量乘以成活后的鱼的数量即可求得鱼的总重量．
【解答】解：（1）鱼的平均重量为：
10×1.7+25×1.8+15×2
10+25+15
=1.84千克．
答：鱼塘里这种鱼平均每条的质量约1.84千克；
（2）鱼的总重量为2000×95%×1.84=3496千克．
答：鱼塘里这种鱼的总质量估计是3496千克．
【点评】本题考查了用样本估计总体、加权平均数的知识，解题的关键是正确的用公式求得加权平均数，难度不大．
/