人教版数学八年级上册13.1轴对称专项练习(含答案)
文档属性
| 名称 | 人教版数学八年级上册13.1轴对称专项练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 83.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 14:53:37 | ||
图片预览

文档简介
八年级上册 13.1 轴对称 专项练习(含答案)
(满分:100分)
班级:______ 姓名:______ 学号:____ 成绩:____
一、选择题(每小题3分,共36分)
1、点M 关于x轴的对称点的坐标是
?A. B. C. D.
2、下列图形是轴对称图形的有 ( )
A、2个 B、3个 C、4个 D、5个
3、如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG = 40°,则∠GEF的度数为 ( )
A.100° B.110° ?C.120° D.135°
4、如右图所示,在RtΔACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )
A.9 ?B.8 ?C.7 ?D.6
5、如图,△ABC中,AB=AC,∠A=45o,AC的垂直平分线分别交AB、AC于D、E,若CD=1,则BD等于( )
A.1 B. C. D.
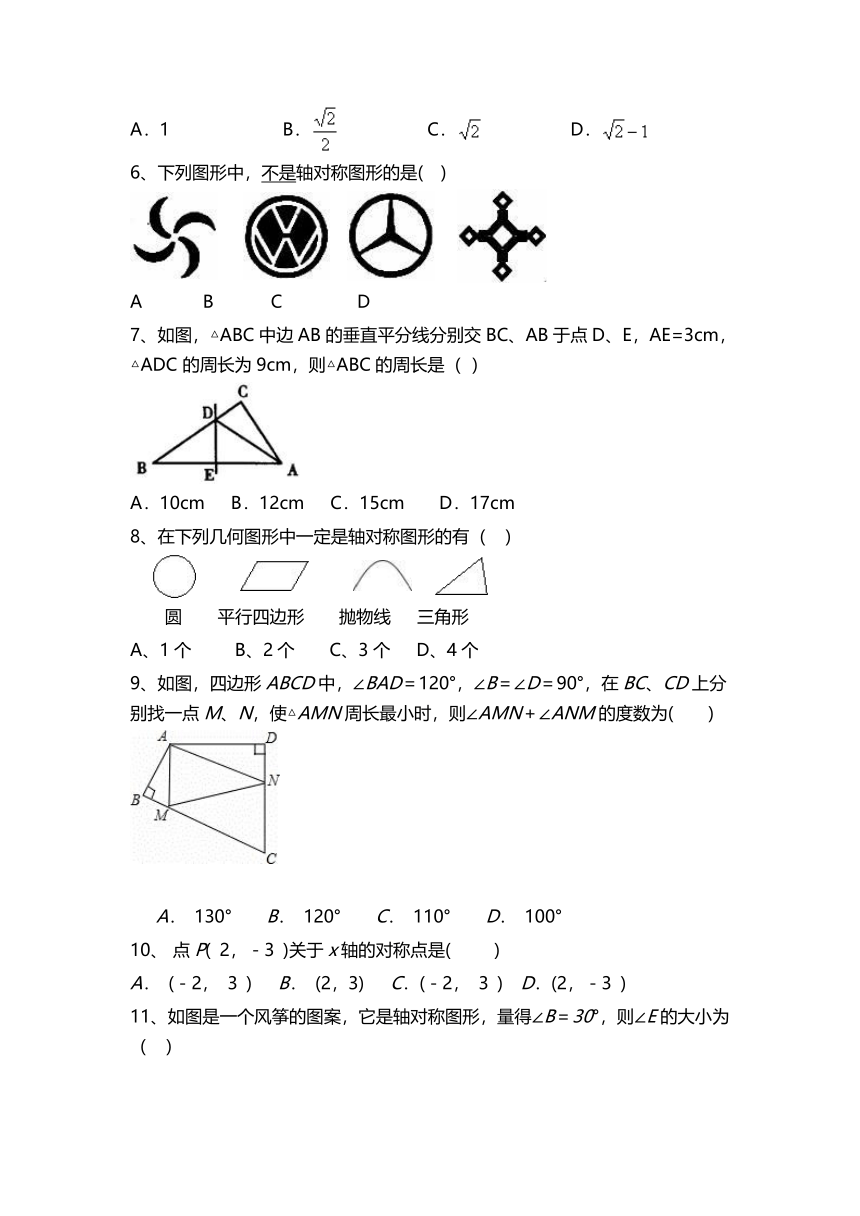
6、下列图形中,不是轴对称图形的是( )
?
A B ?C ?D
7、如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
8、在下列几何图形中一定是轴对称图形的有( ) ?
? ? ?
圆 平行四边形 抛物线 三角形
A、1个 B、2个 C、3个 D、4个
9、如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
10、?点P( 2,-3 )关于x轴的对称点是( )
A. (-2, 3 ) B. (2,3) C.(-2, 3 ) D.(2,-3 )
11、如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的大小为( )
A.30° B.35° C.40° D.45°
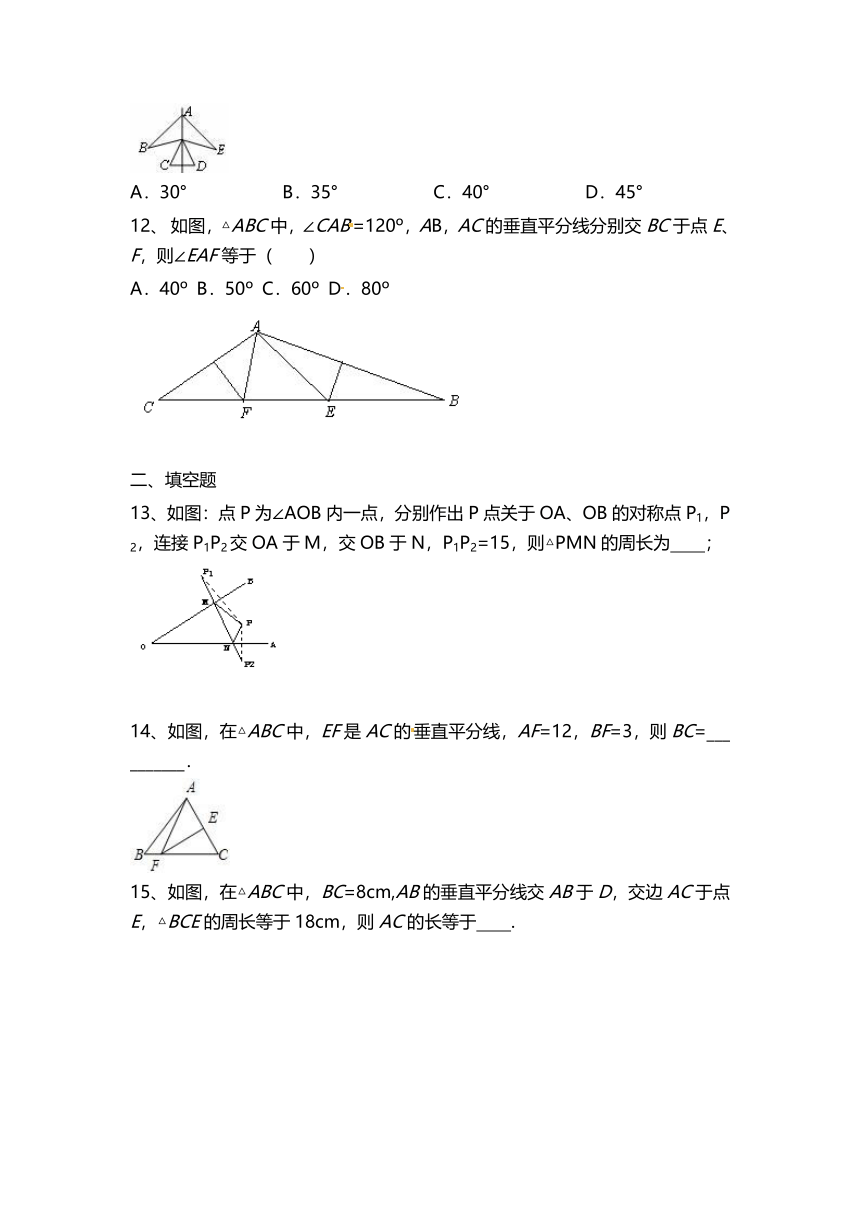
12、?如图,△ABC中,∠CAB=120o,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF等于( )
A.40o B.50o C.60o D.80o
二、填空题
13、如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 ;
14、如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
15、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 .
?
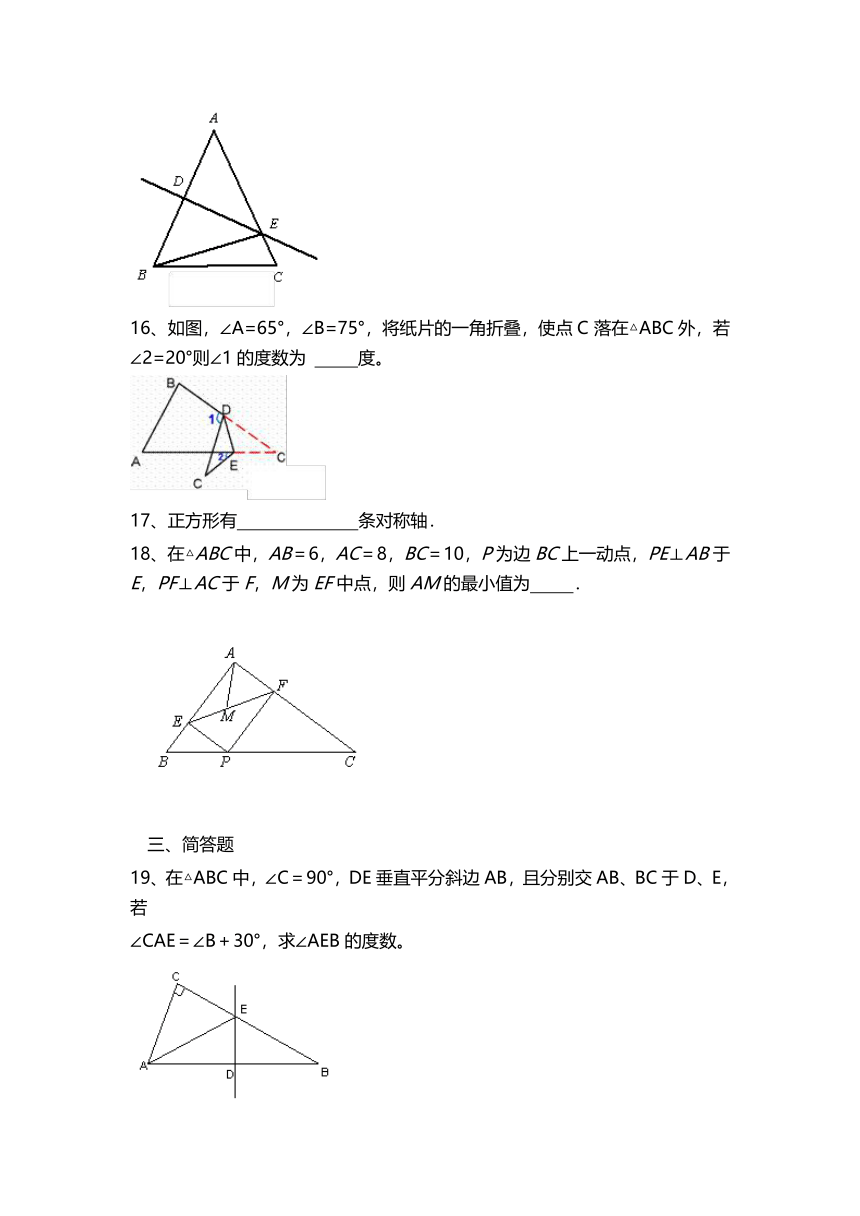
16、如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°则∠1的度数为 度。
17、正方形有 条对称轴.
18、在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
三、简答题
19、在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若
∠CAE=∠B+30°,求∠AEB的度数。
20、?如图,把两个全等的腰长为8的等腰直角三角形沿他们的斜边拼接得到四边形ABCD,N是斜边AC上一动点.
(Ⅰ)若E、F为AC的三等分点,求证:∠ADE=∠CBF;
(Ⅱ)若M是DC上一点,且DM=2,求DN+MN的最小值;
(注:计算时可使用如下定理:在直角△ABC中,若∠C=90°,则AB2=AC2+BC2.)
(Ⅲ)若点P在射线BC上,且NB=NP,求证:NP⊥ND.
参考答案
一、选择题
1、A
2、C
3、B
4、D
5、D
6、A
7、C
8、B?
9、考点:
轴对称-最短路线问题。
分析:
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
解答:
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠EAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:B.
点评:
此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
10、B
11、A
12、C.
二、填空题
13、15
14、15.
15、10cm
16、100
17、4
18、答案:2.4
三、简答题
19、解:∵DE垂直平分斜边AB,∴AE=BE,∴∠B=∠EAB。∵∠C=90°,
∴∠CAB+∠B=90°。又∵∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°。
∴∠B=20°。∴∠AEB=180°-∠EAB-∠B=180°-20°-20°=140°。
20、?(Ⅰ)证明:∵E、F为AC的三等分点,
?
∴AE=AC,CF=AC,∴AE=CF.
∵AB=BC,∠ABC=90°,
∵∠BAC=∠BCA=45°.
?同理∠DAC=45°.
?∴∠BCA=∠DAC.
∵△ASC≌△CDA,
?∴CB=AD.
∴在△ADE和△CBF中,
AE=CF,
∠DAE=∠BCF,
AD=CB,
∴△ADE≌△CBF(SAS).
∴∠ADE=∠CBF.
(Ⅱ)∵D、B关于AC对称,所以当B、N、M在一直线上时,DN+MN最小.
∵AB=8,DM=2,∴CM=6.
在Rt△MCB中,∠MCB=90°,CM=6,BC=8,根据题中定理可求出BM=10.
∴DN+MN最小值为10.
(Ⅲ)①当点P在线段BC上(P与B、C不重合)时,
∵NB=NP, ∴∠NBP=∠NPB.
∵D、B关于AC对称,
∴∠NBP=∠NDC.
∴∠NPB+∠NPC=∠NDC+∠NPC=180°.
∴∠DNP=360°-(∠BCD+∠NDC+∠NPC)=90°.
∴NP⊥ND. ②当点P与点C重合时,点N恰好在AC的中点处,
∵∠NDC=∠NCD=45°,∴∠DNC=90°.
∴NP⊥ND.
③当点P在BC延长线上时,
∵NB=NP,∴∠NBP=∠NPB.
∴D、B关于AC对称,∠NBP=∠NDC.
∴∠NPC=∠NDC.∵∠DHN=∠CHP,
∴∠DNP=∠DCP=90°.∴NP⊥ND.
?
?
?
(满分:100分)
班级:______ 姓名:______ 学号:____ 成绩:____
一、选择题(每小题3分,共36分)
1、点M 关于x轴的对称点的坐标是
?A. B. C. D.
2、下列图形是轴对称图形的有 ( )
A、2个 B、3个 C、4个 D、5个
3、如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG = 40°,则∠GEF的度数为 ( )
A.100° B.110° ?C.120° D.135°
4、如右图所示,在RtΔACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )
A.9 ?B.8 ?C.7 ?D.6
5、如图,△ABC中,AB=AC,∠A=45o,AC的垂直平分线分别交AB、AC于D、E,若CD=1,则BD等于( )
A.1 B. C. D.
6、下列图形中,不是轴对称图形的是( )
?
A B ?C ?D
7、如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
8、在下列几何图形中一定是轴对称图形的有( ) ?
? ? ?
圆 平行四边形 抛物线 三角形
A、1个 B、2个 C、3个 D、4个
9、如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
10、?点P( 2,-3 )关于x轴的对称点是( )
A. (-2, 3 ) B. (2,3) C.(-2, 3 ) D.(2,-3 )
11、如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的大小为( )
A.30° B.35° C.40° D.45°
12、?如图,△ABC中,∠CAB=120o,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF等于( )
A.40o B.50o C.60o D.80o
二、填空题
13、如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 ;
14、如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
15、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 .
?
16、如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°则∠1的度数为 度。
17、正方形有 条对称轴.
18、在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
三、简答题
19、在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若
∠CAE=∠B+30°,求∠AEB的度数。
20、?如图,把两个全等的腰长为8的等腰直角三角形沿他们的斜边拼接得到四边形ABCD,N是斜边AC上一动点.
(Ⅰ)若E、F为AC的三等分点,求证:∠ADE=∠CBF;
(Ⅱ)若M是DC上一点,且DM=2,求DN+MN的最小值;
(注:计算时可使用如下定理:在直角△ABC中,若∠C=90°,则AB2=AC2+BC2.)
(Ⅲ)若点P在射线BC上,且NB=NP,求证:NP⊥ND.
参考答案
一、选择题
1、A
2、C
3、B
4、D
5、D
6、A
7、C
8、B?
9、考点:
轴对称-最短路线问题。
分析:
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
解答:
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠EAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:B.
点评:
此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
10、B
11、A
12、C.
二、填空题
13、15
14、15.
15、10cm
16、100
17、4
18、答案:2.4
三、简答题
19、解:∵DE垂直平分斜边AB,∴AE=BE,∴∠B=∠EAB。∵∠C=90°,
∴∠CAB+∠B=90°。又∵∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°。
∴∠B=20°。∴∠AEB=180°-∠EAB-∠B=180°-20°-20°=140°。
20、?(Ⅰ)证明:∵E、F为AC的三等分点,
?
∴AE=AC,CF=AC,∴AE=CF.
∵AB=BC,∠ABC=90°,
∵∠BAC=∠BCA=45°.
?同理∠DAC=45°.
?∴∠BCA=∠DAC.
∵△ASC≌△CDA,
?∴CB=AD.
∴在△ADE和△CBF中,
AE=CF,
∠DAE=∠BCF,
AD=CB,
∴△ADE≌△CBF(SAS).
∴∠ADE=∠CBF.
(Ⅱ)∵D、B关于AC对称,所以当B、N、M在一直线上时,DN+MN最小.
∵AB=8,DM=2,∴CM=6.
在Rt△MCB中,∠MCB=90°,CM=6,BC=8,根据题中定理可求出BM=10.
∴DN+MN最小值为10.
(Ⅲ)①当点P在线段BC上(P与B、C不重合)时,
∵NB=NP, ∴∠NBP=∠NPB.
∵D、B关于AC对称,
∴∠NBP=∠NDC.
∴∠NPB+∠NPC=∠NDC+∠NPC=180°.
∴∠DNP=360°-(∠BCD+∠NDC+∠NPC)=90°.
∴NP⊥ND. ②当点P与点C重合时,点N恰好在AC的中点处,
∵∠NDC=∠NCD=45°,∴∠DNC=90°.
∴NP⊥ND.
③当点P在BC延长线上时,
∵NB=NP,∴∠NBP=∠NPB.
∴D、B关于AC对称,∠NBP=∠NDC.
∴∠NPC=∠NDC.∵∠DHN=∠CHP,
∴∠DNP=∠DCP=90°.∴NP⊥ND.
?
?
?
