人教版数学八年级上册13.2画轴对称图形同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级上册13.2画轴对称图形同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 77.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 14:56:34 | ||
图片预览


文档简介
八年级上册 13.2 画轴对称图形 专项练习(含答案)
(满分:100分)
班级:______ 姓名:______ 学号:____ 成绩:____
一、选择题(每小题3分,共36分)
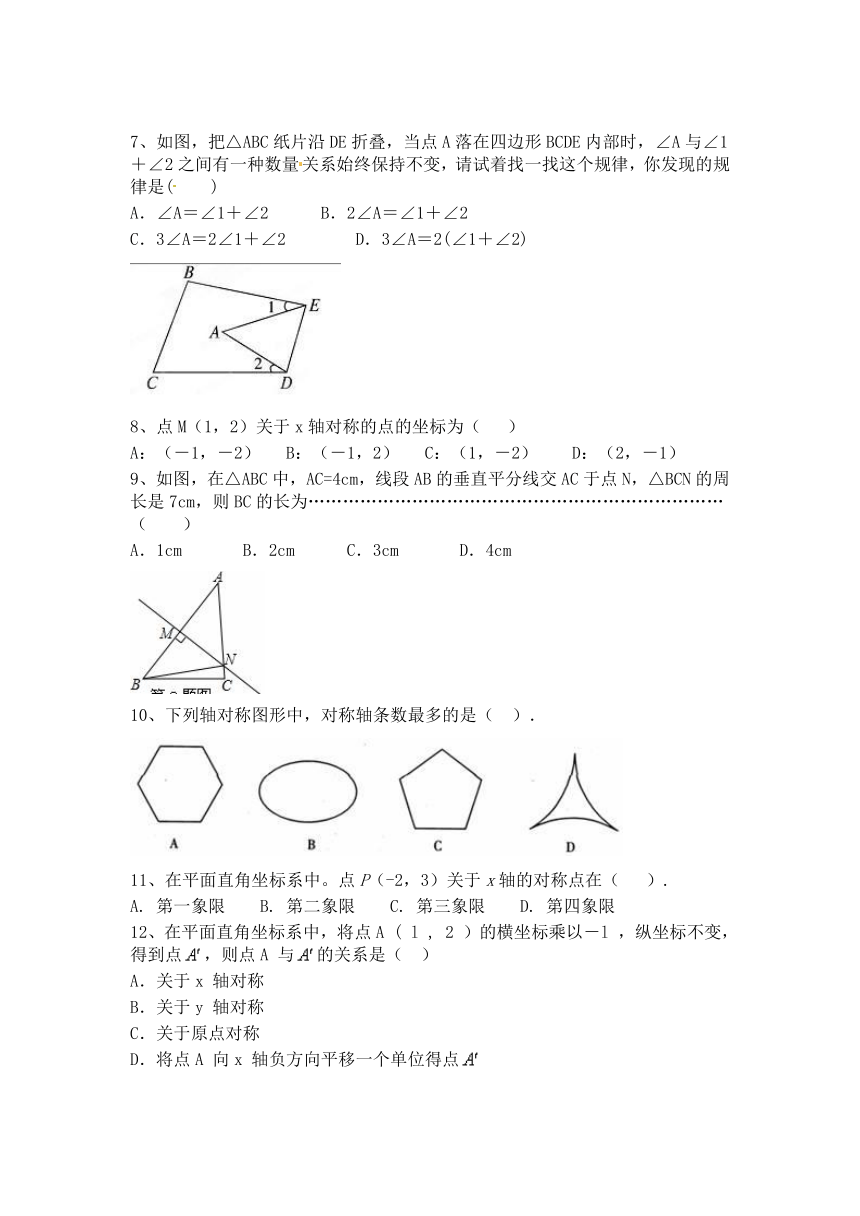
1、这是映在水中的一辆汽车的牌号倒影,如图,你能说出这辆汽车的牌号吗?( ?)
A.P90753 B.b90753 C.P60723 D.P90723
2、已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2005的值为( ).
A.0 B.-1 C.1 D.(-3)2005
3、小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是 ( )
4、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. B. 4 C. D. 5
5、在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
6、下列图案中,有且只有三条对称轴的是(????) ?
A. A?? B. B? ??C. C? ???D. D?????????????
7、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
8、点M(1,2)关于x轴对称的点的坐标为( )
A:(-1,-2) ?B:(-1,2) C:(1,-2) ?D:(2,-1)
9、如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为………………………………………………………………( )
A.1cm B.2cm C.3cm D.4cm
10、下列轴对称图形中,对称轴条数最多的是( ).
11、在平面直角坐标系中。点P(-2,3)关于x轴的对称点在( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
12、在平面直角坐标系中,将点A ( l , 2 )的横坐标乘以-l ,纵坐标不变,得到点,则点A 与的关系是( )
A.关于x 轴对称
B.关于y 轴对称
C.关于原点对称
D.将点A 向x 轴负方向平移一个单位得点
二、填空题
13、如图,E是正方形ABCD边AD上一点,AE=2cm,DE=6cm,P是对角线BD上的一动点,则AP+PE的最小值是 .
?
14、若点P1(–1,3)和P2(1,b)关于y轴对称,则b= .
15、如图,ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=___________.
16、若,求P(-a,b)关于y轴的对轴点P′的坐标。
17、如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若CD=18cm,则△PMN的周长为________.
18、点E(a,-5)与点F(-2,b)关于y轴对称,则a= ,b= ;
三、简答题
19、探究:
(1)如图①,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2= ;
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣ = ,猜想∠BDA+∠CEA与∠A的关系为 .
20、已知:如图所示,A、B两村庄在一条小河的同一侧,要在河边建一自来水厂向A、B两村庄供水。
(1)在a图中,若要使厂址到A、B两村的距离相等,厂址应设在哪个位置?
(2)在b图中若要使厂址到A、B两村的水管最省料,厂址应设在哪个位置?
a图 b图
参考答案
一、选择题
1、D
2、B 解:∵P1(a-1,5)和P2(2,b-1)关于x轴对称.
∴ ∴a=3,b=-4.
∴(a+b)2005=(3-4)2005=-1.
3、D
4、C
5、B
6、D
7、B
8、C
9、C;
10、A
11、C;
12、B
二、填空题
13、10cm
14、?3
15、10cm
16、(2/3,3)
17、18cm
18、2,-5
三、简答题
19、考点:
翻折变换(折叠问题).
专题:
探究型.
分析:
根据三角形内角是180度可得出,∠1+∠2=∠B+∠C,从而求出当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°,有以上计算可归纳出一般规律:∠BDA+∠CEA=2∠A.
解答:
解:(1)根据三角形内角是180°可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;(3)如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣300°=60°,
所以∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
点评:
本题考查图形的翻折变换和三角形,四边形内角和定理,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
20、(1)在a图中,若要使厂址到A、B两村的距离相等,厂址应设在哪个位置?
作线段AB的垂直平分线
(2)在b图中若要使厂址到A、B两村的水管最省料,厂址应设在哪个位置?
作点A关于直线l的对称点A’,连结A’B 与l交点即为所求。
(作点B关于直线l的对称点亦可)
(满分:100分)
班级:______ 姓名:______ 学号:____ 成绩:____
一、选择题(每小题3分,共36分)
1、这是映在水中的一辆汽车的牌号倒影,如图,你能说出这辆汽车的牌号吗?( ?)
A.P90753 B.b90753 C.P60723 D.P90723
2、已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2005的值为( ).
A.0 B.-1 C.1 D.(-3)2005
3、小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是 ( )
4、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. B. 4 C. D. 5
5、在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
6、下列图案中,有且只有三条对称轴的是(????) ?
A. A?? B. B? ??C. C? ???D. D?????????????
7、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
8、点M(1,2)关于x轴对称的点的坐标为( )
A:(-1,-2) ?B:(-1,2) C:(1,-2) ?D:(2,-1)
9、如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为………………………………………………………………( )
A.1cm B.2cm C.3cm D.4cm
10、下列轴对称图形中,对称轴条数最多的是( ).
11、在平面直角坐标系中。点P(-2,3)关于x轴的对称点在( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
12、在平面直角坐标系中,将点A ( l , 2 )的横坐标乘以-l ,纵坐标不变,得到点,则点A 与的关系是( )
A.关于x 轴对称
B.关于y 轴对称
C.关于原点对称
D.将点A 向x 轴负方向平移一个单位得点
二、填空题
13、如图,E是正方形ABCD边AD上一点,AE=2cm,DE=6cm,P是对角线BD上的一动点,则AP+PE的最小值是 .
?
14、若点P1(–1,3)和P2(1,b)关于y轴对称,则b= .
15、如图,ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=___________.
16、若,求P(-a,b)关于y轴的对轴点P′的坐标。
17、如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若CD=18cm,则△PMN的周长为________.
18、点E(a,-5)与点F(-2,b)关于y轴对称,则a= ,b= ;
三、简答题
19、探究:
(1)如图①,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2= ;
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣ = ,猜想∠BDA+∠CEA与∠A的关系为 .
20、已知:如图所示,A、B两村庄在一条小河的同一侧,要在河边建一自来水厂向A、B两村庄供水。
(1)在a图中,若要使厂址到A、B两村的距离相等,厂址应设在哪个位置?
(2)在b图中若要使厂址到A、B两村的水管最省料,厂址应设在哪个位置?
a图 b图
参考答案
一、选择题
1、D
2、B 解:∵P1(a-1,5)和P2(2,b-1)关于x轴对称.
∴ ∴a=3,b=-4.
∴(a+b)2005=(3-4)2005=-1.
3、D
4、C
5、B
6、D
7、B
8、C
9、C;
10、A
11、C;
12、B
二、填空题
13、10cm
14、?3
15、10cm
16、(2/3,3)
17、18cm
18、2,-5
三、简答题
19、考点:
翻折变换(折叠问题).
专题:
探究型.
分析:
根据三角形内角是180度可得出,∠1+∠2=∠B+∠C,从而求出当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°,有以上计算可归纳出一般规律:∠BDA+∠CEA=2∠A.
解答:
解:(1)根据三角形内角是180°可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;(3)如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣300°=60°,
所以∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
点评:
本题考查图形的翻折变换和三角形,四边形内角和定理,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
20、(1)在a图中,若要使厂址到A、B两村的距离相等,厂址应设在哪个位置?
作线段AB的垂直平分线
(2)在b图中若要使厂址到A、B两村的水管最省料,厂址应设在哪个位置?
作点A关于直线l的对称点A’,连结A’B 与l交点即为所求。
(作点B关于直线l的对称点亦可)
