人教版九年级上24.1.2垂直于弦的直径同步练习(含答案解析)
文档属性
| 名称 | 人教版九年级上24.1.2垂直于弦的直径同步练习(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 14:59:22 | ||
图片预览


文档简介
2018-2019学年度人教版数学九年级上册同步练习
24.1.2 垂直于弦的直径
一.选择题(共15小题)
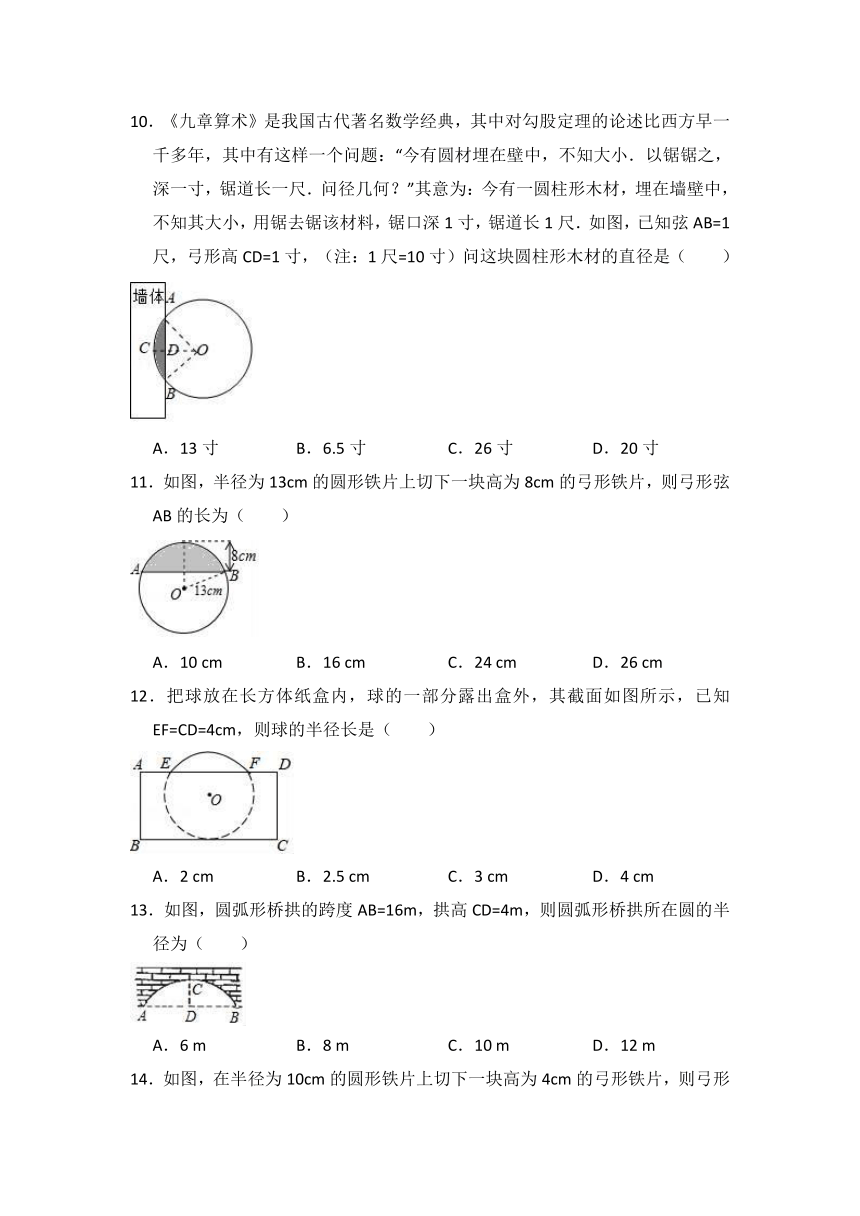
1.下列说法中正确的是( )
A.平分弦的直径一定垂直于弦
B.长度相等的弧是等弧
C.平行弦所夹的两条弧相等
D.相等的圆心角所对的弦相等
2.如图,⊙O的半径为6,直径CD过弦EF的中点G,若∠EOD=60°,则弦CF的长等于( )
A.6 B.6 C.3 D.9
3.如图,在⊙O中,直径AB⊥弦CD,垂足为M,则下列结论一定正确的是( )
A.AC=CD B.OM=BM C.∠A=∠ACD D.∠A=∠BOD
4.如图,AB是⊙O的直径,AB⊥CD于E,AB=10,CD=8,则BE为( )
A.2 B.3 C.4 D.3.5
5.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6cm,则⊙O的半径是( )
A.6cm B.10cm C.8cm D.20cm
6.在半径为25cm的⊙O中,弦AB=40cm,则弦AB所对的弧的中点到AB的距离是( )
A.10cm B.15cm C.40cm D.10cm或40cm
7.下列说法中正确的个数有( )
①相等的圆心角所对的弧相等;
②平分弦的直径一定垂直于弦;
③圆是轴对称图形,每一条直径都是对称轴;
④直径是弦;
⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
8.如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
A. B.5 C. D.6
9.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
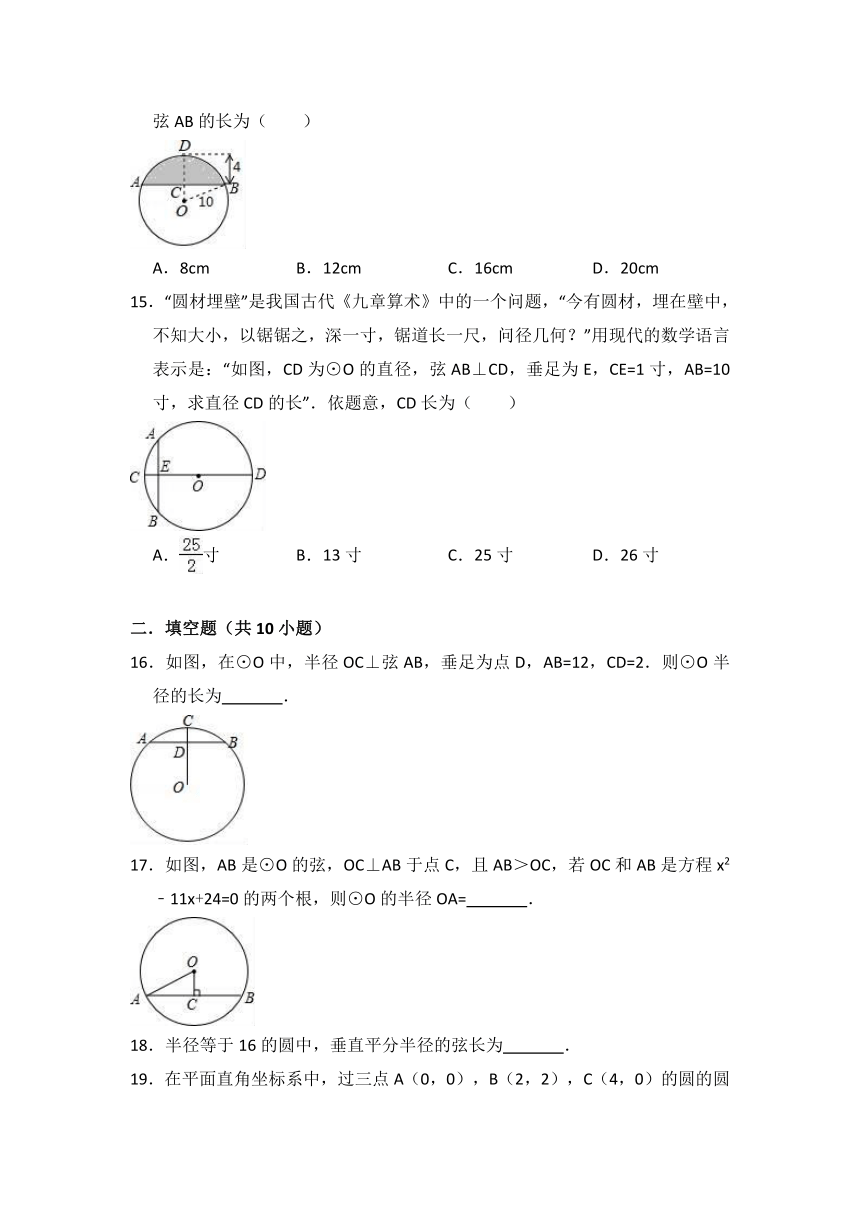
10.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
A.13寸 B.6.5寸 C.26寸 D.20寸
11.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10 cm B.16 cm C.24 cm D.26 cm
12.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
13.如图,圆弧形桥拱的跨度AB=16m,拱高CD=4m,则圆弧形桥拱所在圆的半径为( )
A.6 m B.8 m C.10 m D.12 m
14.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为( )
A.8cm B.12cm C.16cm D.20cm
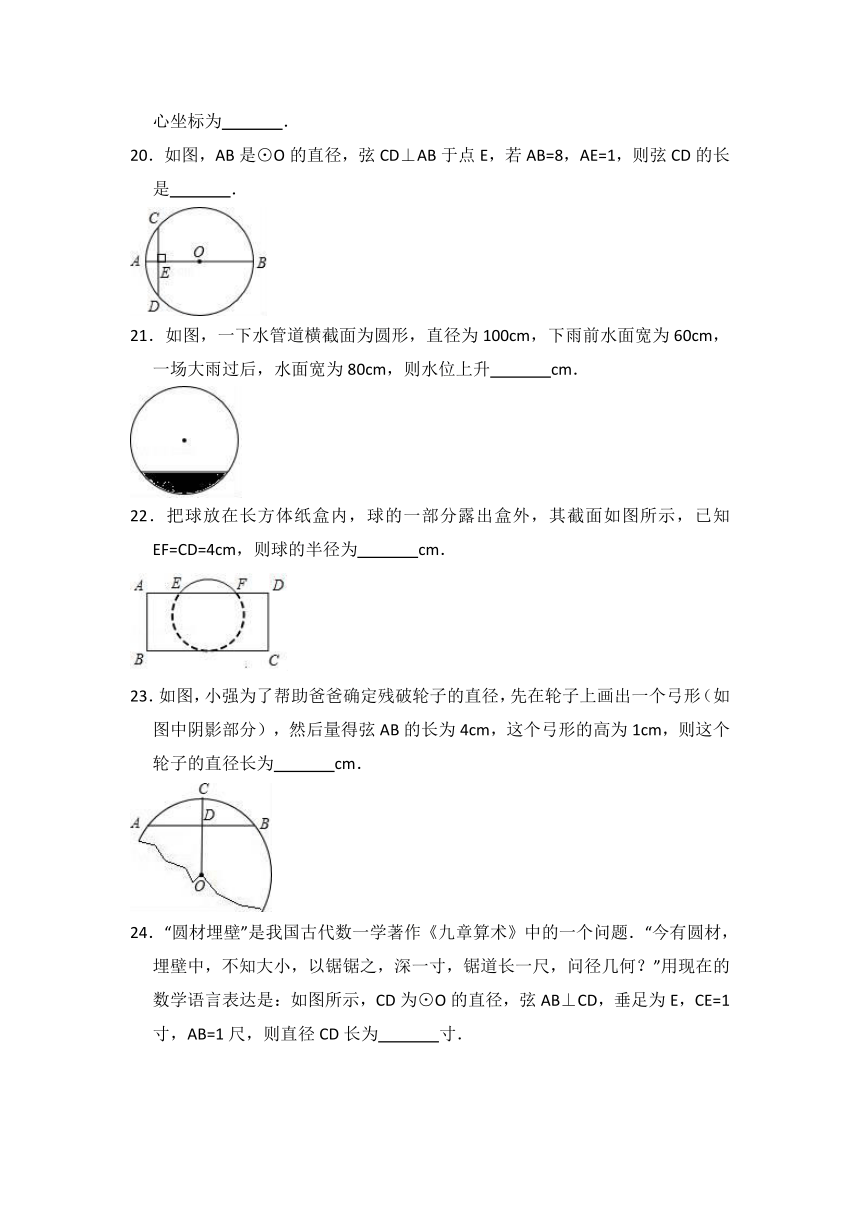
15.“圆材埋壁”是我国古代《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的数学语言表示是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.依题意,CD长为( )
A.寸 B.13寸 C.25寸 D.26寸
二.填空题(共10小题)
16.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=12,CD=2.则⊙O半径的长为 .
17.如图,AB是⊙O的弦,OC⊥AB于点C,且AB>OC,若OC和AB是方程x2﹣11x+24=0的两个根,则⊙O的半径OA= .
18.半径等于16的圆中,垂直平分半径的弦长为 .
19.在平面直角坐标系中,过三点A(0,0),B(2,2),C(4,0)的圆的圆心坐标为 .
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是 .
21.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
22.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
23.如图,小强为了帮助爸爸确定残破轮子的直径,先在轮子上画出一个弓形(如图中阴影部分),然后量得弦AB的长为4cm,这个弓形的高为1cm,则这个轮子的直径长为 cm.
24.“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为 寸.
25.如图,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m,现准备打掉部分墙体,使其变成以AC为直径的圆弧形门,则打掉墙体后,弧形门洞的周长(含线段BC)为 .
三.解答题(共6小题)
26.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
27.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
28.已知:如图,⊙O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,求AC的长.
29.一条排水管的截面如图所示,已知排水管的半径OA=10m,水面宽AB=12m,某天下雨后,水管水面上升了2m,求此时排水管水面的宽CD.
30.某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
31.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
参考答案与试题解析
一.选择题(共15小题)
1.【解答】解:A、当两条弦都是直径时不成立,故本选项错误;
B、在同圆或等圆中,两个长度相等的弧是等弧,故本选项错误;
C、如图所示,两弦平行,则圆周角相等,圆周角相等,则弧相等;故本选项正确;
D、在同圆或等圆中,相等的圆心角所对的弧相等,故本选项错误.
故选:C.
2.【解答】解:连接DF,
∵直径CD过弦EF的中点G,
∴=,
∴∠DCF=∠EOD=30°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴CF=CD?cos∠DCF=12×=6,
故选:B.
3.【解答】解:连接DA,
∵直径AB⊥弦CD,垂足为M,
∴CM=MD,∠CAB=∠DAB,
∵2∠DAB=∠BOD,
∴∠CAD=∠BOD,
故选:D.
4.【解答】解:连接OC.
∵AB是⊙O的直径,AB=10,
∴OC=OB=AB=5;
又∵AB⊥CD于E,CD=8,
∴CE=CD=4(垂径定理);
在Rt△COE中,OE=3(勾股定理),
∴BE=OB﹣OE=5﹣3=2,即BE=2;
故选:A.
5.【解答】解:过点O作OE⊥AB于点E,连接OC,
∵弦AB的长为16cm,圆心O到AB的距离为6cm
∴OE=6cm,AE=AB=8cm,
在Rt△AOE中,根据勾股定理得,OA==10cm
故选:B.
6.【解答】解:点C和D为弦AB所对弧的中点,连结CD交AB于E,连结OA,如图,
∵点C和D为弦AB所对弧的中点,
∴CD为直径,CD⊥AB,
∴AE=BE=AB=20,
在Rt△OAE中,∵OA=25,AE=20,
∴OE==15,
∴DE=OD+OE=40,CE=OC﹣OE=10,
即弦AB和弦AB所对的劣弧的中点的距离为10cm,弦AB和弦AB所对的优弧的中点的距离为40cm.
故选:D.
7.【解答】解:①相等的圆心角所对的弧相等;错误.必须在同圆或等圆中;
②平分弦的直径一定垂直于弦;错误,此弦不是直径;
③圆是轴对称图形,每一条直径都是对称轴;错误,应该是每一条直径所在的直线都是对称轴;
④直径是弦;正确;
⑤长度相等的弧是等弧.错误.能够完全重合的两条弧是等弧;
故选:A.
8.【解答】解:延长AO交BC于点D,连接OB,由对称性及等腰Rt△ABC,得到AD⊥BC,
∴D为BC的中点,即BD=CD=BC=4,AD=BC=4,
∵OA=2,∴OD=AD﹣OA=4﹣2=2,
在Rt△BOD中,根据勾股定理得:OB==2,
则圆的半径为2.
故选:C.
9.【解答】解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
10.【解答】解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
11.【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
12.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
13.【解答】解:如图,设OA=r,则OD=r﹣4,
∵AB=16m,
∴AD=8m.
在Rt△AOD中,
∵OD2+AD2=OA2,即(r﹣4)2+82=r2,解得r=10(m).
故选:C.
14.【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=4,OD=10,
∴OC=6,
又∵OB=10,
∴Rt△BCO中,BC=,
∴AB=2BC=16.
故选:C.
15.【解答】解:连接OA.设圆的半径是x尺,在直角△OAE中,OA=x,OE=x﹣1,
∵OA2=OE2+AE2,
则x2=(x﹣1)2+25,
解得:x=13.
则CD=2×13=26(cm).
故选:D.
二.填空题(共10小题)
16.【解答】解:连接AO,
∵半径OC⊥弦AB,
∴AD=BD,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴OD=R﹣2,
在Rt△AOD中,OA2=OD2+AD2,即:R2=(R﹣2)2+62,
∴R=10,
答:⊙O的半径长为10.
17.【解答】解:x2﹣11x+24=0
(x﹣3)(x﹣8)=0
x﹣3=0,x﹣8=0,
x1=3,x2=8,
∵AB>OC,
∴AB=8,OC=3,
∵OC⊥AB,
∴AC=AB=4,
由勾股定理得,OA==5,
故答案为:5.
18.【解答】解:如图,OA=16,则OC=8,
根据勾股定理得,AC==8,
∴弦AB=16.
故答案为:16.
19.【解答】解:已知A(0,0),B(2,2),C(4,0),如图:
可设:AB的垂直平分线解析式为:y=kx+b,把(0,2),(2,0)代入解析式可得:,
解得:,
所以AB的垂直平分线解析式是y=﹣x+2,
设AC的垂直平分线解析式为x=m,把(2,2)代入解析式,可得:x=2,
所以AC的垂直平分线解析式是x=2,
∴过A、B、C三点的圆的圆心坐标为(2,0).
故答案为:(2,0).
20.【解答】解:连接OC,
由题意,得
OE=OA﹣AE=4﹣1=3,
CE=ED==,
CD=2CE=2,
故答案为2.
21.【解答】解:作半径OD⊥AB于C,连接OB
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下时 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
22.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
23.【解答】解:连接OB;
Rt△OBD中,BD=AB=2cm,
根据勾股定理得:
OD2+BD2=OB2,即:
(OB﹣1)2+22=OB2,
解得:OB=2.5;
所以轮子的直径为5cm.
故答案为:5.
24.【解答】解:连接OA,设OA=r,则OE=r﹣CE=r﹣1,
∵AB⊥CD,AB=1尺,
∴AE=AB=5寸,
在Rt△OAE中,
OA2=AE2+OE2,即r2=52+(r﹣1)2,
解得r=13(寸).
∴CD=2r=26寸.
故答案为:26.
25.【解答】解:设矩形外接圆的圆心为O,连接OB,
∵矩形ABCD的AC=2m,BC=1m,
∴OB=OC=BC=1m,
∴△OBC是等边三角形,
∴∠BOC=60°.
∴弧形门洞的周长(含线段BC)为: +1=+1,
故答案为:(+1)m.
三.解答题(共6小题)
26.【解答】解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
27.【解答】解:连结BE,如图,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,
解得 x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
28.【解答】解:连接BC,
∵AB是直径,
CF=FD=4,
∴AB⊥CD,
∵∠ACB=90°
∴∠A=∠BCF,
∴△BCF∽△CAF,
∴=,
∴CF2=AF?BF,
设AF=x,
∴16=2x,
∴x=8,
∴由勾股定理可知:AC=4
29.【解答】解:如图:作OE⊥AB于E,交CD于F,
∵AB=12m,OE⊥AB,OA=1m,
∴OE=8m.
∵水管水面上升了2m,
∴OF=8﹣2=6m,
∴CF==8m,
∴CD=16m.
30.【解答】解:过点O作OC⊥AB于D,交⊙O于C,连接OB,
∵OC⊥AB
∴BD=AB=×16=8cm
由题意可知,CD=4cm
∴设半径为xcm,则OD=(x﹣4)cm
在Rt△BOD中,
由勾股定理得:OD2+BD2=OB2
(x﹣4)2+82=x2
解得:x=10.
答:这个圆形截面的半径为10cm.
31.【解答】解:(1)连结OA,
由题意得:AD=AB=30,OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34;
(2)连结OA′,
∵OE=OP﹣PE=30,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16.
∴A′B′=32.
∵A′B′=32>30,
∴不需要采取紧急措施.
24.1.2 垂直于弦的直径
一.选择题(共15小题)
1.下列说法中正确的是( )
A.平分弦的直径一定垂直于弦
B.长度相等的弧是等弧
C.平行弦所夹的两条弧相等
D.相等的圆心角所对的弦相等
2.如图,⊙O的半径为6,直径CD过弦EF的中点G,若∠EOD=60°,则弦CF的长等于( )
A.6 B.6 C.3 D.9
3.如图,在⊙O中,直径AB⊥弦CD,垂足为M,则下列结论一定正确的是( )
A.AC=CD B.OM=BM C.∠A=∠ACD D.∠A=∠BOD
4.如图,AB是⊙O的直径,AB⊥CD于E,AB=10,CD=8,则BE为( )
A.2 B.3 C.4 D.3.5
5.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6cm,则⊙O的半径是( )
A.6cm B.10cm C.8cm D.20cm
6.在半径为25cm的⊙O中,弦AB=40cm,则弦AB所对的弧的中点到AB的距离是( )
A.10cm B.15cm C.40cm D.10cm或40cm
7.下列说法中正确的个数有( )
①相等的圆心角所对的弧相等;
②平分弦的直径一定垂直于弦;
③圆是轴对称图形,每一条直径都是对称轴;
④直径是弦;
⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
8.如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
A. B.5 C. D.6
9.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
10.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
A.13寸 B.6.5寸 C.26寸 D.20寸
11.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10 cm B.16 cm C.24 cm D.26 cm
12.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
13.如图,圆弧形桥拱的跨度AB=16m,拱高CD=4m,则圆弧形桥拱所在圆的半径为( )
A.6 m B.8 m C.10 m D.12 m
14.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为( )
A.8cm B.12cm C.16cm D.20cm
15.“圆材埋壁”是我国古代《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的数学语言表示是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.依题意,CD长为( )
A.寸 B.13寸 C.25寸 D.26寸
二.填空题(共10小题)
16.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=12,CD=2.则⊙O半径的长为 .
17.如图,AB是⊙O的弦,OC⊥AB于点C,且AB>OC,若OC和AB是方程x2﹣11x+24=0的两个根,则⊙O的半径OA= .
18.半径等于16的圆中,垂直平分半径的弦长为 .
19.在平面直角坐标系中,过三点A(0,0),B(2,2),C(4,0)的圆的圆心坐标为 .
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是 .
21.如图,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水面宽为80cm,则水位上升 cm.
22.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
23.如图,小强为了帮助爸爸确定残破轮子的直径,先在轮子上画出一个弓形(如图中阴影部分),然后量得弦AB的长为4cm,这个弓形的高为1cm,则这个轮子的直径长为 cm.
24.“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为 寸.
25.如图,花园边墙上有一宽为1m的矩形门ABCD,量得门框对角线AC的长为2m,现准备打掉部分墙体,使其变成以AC为直径的圆弧形门,则打掉墙体后,弧形门洞的周长(含线段BC)为 .
三.解答题(共6小题)
26.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
27.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
28.已知:如图,⊙O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,求AC的长.
29.一条排水管的截面如图所示,已知排水管的半径OA=10m,水面宽AB=12m,某天下雨后,水管水面上升了2m,求此时排水管水面的宽CD.
30.某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
31.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
参考答案与试题解析
一.选择题(共15小题)
1.【解答】解:A、当两条弦都是直径时不成立,故本选项错误;
B、在同圆或等圆中,两个长度相等的弧是等弧,故本选项错误;
C、如图所示,两弦平行,则圆周角相等,圆周角相等,则弧相等;故本选项正确;
D、在同圆或等圆中,相等的圆心角所对的弧相等,故本选项错误.
故选:C.
2.【解答】解:连接DF,
∵直径CD过弦EF的中点G,
∴=,
∴∠DCF=∠EOD=30°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴CF=CD?cos∠DCF=12×=6,
故选:B.
3.【解答】解:连接DA,
∵直径AB⊥弦CD,垂足为M,
∴CM=MD,∠CAB=∠DAB,
∵2∠DAB=∠BOD,
∴∠CAD=∠BOD,
故选:D.
4.【解答】解:连接OC.
∵AB是⊙O的直径,AB=10,
∴OC=OB=AB=5;
又∵AB⊥CD于E,CD=8,
∴CE=CD=4(垂径定理);
在Rt△COE中,OE=3(勾股定理),
∴BE=OB﹣OE=5﹣3=2,即BE=2;
故选:A.
5.【解答】解:过点O作OE⊥AB于点E,连接OC,
∵弦AB的长为16cm,圆心O到AB的距离为6cm
∴OE=6cm,AE=AB=8cm,
在Rt△AOE中,根据勾股定理得,OA==10cm
故选:B.
6.【解答】解:点C和D为弦AB所对弧的中点,连结CD交AB于E,连结OA,如图,
∵点C和D为弦AB所对弧的中点,
∴CD为直径,CD⊥AB,
∴AE=BE=AB=20,
在Rt△OAE中,∵OA=25,AE=20,
∴OE==15,
∴DE=OD+OE=40,CE=OC﹣OE=10,
即弦AB和弦AB所对的劣弧的中点的距离为10cm,弦AB和弦AB所对的优弧的中点的距离为40cm.
故选:D.
7.【解答】解:①相等的圆心角所对的弧相等;错误.必须在同圆或等圆中;
②平分弦的直径一定垂直于弦;错误,此弦不是直径;
③圆是轴对称图形,每一条直径都是对称轴;错误,应该是每一条直径所在的直线都是对称轴;
④直径是弦;正确;
⑤长度相等的弧是等弧.错误.能够完全重合的两条弧是等弧;
故选:A.
8.【解答】解:延长AO交BC于点D,连接OB,由对称性及等腰Rt△ABC,得到AD⊥BC,
∴D为BC的中点,即BD=CD=BC=4,AD=BC=4,
∵OA=2,∴OD=AD﹣OA=4﹣2=2,
在Rt△BOD中,根据勾股定理得:OB==2,
则圆的半径为2.
故选:C.
9.【解答】解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
10.【解答】解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
11.【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
12.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
13.【解答】解:如图,设OA=r,则OD=r﹣4,
∵AB=16m,
∴AD=8m.
在Rt△AOD中,
∵OD2+AD2=OA2,即(r﹣4)2+82=r2,解得r=10(m).
故选:C.
14.【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=4,OD=10,
∴OC=6,
又∵OB=10,
∴Rt△BCO中,BC=,
∴AB=2BC=16.
故选:C.
15.【解答】解:连接OA.设圆的半径是x尺,在直角△OAE中,OA=x,OE=x﹣1,
∵OA2=OE2+AE2,
则x2=(x﹣1)2+25,
解得:x=13.
则CD=2×13=26(cm).
故选:D.
二.填空题(共10小题)
16.【解答】解:连接AO,
∵半径OC⊥弦AB,
∴AD=BD,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴OD=R﹣2,
在Rt△AOD中,OA2=OD2+AD2,即:R2=(R﹣2)2+62,
∴R=10,
答:⊙O的半径长为10.
17.【解答】解:x2﹣11x+24=0
(x﹣3)(x﹣8)=0
x﹣3=0,x﹣8=0,
x1=3,x2=8,
∵AB>OC,
∴AB=8,OC=3,
∵OC⊥AB,
∴AC=AB=4,
由勾股定理得,OA==5,
故答案为:5.
18.【解答】解:如图,OA=16,则OC=8,
根据勾股定理得,AC==8,
∴弦AB=16.
故答案为:16.
19.【解答】解:已知A(0,0),B(2,2),C(4,0),如图:
可设:AB的垂直平分线解析式为:y=kx+b,把(0,2),(2,0)代入解析式可得:,
解得:,
所以AB的垂直平分线解析式是y=﹣x+2,
设AC的垂直平分线解析式为x=m,把(2,2)代入解析式,可得:x=2,
所以AC的垂直平分线解析式是x=2,
∴过A、B、C三点的圆的圆心坐标为(2,0).
故答案为:(2,0).
20.【解答】解:连接OC,
由题意,得
OE=OA﹣AE=4﹣1=3,
CE=ED==,
CD=2CE=2,
故答案为2.
21.【解答】解:作半径OD⊥AB于C,连接OB
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下时 水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
故答案为10或70.
22.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
23.【解答】解:连接OB;
Rt△OBD中,BD=AB=2cm,
根据勾股定理得:
OD2+BD2=OB2,即:
(OB﹣1)2+22=OB2,
解得:OB=2.5;
所以轮子的直径为5cm.
故答案为:5.
24.【解答】解:连接OA,设OA=r,则OE=r﹣CE=r﹣1,
∵AB⊥CD,AB=1尺,
∴AE=AB=5寸,
在Rt△OAE中,
OA2=AE2+OE2,即r2=52+(r﹣1)2,
解得r=13(寸).
∴CD=2r=26寸.
故答案为:26.
25.【解答】解:设矩形外接圆的圆心为O,连接OB,
∵矩形ABCD的AC=2m,BC=1m,
∴OB=OC=BC=1m,
∴△OBC是等边三角形,
∴∠BOC=60°.
∴弧形门洞的周长(含线段BC)为: +1=+1,
故答案为:(+1)m.
三.解答题(共6小题)
26.【解答】解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
27.【解答】解:连结BE,如图,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,
解得 x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
28.【解答】解:连接BC,
∵AB是直径,
CF=FD=4,
∴AB⊥CD,
∵∠ACB=90°
∴∠A=∠BCF,
∴△BCF∽△CAF,
∴=,
∴CF2=AF?BF,
设AF=x,
∴16=2x,
∴x=8,
∴由勾股定理可知:AC=4
29.【解答】解:如图:作OE⊥AB于E,交CD于F,
∵AB=12m,OE⊥AB,OA=1m,
∴OE=8m.
∵水管水面上升了2m,
∴OF=8﹣2=6m,
∴CF==8m,
∴CD=16m.
30.【解答】解:过点O作OC⊥AB于D,交⊙O于C,连接OB,
∵OC⊥AB
∴BD=AB=×16=8cm
由题意可知,CD=4cm
∴设半径为xcm,则OD=(x﹣4)cm
在Rt△BOD中,
由勾股定理得:OD2+BD2=OB2
(x﹣4)2+82=x2
解得:x=10.
答:这个圆形截面的半径为10cm.
31.【解答】解:(1)连结OA,
由题意得:AD=AB=30,OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34;
(2)连结OA′,
∵OE=OP﹣PE=30,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16.
∴A′B′=32.
∵A′B′=32>30,
∴不需要采取紧急措施.
同课章节目录
