山西省平顺艺校函数奇偶性( 11张}
文档属性
| 名称 | 山西省平顺艺校函数奇偶性( 11张} |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-02 17:54:14 | ||
图片预览




文档简介
函数的基本性质
平顺艺校
2018.10.18
函数奇偶性
目录
01
函数奇偶性的定义
02
函数奇偶性的运算性质
03
复合函数的奇偶性
04
用定义法判断函数奇偶性
01
函数奇偶性的定义
偶函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x), 那么函数f(x)就叫偶函数.
奇函数定义:
如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x) ,那么函数f(x)就叫奇函数.
01
函数奇偶性的定义
对奇函数、偶函数定义的说明:
定义域关于原点对称是函数具有奇偶性的必要条件(前提条件)
01
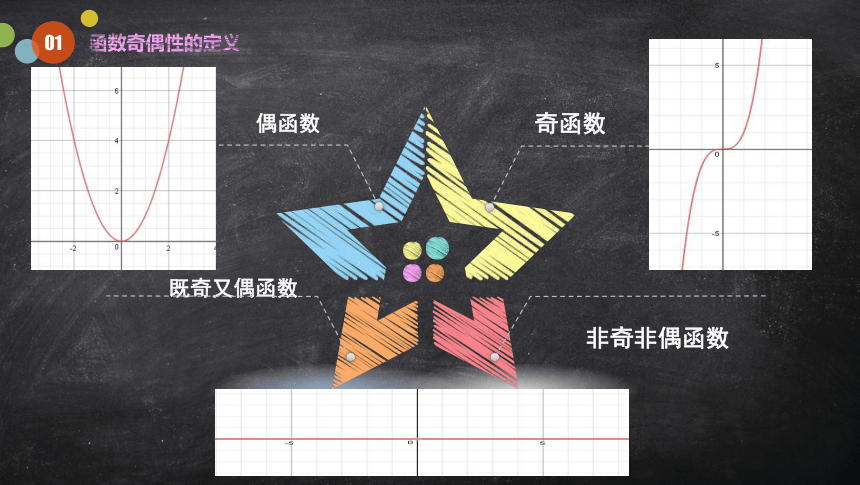
函数奇偶性的定义
奇函数
偶函数
非奇非偶函数
既奇又偶函数
02
函数奇偶性的运算性质
02
函数奇偶性的运算性质
函数奇偶性的运算性质
常见的奇函数:x1,x3,x5,x7
常见的偶函数:x0,x2,x4,x6
奇函数+奇函数=奇函数
偶函数+偶函数=偶函数
奇函数*奇函数=偶函数,偶函数*偶函数=偶函数
奇函数*偶函数=奇函数
03
复合函数的奇偶性
03
复合函数的奇偶性f(g(x))
01
Application
02
Application
03
Application
04
Application
f(g(x))
偶函数
f(x)为偶函数
g(x)为偶函数
f(g(x))
偶函数
f(x)为偶函数
g(x)为奇函数
f(g(x))
偶函数
f(x)为奇函数
g(x)为偶函数
f(g(x))
奇函数
f(x)为奇函数
g(x)为奇函数
04
用定义法判断函数奇偶性
01
利用定义判断函数奇偶性的格式步骤
01
首先确定函数的定义域,并判断其定义域是否关于原点对称
02
确定f(-x)与f(x)的关系
如果f(-x)=-f(x)
非奇非偶函数
非奇非偶函数
偶函数
如果f(-x)=f(x)
奇函数
如果f(-x)与f(x)无任何关系
