山西平顺艺校指数函数（17张）

平顺艺校
指数函数



01
02
03
目 录
指数函数的概念
指数函数的图象及性质
指数函数底数变化与图像分布规律

指数函数的概念
01
形式上的严格性：只有形如y=ax(a>0且a≠1)的函数才是指数函数．
函数y=ax(a>0且a≠1)叫做指数函数，其中x是自变量，a为常数，函数定义域为R.
指数函数的概念
指数函数的概念

指数函数的图象及性质
02
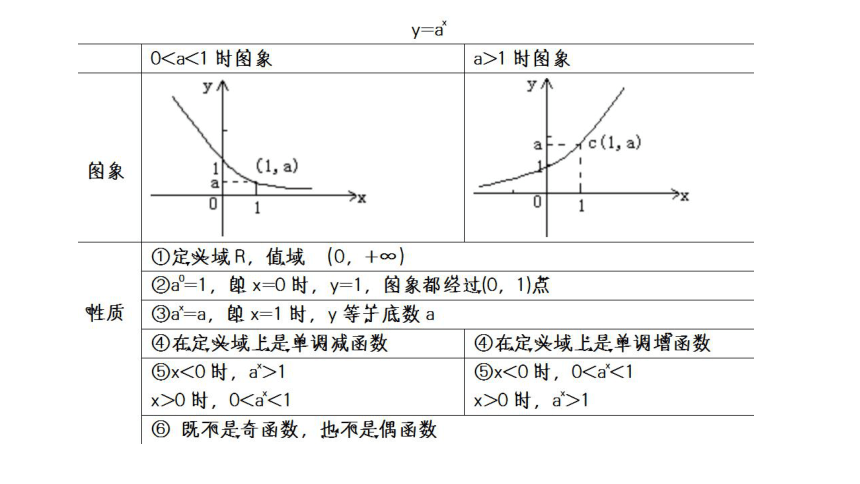
图象特征 函数性质




(1)图象都位于x轴上方
(1)x取任何实数都有ax>0
(2)图象都过（0,1 )点
(2)a为任何正数,总有a0 =1
(4)自左向右看,y=ax(a>1)的图像逐渐上升;y=ax(0(4) a>1,y=ax是增函数
当0(3)y=ax(a>1)的图像在第一 象限内的纵坐标都大于1,在第二象限的纵坐标都小于1;y=ax(0指数函数的图象及性质

指数函数底数变化与图像分布规律

03
指数函数y=ax(a>0,a≠1)中,底数a对函数图像有什么影响?
当a>1时,a的值越大,图像越靠近y轴,递增速度越快.
当0指数函数底数变化与图像分布规律
描点画出图像
(1)当x<0时,总有2x大于3x;
(2)当x>0时,总有2x小于3x;
(3)当x>0时,y=3x比y=2x的函
数值增长得快.
例3 已知函数
作出函数图像，求定义域、值域。

解：
定义域：R
值域：
0(1)当x<0时,总有ax>bx>1;
(2)当x=0时,总有ax=bx=1;
(3)当x>0时,总有0(4)指数函数的底数越大,当x>0时,其函数值减少得就越快.
指数函数底数变化与图像分布规律
a>b>1时,
(1)当x<0时,总有0(2)当x=0时,总有ax=bx=1;
(3)当x>0时,总有ax>bx>1;
(4)指数函数的底数越大,当x>0时,其函数值增长得就越快.
指数函数底数变化与图像分布规律
函 数 y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|

对于有些复合函数的图象，则常用基本函数图象+变换方法作出：即把我们熟知的基本函数图象，通过平移、作其对称图等方法，得到我们所要求作的复合函数的图象，这种方法我们遇到的有以下几种形式：

a>0时向左平移a个单位；a<0时向右平移|a|个单位.
a>0时向上平移a个单位；a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
与y=f(x)的图象关于直线y=x对称.
谢谢
平顺艺校