23.2.2 中心对称图形课件(共27张PPT)
文档属性
| 名称 | 23.2.2 中心对称图形课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 00:00:00 | ||
图片预览




文档简介
课件27张PPT。中心对称图形一.知识回顾
1.中心对称的定义:把一个图形绕着某一点旋转1800,
如果它能与另一个图形重合,那么就说这两个图形关于
这个点对称或中心对称。这个点叫做对称中心。
2. 中心对称的性质:
1、中心对称的两个图形,对称点所连线段都
经过对称中心,而且被对称中心所平分。
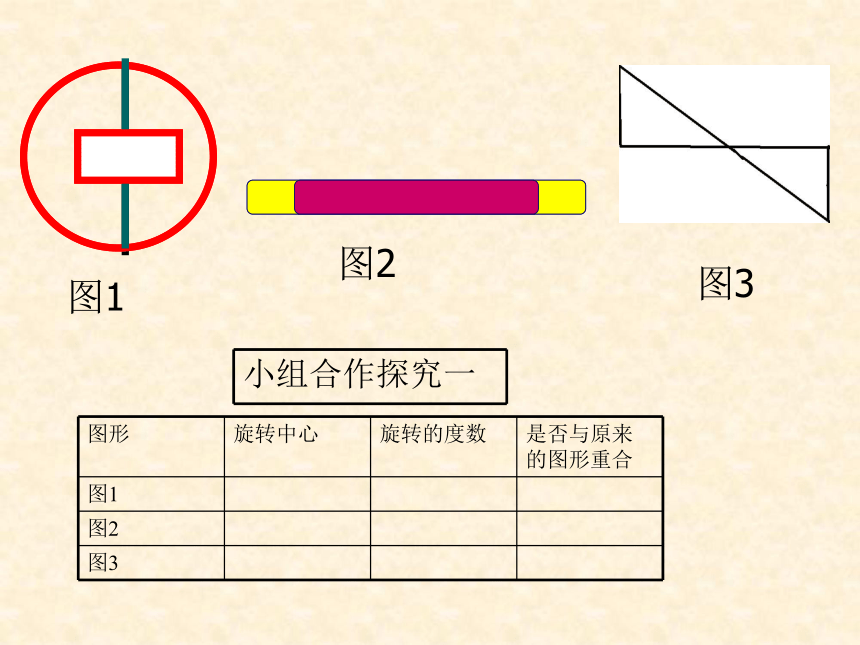
2、中心对称的两个图形是全等图形。图1图2图3
ABCDO像这样,把一个图形绕某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形。
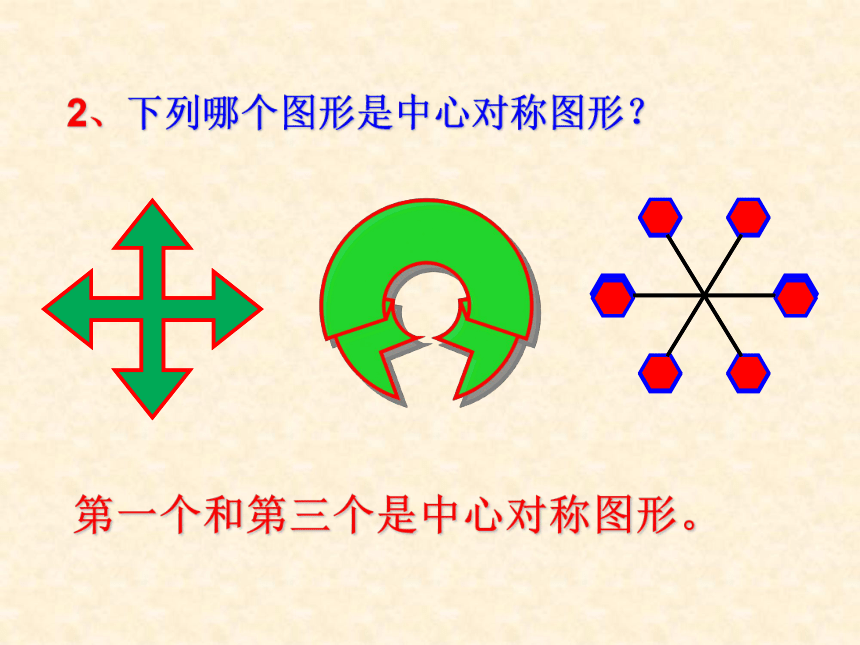
这个点就是它的对称中心。2、下列哪个图形是中心对称图形?第一个和第三个是中心对称图形。 中心对称与中心对称图形是两个既有联系又有 区别的概念 区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称联系: (1)如果将中心对称的两个图形看成一个整体,则它们是中心对称图形 (2)如果将中心对称图形,把对称的部分看
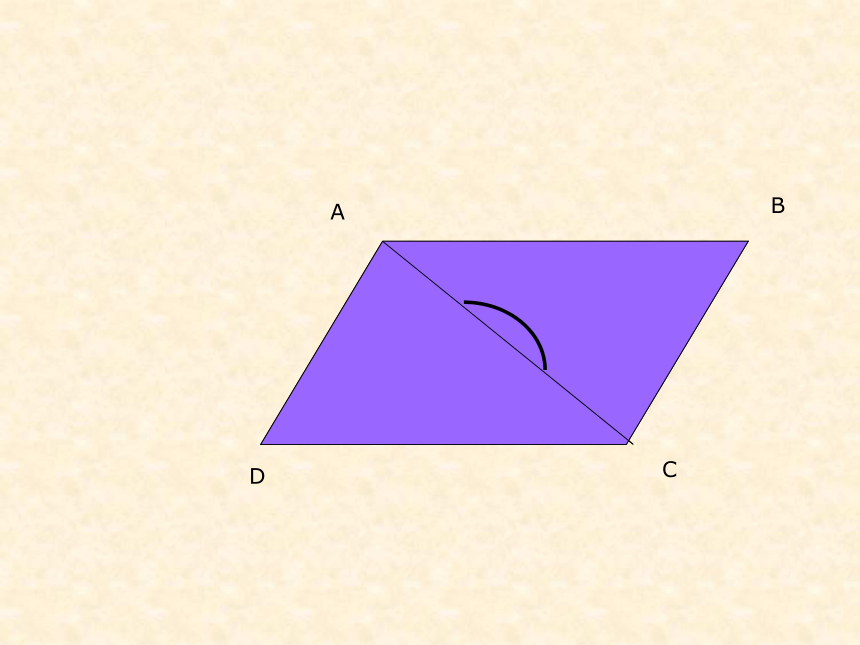
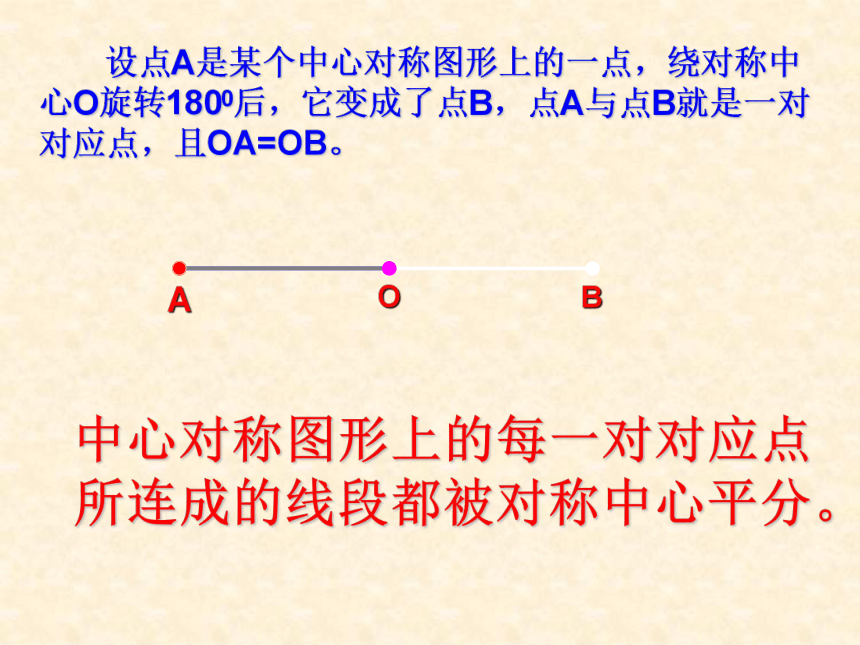
成两个图形,则它们是中心对称。 设点A是某个中心对称图形上的一点,绕对称中心O旋转1800后,它变成了点B,点A与点B就是一对对应点,且OA=OB。ABO中心对称图形上的每一对对应点所连成的线段都被对称中心平分。如图是一个中心对称图形: ⑴找出对称中心; ⑵找出P的对应点。解:O是对称中心;P’是P的对应点A作出△ABC关于点O的中心对称图形BCO如图,△ A ′B ′C ′就是所求 做一做(1)平行四边形是中心对称图形吗?如果是,请找出它的对称中心,并设法验证你的结论。
(2)根据上面的过程,你能验证平行四边形的哪些性质?(1)平行四边形是中心对称图形,对称中心是两条对角线的交点。(2)能验证平行四边形的对边相等、对角相等、对角线互相平分等性质。2、正三角形是中心对称图形吗?正五边形 呢?正六边形呢?……边数为偶数的正多边形都是中心对称图形。正七边形正八边形……√⑴是轴对称图形的有 ;在纸上写下前13个大写的英文字母,观察它们:⑵是中心对称图形的有 ;⑶既是中心对称图形,又是轴对称图形的有 ;A B C D E H I K MH I NH IA B C D E F G H I J K M N议一议(1)举出生活中的一些中心对称图形。
(2)下面的扑克牌中,哪些牌面是中心对称图形?小明先拿出图(1)所示的四张纸牌,然后背着大家将其中某一张旋转了180°,得到图(2)。问小明肯定旋转了哪一张?⑴⑵1.如果一个图形沿着一条直线折叠,直线两旁的部分能够完全 ,那么这个图形叫做轴对称图形。这条对称轴就是它的 。
2.线段是 图形,它有 条对称轴。
3.角是轴对称图形,它的对称轴是 所在的直线。
4.属于轴对称图形的是 。
(1)三角形 (2)等腰三角形
(3)锐角 (4) 矩形
5、旋转的性质你知道吗?轴对称的性质你知道吗?对比学习重合对称轴轴对称1角平分线(2) (3) (4)对称中心 ——点对称轴 ——直线图形绕中心旋转180°图形沿轴翻折180°旋转后和原来的图形重合翻折后直线两旁的部分重合一个图形一个图形轴对称图形与中心对称图形的比较 轴对称图形与中心对称图形的比较 轴对称图形与中心对称图形的比较 1、按要求画一个图形,所画图形中同时要有一个
正方形和一个圆,并且这个图形即是轴对称图形
又是中心对称图形.三、自我检测:
1 选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形C(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形A(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3B(3)在平行四边形、矩形、菱形、
正方形、梯形、等腰梯形中,哪些
图形是具有轴对称性?哪些图形是
中心对称图形?如图,有一组数排列成方阵,试计算这组数的和。这是一种对称思想的应用.本节课学到了哪些知识? (1)中心对称图形的定义. (2)中心对称图形的性质 (3)常见的中心对称图形:
(线段、圆、平行四边形、矩形、菱形、正方形、边数为偶数的正多边形等.) (4)中心对称图形的应用。知识小结结束寄语!心有多大,舞台就有多大!
放飞你的思想,发挥你的想象!
把知识融于生活,让生活充满亮丽之色!
1.中心对称的定义:把一个图形绕着某一点旋转1800,
如果它能与另一个图形重合,那么就说这两个图形关于
这个点对称或中心对称。这个点叫做对称中心。
2. 中心对称的性质:
1、中心对称的两个图形,对称点所连线段都
经过对称中心,而且被对称中心所平分。
2、中心对称的两个图形是全等图形。图1图2图3
ABCDO像这样,把一个图形绕某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形。
这个点就是它的对称中心。2、下列哪个图形是中心对称图形?第一个和第三个是中心对称图形。 中心对称与中心对称图形是两个既有联系又有 区别的概念 区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称联系: (1)如果将中心对称的两个图形看成一个整体,则它们是中心对称图形 (2)如果将中心对称图形,把对称的部分看
成两个图形,则它们是中心对称。 设点A是某个中心对称图形上的一点,绕对称中心O旋转1800后,它变成了点B,点A与点B就是一对对应点,且OA=OB。ABO中心对称图形上的每一对对应点所连成的线段都被对称中心平分。如图是一个中心对称图形: ⑴找出对称中心; ⑵找出P的对应点。解:O是对称中心;P’是P的对应点A作出△ABC关于点O的中心对称图形BCO如图,△ A ′B ′C ′就是所求 做一做(1)平行四边形是中心对称图形吗?如果是,请找出它的对称中心,并设法验证你的结论。
(2)根据上面的过程,你能验证平行四边形的哪些性质?(1)平行四边形是中心对称图形,对称中心是两条对角线的交点。(2)能验证平行四边形的对边相等、对角相等、对角线互相平分等性质。2、正三角形是中心对称图形吗?正五边形 呢?正六边形呢?……边数为偶数的正多边形都是中心对称图形。正七边形正八边形……√⑴是轴对称图形的有 ;在纸上写下前13个大写的英文字母,观察它们:⑵是中心对称图形的有 ;⑶既是中心对称图形,又是轴对称图形的有 ;A B C D E H I K MH I NH IA B C D E F G H I J K M N议一议(1)举出生活中的一些中心对称图形。
(2)下面的扑克牌中,哪些牌面是中心对称图形?小明先拿出图(1)所示的四张纸牌,然后背着大家将其中某一张旋转了180°,得到图(2)。问小明肯定旋转了哪一张?⑴⑵1.如果一个图形沿着一条直线折叠,直线两旁的部分能够完全 ,那么这个图形叫做轴对称图形。这条对称轴就是它的 。
2.线段是 图形,它有 条对称轴。
3.角是轴对称图形,它的对称轴是 所在的直线。
4.属于轴对称图形的是 。
(1)三角形 (2)等腰三角形
(3)锐角 (4) 矩形
5、旋转的性质你知道吗?轴对称的性质你知道吗?对比学习重合对称轴轴对称1角平分线(2) (3) (4)对称中心 ——点对称轴 ——直线图形绕中心旋转180°图形沿轴翻折180°旋转后和原来的图形重合翻折后直线两旁的部分重合一个图形一个图形轴对称图形与中心对称图形的比较 轴对称图形与中心对称图形的比较 轴对称图形与中心对称图形的比较 1、按要求画一个图形,所画图形中同时要有一个
正方形和一个圆,并且这个图形即是轴对称图形
又是中心对称图形.三、自我检测:
1 选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形C(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形A(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3B(3)在平行四边形、矩形、菱形、
正方形、梯形、等腰梯形中,哪些
图形是具有轴对称性?哪些图形是
中心对称图形?如图,有一组数排列成方阵,试计算这组数的和。这是一种对称思想的应用.本节课学到了哪些知识? (1)中心对称图形的定义. (2)中心对称图形的性质 (3)常见的中心对称图形:
(线段、圆、平行四边形、矩形、菱形、正方形、边数为偶数的正多边形等.) (4)中心对称图形的应用。知识小结结束寄语!心有多大,舞台就有多大!
放飞你的思想,发挥你的想象!
把知识融于生活,让生活充满亮丽之色!
同课章节目录
