2017-2018学年度第二学期北师大版九年级数学下册 第三章 圆 单元检测试卷(含答案)
文档属性
| 名称 | 2017-2018学年度第二学期北师大版九年级数学下册 第三章 圆 单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 195.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 19:45:41 | ||
图片预览

文档简介
2017-2018学年度第二学期北师大版九年级数学下册
第三章 圆 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.一只蚂蚁以每分钟厘米的速度在地面上爬行,如果它在分钟内爬行了一周,那么它爬过的最大面积约是( )平方厘米.
A. B. C. D.
?2.已知在等腰三角形中,,底边,若以顶点为圆心,以为半径作,则与
A.相交 B.相切 C.相离 D.不能确定
?3.下列说法正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线只有一条
C.圆的切线垂直于圆的半径 D.每个三角形都有一个内切圆
?4.如图,已知是的直径,是弦,,过圆心作交弧于点,连接,则的度数为( )度.
A. B. C. D.
?5.已知是的内接三角形,为直径,,,平分角于,为的内心,则的长度为( )
A. B. C. D.
?6.如图,,是的切线,切点分别为,,点在上,且是优弧,则等于( )
A. B.
C. D.
?7.下列结论正确的是( )
A.垂直于弦的弦是直径 B.圆心角等于圆周角的倍
C.平分弦的直径垂直该弦 D.圆内接四边形的对角互补
?8.如图内接于,,是的两条切线,已知,,则的弧度数为( )
A. B. C. D.
?9.如图,一块含有角的直角三角板,在水平桌面上绕点接顺时针方向旋转到的位置.若,那么顶点从开始到结束所经过的路径长为( )
A. B. C. D.
?10.如图,点在的直径延长线上,与相切,切点为,点在上,连接、,已知.下列结论:
与相切;四边形是菱形;;.
其中,正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.若正六边形的边长为,则正六边形的半径为________;周长为________;边心距为________.
?12.如图,四边形是的内接四边形,是的延长线,若,则________.
?13.某校计划在校园内修建一座周长为的花坛,同学们设计出正三角形,正方形和圆三种图案,通过计算说明使花坛面积最大的图案是________(填图形).?
14.如图,中,,,.若以为圆心,为半径的弧交斜边与点,则弧的长为________.
?15.在中,,,,是中线,以为圆心,以长为半径画圆,则点与的位置关系是________.
?16.如图,,,是上三点,当平分时,能得出结论:________(任写一个).
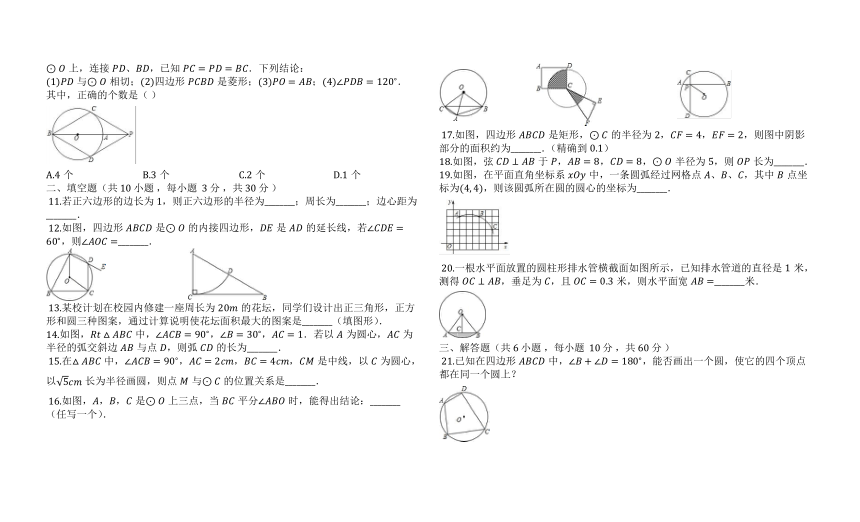
?17.如图,四边形是矩形,的半径为,,,则图中阴影部分的面积约为________.(精确到)
18.如图,弦于,,,半径为,则长为________.
19.如图,在平面直角坐标系中,一条圆弧经过网格点、、,其中点坐标为,则该圆弧所在圆的圆心的坐标为________.
?20.一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是米,测得,垂足为,且米,则水平面宽________米.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.已知在四边形中,,能否画出一个圆,使它的四个顶点都在同一个圆上?
?
22.如图,是半径为的外一点,,是的切线,为切点,弦,连接,求阴影部分的面积.
?
23.已知:,在同侧,且.求证:和有公共外接圆.
?
24.足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲,乙两名运动员分别在,两处,他们争论不休,都说在自己所在的位置对球门的张角大,如果你是教练,请评一评他们两个人谁的位置对球门的张角大?为什么?
?
25.如图,点、、都在半径为的上,过点作交的延长线于点,连接,已知.
求证:是的切线;
求图中阴影部分的面积.
?
26.如图①已知是直径,是上一点(与、不重合),,垂足为,直线交于点,过点作的切线交直线于点,试证明:是等腰三角形;26.
对第题,当点在的延长线上时,其他条件不变;如图②,中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
答案
1.A
2.B
3.D
4.A
5.B
6.C
7.D
8.A
9.D
10.A
11.
12.
13.圆
14.
15.在上
16.
17.
18.
19.
20.
21.解:能画出一个圆,使它的四个顶点都在同一个圆上.
的外接圆为,假设点不在上(在外或内),如图,当点在外,交于,连接,
因为,而,所以,同样当点在内时也得到这与圆内接四边形的性质相矛盾,所以假设错误,所以点在上,即在四边形中,,能画出一个圆,使它的四个顶点都在同一个圆上.
22.解:连接,,
∵是圆的切线,
∴,
在直角中,,,
∴,,
∵,
∴,且,
∴是等边三角形,边长是,
∴,即图中阴影部分的面积是.
23.解:设的外接圆为,
当点在圆内,则,
当点在圆外,则,
∵,
∴点在圆上,
∴和有公共外接圆.
24.解:他们两个人的位置对球门的张角一样大.因为根据圆周角定义得.
25.证明:连接,
由圆周角定理得,,
∵,
∴,
∵,
∴,
∴是的切线;解:扇形的面积,
∵,,
∴,,
的面积,
的面积,
∴阴影部分的面积.
26.证明:连接.
∵是的切线,
∴,
∴,
即:.?
∵,
∴.
∴.
∵,
∴.
∴,
∴,即是等腰三角形.????????????????????
解:
成立.
连接.
∵是的切线,
∴,
∴,即:.??????????????
∵,
∴.
∵,
∴.
∵,
∴.
∴,
∴.
∴,即是等腰三角形.????????????????????
第三章 圆 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.一只蚂蚁以每分钟厘米的速度在地面上爬行,如果它在分钟内爬行了一周,那么它爬过的最大面积约是( )平方厘米.
A. B. C. D.
?2.已知在等腰三角形中,,底边,若以顶点为圆心,以为半径作,则与
A.相交 B.相切 C.相离 D.不能确定
?3.下列说法正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线只有一条
C.圆的切线垂直于圆的半径 D.每个三角形都有一个内切圆
?4.如图,已知是的直径,是弦,,过圆心作交弧于点,连接,则的度数为( )度.
A. B. C. D.
?5.已知是的内接三角形,为直径,,,平分角于,为的内心,则的长度为( )
A. B. C. D.
?6.如图,,是的切线,切点分别为,,点在上,且是优弧,则等于( )
A. B.
C. D.
?7.下列结论正确的是( )
A.垂直于弦的弦是直径 B.圆心角等于圆周角的倍
C.平分弦的直径垂直该弦 D.圆内接四边形的对角互补
?8.如图内接于,,是的两条切线,已知,,则的弧度数为( )
A. B. C. D.
?9.如图,一块含有角的直角三角板,在水平桌面上绕点接顺时针方向旋转到的位置.若,那么顶点从开始到结束所经过的路径长为( )
A. B. C. D.
?10.如图,点在的直径延长线上,与相切,切点为,点在上,连接、,已知.下列结论:
与相切;四边形是菱形;;.
其中,正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.若正六边形的边长为,则正六边形的半径为________;周长为________;边心距为________.
?12.如图,四边形是的内接四边形,是的延长线,若,则________.
?13.某校计划在校园内修建一座周长为的花坛,同学们设计出正三角形,正方形和圆三种图案,通过计算说明使花坛面积最大的图案是________(填图形).?
14.如图,中,,,.若以为圆心,为半径的弧交斜边与点,则弧的长为________.
?15.在中,,,,是中线,以为圆心,以长为半径画圆,则点与的位置关系是________.
?16.如图,,,是上三点,当平分时,能得出结论:________(任写一个).
?17.如图,四边形是矩形,的半径为,,,则图中阴影部分的面积约为________.(精确到)
18.如图,弦于,,,半径为,则长为________.
19.如图,在平面直角坐标系中,一条圆弧经过网格点、、,其中点坐标为,则该圆弧所在圆的圆心的坐标为________.
?20.一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是米,测得,垂足为,且米,则水平面宽________米.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.已知在四边形中,,能否画出一个圆,使它的四个顶点都在同一个圆上?
?
22.如图,是半径为的外一点,,是的切线,为切点,弦,连接,求阴影部分的面积.
?
23.已知:,在同侧,且.求证:和有公共外接圆.
?
24.足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲,乙两名运动员分别在,两处,他们争论不休,都说在自己所在的位置对球门的张角大,如果你是教练,请评一评他们两个人谁的位置对球门的张角大?为什么?
?
25.如图,点、、都在半径为的上,过点作交的延长线于点,连接,已知.
求证:是的切线;
求图中阴影部分的面积.
?
26.如图①已知是直径,是上一点(与、不重合),,垂足为,直线交于点,过点作的切线交直线于点,试证明:是等腰三角形;26.
对第题,当点在的延长线上时,其他条件不变;如图②,中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
答案
1.A
2.B
3.D
4.A
5.B
6.C
7.D
8.A
9.D
10.A
11.
12.
13.圆
14.
15.在上
16.
17.
18.
19.
20.
21.解:能画出一个圆,使它的四个顶点都在同一个圆上.
的外接圆为,假设点不在上(在外或内),如图,当点在外,交于,连接,
因为,而,所以,同样当点在内时也得到这与圆内接四边形的性质相矛盾,所以假设错误,所以点在上,即在四边形中,,能画出一个圆,使它的四个顶点都在同一个圆上.
22.解:连接,,
∵是圆的切线,
∴,
在直角中,,,
∴,,
∵,
∴,且,
∴是等边三角形,边长是,
∴,即图中阴影部分的面积是.
23.解:设的外接圆为,
当点在圆内,则,
当点在圆外,则,
∵,
∴点在圆上,
∴和有公共外接圆.
24.解:他们两个人的位置对球门的张角一样大.因为根据圆周角定义得.
25.证明:连接,
由圆周角定理得,,
∵,
∴,
∵,
∴,
∴是的切线;解:扇形的面积,
∵,,
∴,,
的面积,
的面积,
∴阴影部分的面积.
26.证明:连接.
∵是的切线,
∴,
∴,
即:.?
∵,
∴.
∴.
∵,
∴.
∴,
∴,即是等腰三角形.????????????????????
解:
成立.
连接.
∵是的切线,
∴,
∴,即:.??????????????
∵,
∴.
∵,
∴.
∵,
∴.
∴,
∴.
∴,即是等腰三角形.????????????????????
