5.2 统计的简单应用课时作业（2）

5.2统计的简单应用课时作业（2）
学校:___________姓名：___________班级：___________考号：___________
一、选择题
1．要反映武汉市某月每天的最低气温的变化趋势，宜采用（ ）
A． 条形统计图 B． 折线统计图 C． 扇形统计图 D． 频数分布统计图
2．在某公益活动中，小明对本班同学的捐款情况进行了统计，绘制成如下不完整的统计图．其中捐100元的人数占全班总人数的，则本次捐款的中位数是（ ）元.
A．10 B．20 C．50 D．100
3．用统计图来描述某班同学的身高情况，最合适的是（ ）
A． 频数分布直方图 B． 条形统计图 C． 扇形统计图 D． 折线统计图
4．为了解我市居民在春节期间的消费所占家庭收入的比例情况，某调查机构抽查了我市2000户家庭的消费情况进行统计，则下列说法不正确的是（ ）
A． 最好不选择折线统计图和条形统计图
B． 2000户家庭的消费情况是总体
C． 本次调查的样本容量是2000
D． 本次调查是抽样调查
5．(龙岩中考改编)下列统计图能够显示数据变化趋势的是( )
A．条形图 B．扇形图 C．折线图 D．以上都正确
6．数学老师对黄华的8次单元考试成绩进行统计分析，要判断黄华的数学成绩是否稳定，老师需要知道黄华这8次数学成绩的（ ）
A．平均数 B．中位数 C．众数 D．方差
二、填空题
7．期末考试后，小红将本班50名学生的数学成绩进行分类统计，得到如图的扇形统计图，则优生人数为　 　．
8．用___________统计图，反映某学生从6岁到12岁每年一次检查的视力情况.
用___________统计图，反映某班40名同学穿鞋的码数.
用___________统计图，反映某市五个区的战地面积与全市总面积的对比情况.
9．某学校七(3)班40位同学都订阅了杂志，10%的同学订阅《科学画报》，40%的同学订阅《作文通讯》，30%的同学订阅《英语画刊》，20%的同学订阅其他杂志．能表示上述数据的统计图是_________统计图．
10．下列几项调查中，比较适合普查的项有 .
（1）调查1000台同批次电视机的平均寿命；
（2）审查书稿有哪些科学性错误；
（3）环保部门对新安江苯酚泄漏污染情况的调查；
（4）学校在给学生做校服前对尺寸大小的调查.
11．甲、乙、丙三台机床生产直径为60mm的螺丝，为了检验产品质量，从三台机床生产的螺丝中各抽取了20个测量其直径，进行数据处理后，发现三组数据的平均数都是60mm，它们的方差依次为，，，根据以上提供的信息，你认为生产螺丝的质量最好的是_____________机床.
三、解答题
12．QQ运动记录的小莉爸爸2017年2月份7天步行的步数（单位：万步）如下表：
日期
2月6日
2月7日
2月8日
2月9日
2月10日
2月11日
2月12日
步数
2.1
1.7
1.8
1.9
2.0
1.8
2.0
（1）制作适当的统计图表示小莉爸爸这7天步行的步数的变化趋势；
（2）求小莉爸爸这7天中每天步行的平均步数；
（3）估计小莉爸爸2月份步行的总步数．
13．据统计两省人口总数基本相同，2001年A省的城镇在校中学生人数为156万，农村在校中学生人数为72万；B省的城镇在校中学生人数为84万，农村在校中学生人数为103万李军同学根据数据画出下面两个复合条形统计图．

图______ 更好反映两省在校中学生总数；
图______ 更好地比较省城镇和农村在校中学生人数；
说说两种图的特点．
14．甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相同．比赛结束后，发现参赛学生成绩分别为7分、8分、9分、10分（满分为10分）．
依据统计数据绘制了如下尚不完整的统计图表．
（1）在图1中，“7分”所在扇形的圆心角等于 度；将图2的统计图补充完整；
（2）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数，并从平均分和中位数的角度分析哪所学校的成绩较好；
（3）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校合适？
15．原创大型文化情感类节目《朗读者》在中央电视台综合频道、综艺频道播出后引起社会各界强烈反响，小明想了解本小区居民对《朗读者》的看法，进行了一次抽样调查，把居民对《朗读者》的看法分为四个层次：A．非常喜欢；B．较喜欢；C．一般；D．不喜欢；并将调查结果绘制了图1和图2两幅不完整的统计图．
请你根据图中提供的信息解答下列问题：
（1）本次调查的居民总人数为=_____人；
（2）将图1和图2补充完整；
（3）图2中“C”层次所在扇形的圆心角的度数为_____；
（4）估计该小区4000名居民中对《朗读者》的看法表示喜欢（包括A层次和B层次）的大约有_____人．
16．为了方便居民低碳出行，2016年10月1日起，聊城市公共自行车租赁系统（一期）试运行，越来越多的居民选择公共自行车作为出行的交通工具，市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况，随机抽取了该小区部分居民进行调查，并绘制了如图的条形统计图和扇形统计图（部分信息未给出）
请根据上面的统计图，解答下列问题：
（1）被调查的总人数是 ______ 人；
（2）公共自行车租赁系统运行后，被调查居民选择自行车作为出行方式的百分比提高了多少？
（3）如果该小区共有居民2000人，公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人？
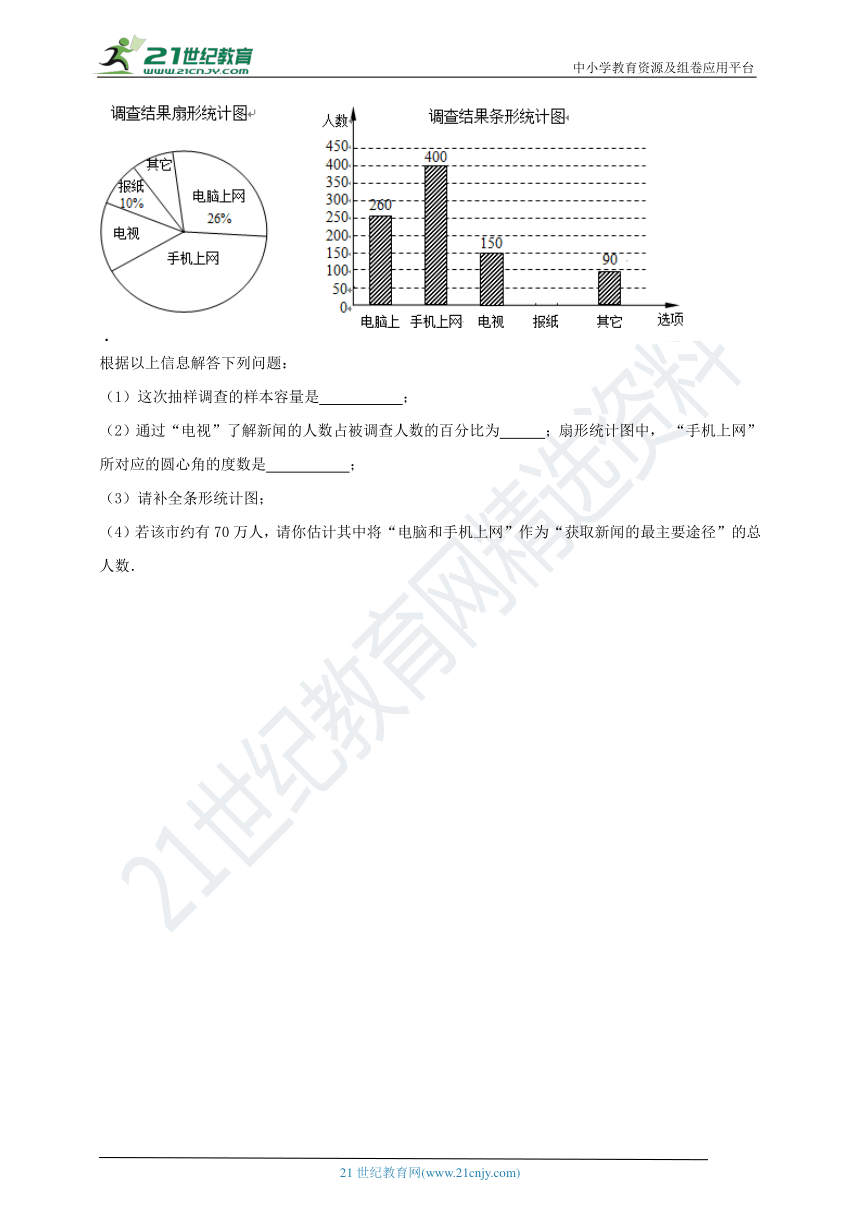
17．为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图．
根据以上信息解答下列问题：
（1）这次抽样调查的样本容量是 ；
（2）通过“电视”了解新闻的人数占被调查人数的百分比为 ；扇形统计图中， “手机上网”所对应的圆心角的度数是 ；
（3）请补全条形统计图；
（4）若该市约有70万人，请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数．
参考答案
1．B
【解析】
【分析】
扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目，根据统计图的特点进行分析即可得出答案.
【详解】
要反映武汉市某月每天的最低气温的变化趋势，宜采用折线统计图，
故选B．
【点睛】
本题主要考查统计图的选择.根据扇形统计图、折线统计图、条形统计图各自的特点来判断是解题的关键．
2．B
【解析】捐100元的人数占全班总人数的，则捐款的总人数为15÷=60人，则由图可知，捐20元的为60-20-10-15=15人，将捐款人按捐款数从少到多排列，则中位数为20元.
3．A
【解析】
分析：根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．
详解：用统计图来描述某班同学的身高情况，最合适的是频数分布直方图．
故选：A．
点睛：此题主要考查了统计图的选择，根据扇形统计图、折线统计图、条形统计图各自的特点来判断是解题关键．
4．B
【解析】试题分析：A、调查春节期间的消费占家庭收入的比例情况宜采用直方图进行统计，最好不选择折线统计图和条形统计图，故此选项正确；
B、2000户家庭的消费情况是样本，故此选项错误；
C、查了我市2000户家庭的消费情况进行统计，本次调查的样本容量是2000，故此选项正确；
D、本次调查是抽样调查，故此选项正确．
故选B．
5．C
【解析】易于显示数据的变化趋势和变化规律的统计图是折线统计图,故选C.
6．D
【解析】
试题分析：方差是反映一组数据的波动情况．
考点：方差的左右．
7．10
【解析】先求出不及格人数所占的百分比，然后乘以总人数即可
8．折线条形扇形
【解析】
【分析】
根据各种统计图的特征解答即可.
【详解】
折线统计图能清楚地反映事物的变化情况，条形统计图能清楚地表示出每个项目的具体数目，扇形统计图能清楚地表示出各部分在总体中所占的百分比，由此可得：①用折线统计图，反映某学生从6岁到12岁每年一次检查的视力情况；②用条形统计图，反映某班40名同学穿鞋的码数；③用扇形统计图，反映某市五个区的战地面积与全市总面积的对比情况.
故答案为：折线；条形；扇形.
【点睛】
本题考查了统计图的选择，在选择统计图时，要根据题目中的数据特点及题目要求进行合理选择．
9．扇形
【解析】解析：扇形统计图能够直观地反映各部分占全体的比例，故上述数据适合用扇形统计图表示.
10．（2）（4）
【解析】本题考查的是普查与抽样调查
一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
（1）调查具有破坏性，必须使用抽样调查；
（2）因为调查的对象比较重要，故应采用普查的方式；
（3）范围比较大，普查很困难，应选择抽样调查；
（4）学生人数不多，适合普查；
故比较适合普查的项有（2）（4）．
11．乙
【解析】由于在这三台机床中，乙的方差最小，所以乙机床生产的螺丝质量最好．故答案为乙．
12．（1）见解析；（2）1.9万步；（3）53.2万步.
【解析】分析：（1）直接利用折线统计图画出符合题意的答案；
（2）直接利用平均数求法得出答案；
（3）利用样本平均数估计总体平均数即可．
详解：（1）用折线统计图表示小莉爸爸这7天内步行的步数如下：
；
（2）小莉爸爸这7天内每天步行的平均步数为：
×（2.1+1.7+1.8+1.9+2.0+1.8+2.0）=1.9（万步）．
（3）小莉爸爸2月份步行的步数约为：1.9×28=53.2（万步）．
点睛：此题主要考查了统计图的选择以及利用样本估计总体，正确理解样本估计总的意义是解题关键．
13．（1） （2） (3)答案详见解析.
【解析】试题分析：（1）（2）根据两个图直接可以写出答案；
（3）根据（1）、（2）比较的结果写出即可．
试题解析：
解：（1）图（2）更好反映两省在校中学生总数；
故答案为：（2）；
（2）图（1）更好地比较A（B）省城镇和农村在校中学生人数；
故答案为：（1）；
（3）图（1）更直观地反映本省城镇与农村在校中学生人数的差别；
图（2）更好反映两省在校中学生总数的差别．
点睛：本题考查读复合型条形图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
14．（1）144（2）乙校的成绩较好（3）甲校
【解析】试题分析：（1）根据扇形统计图中所标的圆心角的度数进行计算；根据10分所占的百分比是90°÷360°=25%计算总人数，再进一步求得8分的人数，即可补全条形统计图；
（2）根据乙校人数得到甲校人数，再进一步求得其9分的人数，从而求得平均数和中位数，并进行综合分析；
（3）观察两校的高分人数进行分析．
试题解析：（1）利用扇形图可以得出：
“7分”所在扇形的圆心角=360°-90°-72°-54°=144°；
利用扇形图：10分所占的百分比是90°÷360°=25%，
则总人数为：5÷25%=20（人），
得8分的人数为：20×=3（人）．
如图；
（2）根据乙校的总人数，知甲校得9分的人数是20-8-11=1（人）．
甲校的平均分：（7×11+9+80）÷20=8.3分；
中位数为7分．
由于两校平均分相等，乙校成绩的中位数大于甲校的中位数，所以从平均分和中位数角度上判断，乙校的成绩较好．
（3）因为选8名学生参加市级口语团体赛，甲校得（10分）的有8人，而乙校得（10分）的只有5人，所以应选甲校．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
理解中位数和众数的概念．
15． 300； 见解析 72°；
【解析】（1）根据A层次的有90人，所占的百分比是30%，据此即可求得调查的总人数；
（2）利用总人数乘以对应的百分比求得C层次的人数，然后用总人数减去其它层次的人数求得B层次的人数，从而补全直方图；
（3）利用360°乘以对应的百分比求得所在扇形的圆心角的度数；
（4）利用总人数乘以对应的比例即可求解．
解：（1）抽查的总人数是90÷30%=300（人）；
故答案为：300；
（2）C层次的人数是300×20%=60（人），
则B层次的人数是300﹣90﹣60﹣30=120（人），所占的百分比是=40%，
D层次所占的百分比是=10%．
；
（3）“C”层次所在扇形的圆心角的度数是360°×=72°；
故答案为：72°；
（4）对“广场舞”的看法表示赞同（包括A层次和B层次）的大约4000×=2800（人）．
答：估计对“广场舞”的看法表示赞同的大约有2800人．
故答案为：2800．
16．（1）50；（2）20%；（3）1000人
【解析】试题分析：（1）根据条形图的数据计算即可；
（2）计算出共自行车租公赁系统运行前、后的百分比，计算即可；
（3）用样本估计总体即可．
试题解析：（1）由条形图可知，被调查的总人数是10+15+25=50人，
（2）共自行车租公赁系统运行前，居民选择自行车作为出行方式的百分比为：15÷50=30%，
公共自行车租赁系统运行后，居民选择自行车作为出行方式的百分比为：100%-36%-14%=50%，
50%-30%=20%，
答：公共自行车租赁系统运行后，被调查居民选择自行车作为出行方式的百分比提高了20%；
（3）公共自行车租赁系统运行后估计选择自行车作为出行方式的有：2000×50%=1000人．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
17．（1）1000；
（2）15％ 144°；
（3）补全条形统计图见解析；
（4）将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数462000人.
【解析】试题分析: （1）根据“电脑上网”的人数和所占的百分比求出总人数；
（2）用“电视”的数量除以总数求出所占的百分比,用“手机上网”所占的百分比乘以360°，即可得出答案；
（3）用总人数乘以“报纸”所占百分比，求出“报纸”的人数，从而补全统计图；
（4）用全市的总人数乘以“电脑和手机上网”所占的百分比，即可得出答案．
试题解析：（1）这次接受调查的市民总人数是：260÷26％=1000
（2）扇形统计图中，通过“电视”了解新闻的人数占被调查人数的百分比为： =15％, =144°；
（3）“报纸”的人数为：1000×10%=100.
补全图形如图所示：
（4）估计将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数为：
70×(26%+40%)=70×66%=46.2(万人).
∴将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数为462000人.