关于球的内切和外接专题讲座
图片预览



文档简介
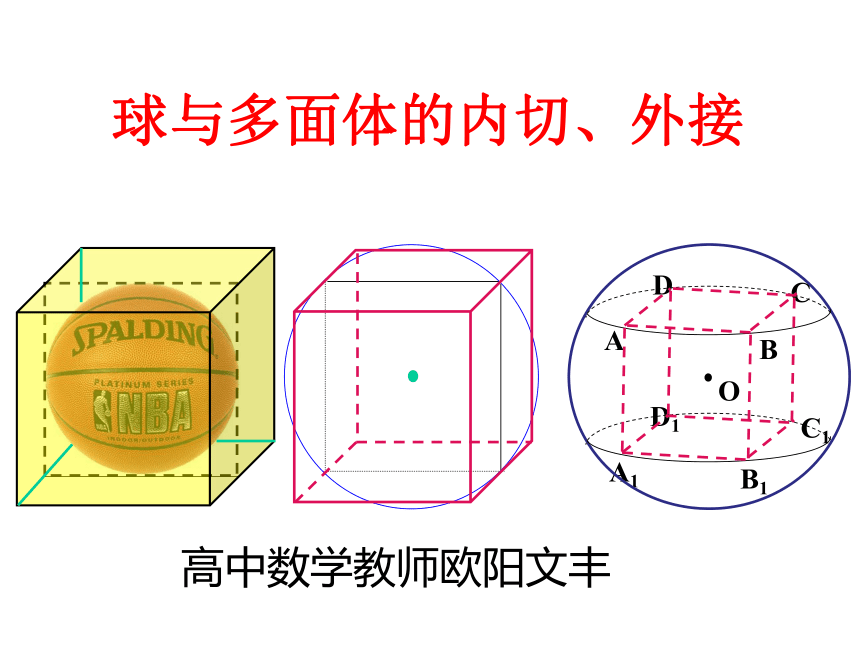
球与多面体的内切、外接
高中数学教师欧阳文丰
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个多面体的内切球。
一、复习
球体的体积与表面积
解决“接切”问题的关键是画出正确的截面,把空间“接切”转化为平面“接切”问题
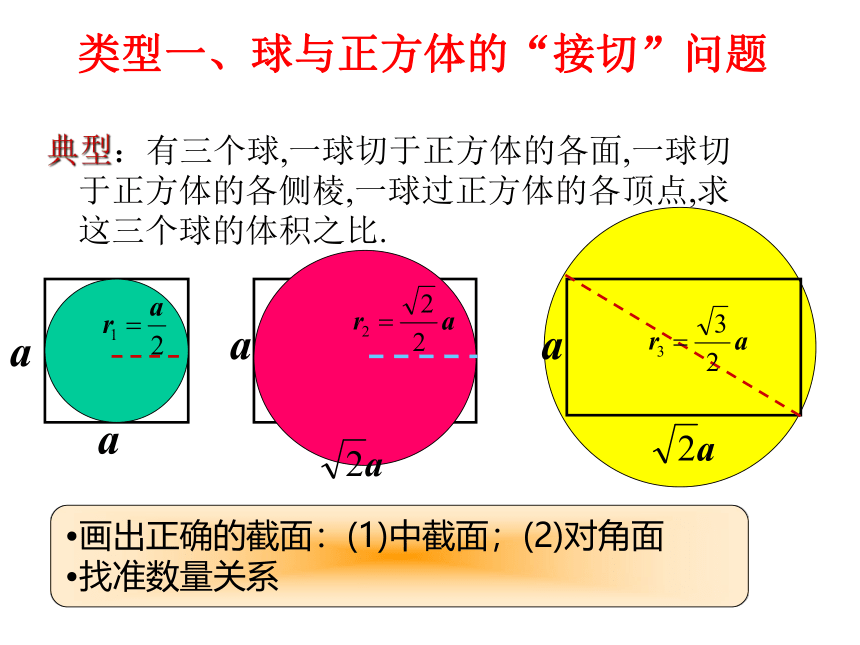
类型一、球与正方体的“接切”问题
典型:有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.
画出正确的截面:(1)中截面;(2)对角面
找准数量关系
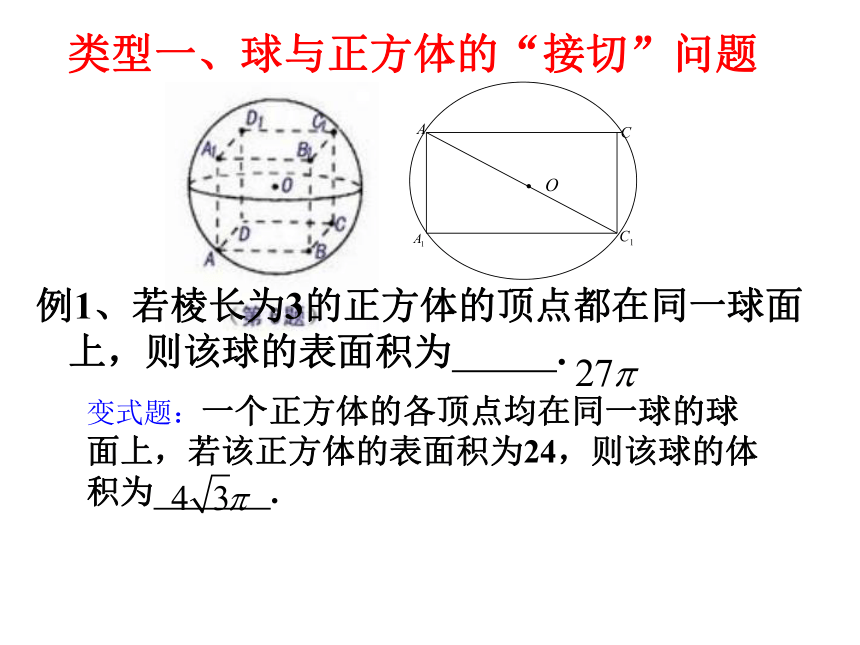
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
类型一、球与正方体的“接切”问题
类型二、求长方体外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
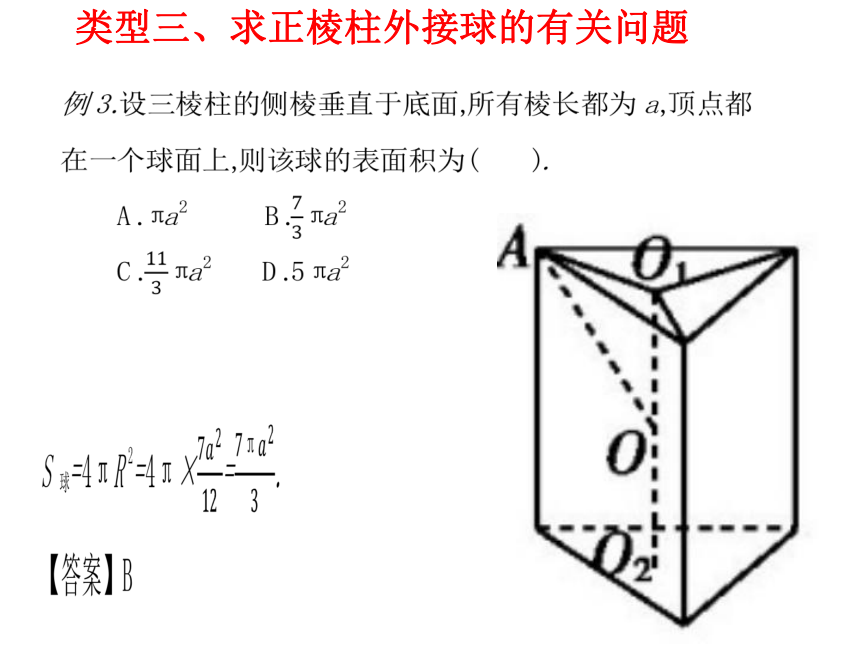
类型三、求正棱柱外接球的有关问题
类型三、求正棱柱外接球的有关问题
类型三、求正棱柱外接球的有关问题
1、三棱柱
各顶点都在一个球面上,侧棱与底面垂直,
,
,则这个球的表面积为
. 64
2、在三棱锥
中,
,
,则三棱锥
外接球的表面积 .
类型三、求正棱柱外接球的有关问题
变式练习
正棱锥、四面体与球的“接切”问题
典型:正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等
2、正多面体的内切球和外接球的球心重合
3、正棱锥的内切球和外接球球心都在高线上,但不重合
4、基本方法:构造三角形利用相似比和勾股定理
5、体积分割是求内切球半径的通用做法
1
过侧棱AB与球心O作截面( 如图 )
在正三棱锥中,BE 是正△BCD的高,
O1 是正△BCD的中心,且AE 为斜高
解法1:
作 OF ⊥ AE 于 F
设内切球半径为 r,则 OA = 1 -r
∵ Rt △ AFO ∽ Rt △ AO1E
类型四、求正棱锥的外接球和内切球有关问题
设球的半径为 r,则 VA- BCD =
VO-ABC + VO- ABD + VO-ACD + VO-BCD
解法2:
类型四、求正棱锥的外接球和内切球有关问题
例6、求棱长为1的正四面体外接球的体积.
类型四、求正棱锥的外接球和内切球有关问题
例7、正四棱锥S-ABCD的底面边长和各侧棱长都为 ,点S,A,B,C,D都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为 ,外接球的球心为O,如图3所示.∴由球的截面的性质,
可得
又 ,∴球心O必在 所在的直线上.
∴ 的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.
在 中,由
是外接圆的半径,也是外接球的半径.故
类型四、求正棱锥的外接球和内切球有关问题
球的内切、外接问题
5、体积分割是求内切球半径的通用做法。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不 重合。
4、基本方法:构造三角形利用相似比和勾股定理。
6、正四面体的棱长为a,则正四面体的高为 ,其外
接球的半径为 ,内切球的半径为 。
高中数学教师欧阳文丰
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个多面体的内切球。
一、复习
球体的体积与表面积
解决“接切”问题的关键是画出正确的截面,把空间“接切”转化为平面“接切”问题
类型一、球与正方体的“接切”问题
典型:有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.
画出正确的截面:(1)中截面;(2)对角面
找准数量关系
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
类型一、球与正方体的“接切”问题
类型二、求长方体外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
类型三、求正棱柱外接球的有关问题
类型三、求正棱柱外接球的有关问题
类型三、求正棱柱外接球的有关问题
1、三棱柱
各顶点都在一个球面上,侧棱与底面垂直,
,
,则这个球的表面积为
. 64
2、在三棱锥
中,
,
,则三棱锥
外接球的表面积 .
类型三、求正棱柱外接球的有关问题
变式练习
正棱锥、四面体与球的“接切”问题
典型:正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等
2、正多面体的内切球和外接球的球心重合
3、正棱锥的内切球和外接球球心都在高线上,但不重合
4、基本方法:构造三角形利用相似比和勾股定理
5、体积分割是求内切球半径的通用做法
1
过侧棱AB与球心O作截面( 如图 )
在正三棱锥中,BE 是正△BCD的高,
O1 是正△BCD的中心,且AE 为斜高
解法1:
作 OF ⊥ AE 于 F
设内切球半径为 r,则 OA = 1 -r
∵ Rt △ AFO ∽ Rt △ AO1E
类型四、求正棱锥的外接球和内切球有关问题
设球的半径为 r,则 VA- BCD =
VO-ABC + VO- ABD + VO-ACD + VO-BCD
解法2:
类型四、求正棱锥的外接球和内切球有关问题
例6、求棱长为1的正四面体外接球的体积.
类型四、求正棱锥的外接球和内切球有关问题
例7、正四棱锥S-ABCD的底面边长和各侧棱长都为 ,点S,A,B,C,D都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为 ,外接球的球心为O,如图3所示.∴由球的截面的性质,
可得
又 ,∴球心O必在 所在的直线上.
∴ 的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.
在 中,由
是外接圆的半径,也是外接球的半径.故
类型四、求正棱锥的外接球和内切球有关问题
球的内切、外接问题
5、体积分割是求内切球半径的通用做法。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不 重合。
4、基本方法:构造三角形利用相似比和勾股定理。
6、正四面体的棱长为a,则正四面体的高为 ,其外
接球的半径为 ,内切球的半径为 。
