2018-2019学年人教版九年级上《24.1.4圆周角》同步练习含答案
文档属性
| 名称 | 2018-2019学年人教版九年级上《24.1.4圆周角》同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-03 00:00:00 | ||
图片预览




文档简介
2018-2019学年度人教版数学九年级上册同步练习
24.1.4 圆周角
一.选择题(共12小题)
1.如图,A,B,C是⊙O上的三点,∠ABO=25°,∠ACO=30°,则∠BOC的度数为( )
A.100° B.110° C.125° D.130°
2.如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,则∠ACD的度数为( )
A.46° B.23° C.44° D.67°
3.如图,AB是圆O的弦,AB=20,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN的最大值是( )
A.10 B.5 C.10 D.20
4.如图,在⊙O中,弧AB=弧AC,∠A=36°,则∠C的度数为( )
A.44° B.54° C.62° D.72°
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,∠BAC=30°,弧BC等于弧CD,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
6.如图,⊙O中,若∠BOD=140°,∠CDA=30°,则∠AEC的度数是( )
A.80° B.100° C.110° D.125°
7.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A. B. C. D.
8.如图,AB是⊙O直径,若∠AOC=130°,则∠D的度数是( )
A.20° B.25° C.40° D.50°
9.如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F,连接BF,CF,若∠EDC=135°,CF=2,则AE2+BE2的值为( )
A.8 B.12 C.16 D.20
10.如图,AB是⊙O的直径,C是⊙O上一点(A、B除外),∠AOD=130°,则∠C的度数是( )
A.50° B.60° C.25° D.30°
11.如图,AB经过圆心O,四边形ABCD内接于⊙O,∠B=3∠BAC,则∠ADC的度数为( )
A.100° B.112.5° C.120° D.135°
12.如图,四边形ABCD内接于⊙O,∠DAB=140°,连接OC,点P是半径OC上一点,则∠BPD不可能为( )
A.40° B.60° C.80° D.90°
二.填空题(共6小题)
13.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为 .
14.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 .
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,(1)若CD=16,BE=4,则⊙O的半径为 ;(2)点M在⊙O上,MD恰好经过圆心O,连接MB,若∠M=∠D,则∠D的度数为 .
16.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE= .
17.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,∠ABC=40°,则∠BCD的度数为
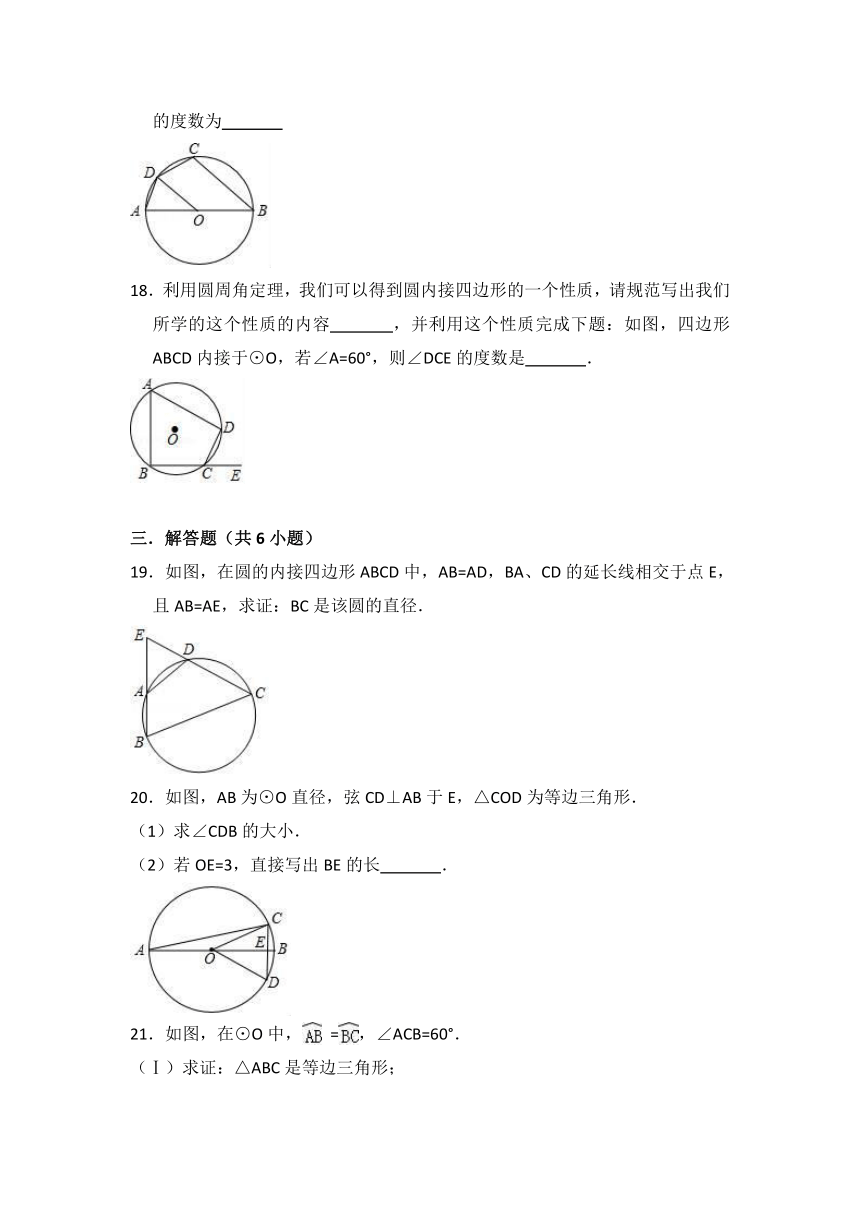
18.利用圆周角定理,我们可以得到圆内接四边形的一个性质,请规范写出我们所学的这个性质的内容 ,并利用这个性质完成下题:如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE的度数是 .
三.解答题(共6小题)
19.如图,在圆的内接四边形ABCD中,AB=AD,BA、CD的延长线相交于点E,且AB=AE,求证:BC是该圆的直径.
20.如图,AB为⊙O直径,弦CD⊥AB于E,△COD为等边三角形.
(1)求∠CDB的大小.
(2)若OE=3,直接写出BE的长 .
21.如图,在⊙O中, =,∠ACB=60°.
(Ⅰ)求证:△ABC是等边三角形;
(Ⅱ)求∠AOC的大小.
22.已知四边形ABCD是圆内接四边形,∠1=112°,求∠CDE.
23.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
24.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
参考答案与试题解析
一.选择题(共12小题)
1.【解答】解:过A作⊙O的直径,交⊙O于D.
在△OAB中,OA=OB,
则∠BOD=∠ABO+∠OAB=2×25°=50°,
同理可得:∠COD=∠ACO+∠OAC=2×30°=60°,
故∠BOC=∠BOD+∠COD=110°.
故选:B.
2.【解答】解:连接OD,
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,
∴点A,B,C,D共圆,
∵点D对应的刻度是46°,
∴∠BOD=46°,
∴∠BCD=∠BOD=23°,
∴∠ACD=90°﹣∠BCD=67°.
故选:D.
3.【解答】解:连接OA、OB,如图,
∴∠AOB=2∠ACB=2×45°=90°,
∴△OAB为等腰直角三角形,
∴OA=AB=×20=20,
∵点M、N分别是AB、BC的中点,
∴MN=AC,
当AC为直径时,AC的值最大,
∴MN的最大值为20.
故选:D.
4.【解答】解:∵⊙O中,,∠A=36°,
∴∠B=∠C=72°,
故选:D.
5.【解答】解:∵∠BAC=30°
∴弧BC的度数是30°,
∵弧BC等于弧CD
∴∠DAC=30°.
故选:A.
6.【解答】解:由圆周角定理得,∠C=∠BOD=70°,
∴∠AEC=∠C+∠CDA=100°,
故选:B.
7.【解答】解:连接OC、OA、BD,作OH⊥AC于H.
∵∠AOC=2∠ABC=120°,
∵OA=OC,OH⊥AC,
∴∠COH=∠AOH=60°,CH=AH,
∴CH=AH=OC?sin60°=,
∴AC=2,
∵CN=DN,DM=AM,
∴MN=AC=,
∵CP=PB,AN=DN,
∴PN=BD,
当BD是直径时,PN的值最大,最大值为2,
∴PM+MN的最大值为2+.
故选:D.
8.【解答】解:连接AD,
∵AB是⊙O直径,∠AOC=130°,
∴∠BDA=90°,∠CDA=65°,
∴∠BDC=25°,
故选:B.
9.【解答】解:∵四边形BCDE内接于⊙O,且∠EDC=135°,
∴∠EFC=∠ABC=180°﹣∠EDC=45°,
∵∠ACB=90°,
∴△ABC是等腰三角形,
∴AC=BC,
又∵EF是⊙O的直径,
∴∠EBF=∠ECF=∠ACB=90°,
∴∠BCF=∠ACE,
∵四边形BECF是⊙O的内接四边形,
∴∠AEC=∠BFC,
∴△ACE≌△BFC(ASA),
∴AE=BF,
∵Rt△ECF中,CF=2、∠EFC=45°,
∴EF2=16,
则AE2+BE2=BF2+BE2=EF2=16,
故选:C.
10.【解答】解:∵∠AOD=130°,
∴∠C=90°﹣,
故选:C.
11.【解答】解:∵AB经过圆心O,
∴∠ACB=90°,
∵∠B=3∠BAC,
∴∠B=67.5°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°﹣∠B=112.5°,
故选:B.
12.【解答】解:连接OD、OB,
∵四边形ABCD内接于⊙O,
∴∠DCB=180°﹣∠DAB=40°,
由圆周角定理得,∠BOD=2∠DCB=80°,
∴40°≤∠BPD≤80°,
∴∠BPD不可能为90°,
故选:D.
二.填空题(共6小题)
13.【解答】解:由圆周角定理得,∠AOD=2∠ACD=50°,
∴∠BOD=180°﹣50°=130°,
故答案为:130°.
14.【解答】解:在优弧BD上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故答案为100°.
15.【解答】解:(1)设⊙O的半径为r,则OE=r﹣4,
∵AB是⊙O的直径,弦CD⊥AB,
∴DE=EC=CD=8,
在Rt△OED中,OD2=OE2+DE2,即r2=(r﹣4)2+82,
解得,r=10,
故答案为:10;
(2)由圆周角定理得,∠DOE=2∠M,
∵∠M=∠D,
∴∠DOE=2∠D,
∴∠D=30°,
故答案为:30°.
16.【解答】解:连接OB,OD,
∵∠DOB与∠A都对,∠DOB(大于平角的角)与∠BCD都对,
∴∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,
∵∠DOB+∠DOB(大于平角的角)=360°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A=102°,
故答案为:102°
17.【解答】解:∵OD∥BC,
∴∠AOD=∠ABC=40°,
∵OA=OD,
∴∠OAD=∠ODA=70°,
∵四边形ABCD内接于⊙O,
∴∠BCD=180°﹣∠OAD=110°,
故答案为:110°.
18.【解答】解:∵圆内接四边形的对角互补,
∴∠A+∠BCD=180°,
∵∠A=60°,
∴∠BCD=120°,
∴∠DCE=180°﹣∠BCD=60°,
故答案为;圆内接四边形的对角互补,60°.
三.解答题(共6小题)
19.【解答】解:连接BD.
∵AE=AD=AB,
∴∠E=∠ADE,∠ADB=∠ABD,
∵∠E+∠EDB+∠ABD=180°,
∴2∠EDA+2∠ADB=180°,
∴∠EDA+∠ADB=90°,
∴∠BDC=∠EDB=90°,
∴BC是该圆的直径.
20.【解答】解:(1)∵△OCD是等边三角形
∴OC=OD=CD,∠OCD=∠ODC=∠COD=60°
∵OB⊥CD
∴∠COB=30°
∵∠COB=2∠CDB
∴∠CDB=15°
(2)∵sin∠OCD==
∴
∴OC=2
∴BE=OB﹣BE=2﹣3
故答案为2﹣3.
21.【解答】(Ⅰ)证明:∵=,
∴AB=BC,又∠ACB=60°,
∴△ABC是等边三角形;
(Ⅱ)∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°.
22.【解答】解:由圆周角定理得,∠A=∠1=56°,
∵四边形ABCD是圆内接四边形,
∴∠CDE=∠A=56°.
23.【解答】解:(1)∵∠BCD=120°,CA平分∠BCD,
∴∠ACD=∠ACB=60°,
由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,
∴△ABD是等边三角形;
(2)连接OB、OD,作OH⊥BD于H,
则DH=BD=,
∠BOD=2∠BAD=120°,
∴∠DOH=60°,
在Rt△ODH中,OD==,
∴⊙O的半径为.
24.【解答】解:(1)证明:∵∠ABC=90°,点M是AC的中点,
∴AM=CM=BM.
∴∠A=∠ABM.
∵四边形DEBA为⊙O的内接四边形,
∴∠ADE+∠ABM=180°,
又∵∠ADE+∠MDE=180°,
∴∠ABM=∠MDE
∴∠A=∠ABM=∠MDE.
(2)解:由(1)知∠A=∠ABM=∠MDE,
∴DE∥AB
∴△MDE∽△MAB
∴=
∵AD=2DM,∴AM=3DM
∴=
∴DE=2.
(3)证明:由(1)知∠A=∠ABM=∠MDE,
∵∠A=60°,∴∠A=∠ABM=∠MDE=60°
∴∠AMB=60°
又∵OA=OD=OE=OB
∴△AOD、△OBE都是等边三角形
∴∠ADO=∠AMB=∠OEB=60°,
∴OD∥BM,AM∥OE
∴四边形ODME是平行四边形,
又∵OD=OE
∴四边形ODME是菱形
24.1.4 圆周角
一.选择题(共12小题)
1.如图,A,B,C是⊙O上的三点,∠ABO=25°,∠ACO=30°,则∠BOC的度数为( )
A.100° B.110° C.125° D.130°
2.如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,则∠ACD的度数为( )
A.46° B.23° C.44° D.67°
3.如图,AB是圆O的弦,AB=20,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN的最大值是( )
A.10 B.5 C.10 D.20
4.如图,在⊙O中,弧AB=弧AC,∠A=36°,则∠C的度数为( )
A.44° B.54° C.62° D.72°
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,∠BAC=30°,弧BC等于弧CD,则∠DAC的度数是( )
A.30° B.35° C.45° D.70°
6.如图,⊙O中,若∠BOD=140°,∠CDA=30°,则∠AEC的度数是( )
A.80° B.100° C.110° D.125°
7.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A. B. C. D.
8.如图,AB是⊙O直径,若∠AOC=130°,则∠D的度数是( )
A.20° B.25° C.40° D.50°
9.如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F,连接BF,CF,若∠EDC=135°,CF=2,则AE2+BE2的值为( )
A.8 B.12 C.16 D.20
10.如图,AB是⊙O的直径,C是⊙O上一点(A、B除外),∠AOD=130°,则∠C的度数是( )
A.50° B.60° C.25° D.30°
11.如图,AB经过圆心O,四边形ABCD内接于⊙O,∠B=3∠BAC,则∠ADC的度数为( )
A.100° B.112.5° C.120° D.135°
12.如图,四边形ABCD内接于⊙O,∠DAB=140°,连接OC,点P是半径OC上一点,则∠BPD不可能为( )
A.40° B.60° C.80° D.90°
二.填空题(共6小题)
13.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为 .
14.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 .
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,(1)若CD=16,BE=4,则⊙O的半径为 ;(2)点M在⊙O上,MD恰好经过圆心O,连接MB,若∠M=∠D,则∠D的度数为 .
16.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE= .
17.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,∠ABC=40°,则∠BCD的度数为
18.利用圆周角定理,我们可以得到圆内接四边形的一个性质,请规范写出我们所学的这个性质的内容 ,并利用这个性质完成下题:如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE的度数是 .
三.解答题(共6小题)
19.如图,在圆的内接四边形ABCD中,AB=AD,BA、CD的延长线相交于点E,且AB=AE,求证:BC是该圆的直径.
20.如图,AB为⊙O直径,弦CD⊥AB于E,△COD为等边三角形.
(1)求∠CDB的大小.
(2)若OE=3,直接写出BE的长 .
21.如图,在⊙O中, =,∠ACB=60°.
(Ⅰ)求证:△ABC是等边三角形;
(Ⅱ)求∠AOC的大小.
22.已知四边形ABCD是圆内接四边形,∠1=112°,求∠CDE.
23.如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
24.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
参考答案与试题解析
一.选择题(共12小题)
1.【解答】解:过A作⊙O的直径,交⊙O于D.
在△OAB中,OA=OB,
则∠BOD=∠ABO+∠OAB=2×25°=50°,
同理可得:∠COD=∠ACO+∠OAC=2×30°=60°,
故∠BOC=∠BOD+∠COD=110°.
故选:B.
2.【解答】解:连接OD,
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,
∴点A,B,C,D共圆,
∵点D对应的刻度是46°,
∴∠BOD=46°,
∴∠BCD=∠BOD=23°,
∴∠ACD=90°﹣∠BCD=67°.
故选:D.
3.【解答】解:连接OA、OB,如图,
∴∠AOB=2∠ACB=2×45°=90°,
∴△OAB为等腰直角三角形,
∴OA=AB=×20=20,
∵点M、N分别是AB、BC的中点,
∴MN=AC,
当AC为直径时,AC的值最大,
∴MN的最大值为20.
故选:D.
4.【解答】解:∵⊙O中,,∠A=36°,
∴∠B=∠C=72°,
故选:D.
5.【解答】解:∵∠BAC=30°
∴弧BC的度数是30°,
∵弧BC等于弧CD
∴∠DAC=30°.
故选:A.
6.【解答】解:由圆周角定理得,∠C=∠BOD=70°,
∴∠AEC=∠C+∠CDA=100°,
故选:B.
7.【解答】解:连接OC、OA、BD,作OH⊥AC于H.
∵∠AOC=2∠ABC=120°,
∵OA=OC,OH⊥AC,
∴∠COH=∠AOH=60°,CH=AH,
∴CH=AH=OC?sin60°=,
∴AC=2,
∵CN=DN,DM=AM,
∴MN=AC=,
∵CP=PB,AN=DN,
∴PN=BD,
当BD是直径时,PN的值最大,最大值为2,
∴PM+MN的最大值为2+.
故选:D.
8.【解答】解:连接AD,
∵AB是⊙O直径,∠AOC=130°,
∴∠BDA=90°,∠CDA=65°,
∴∠BDC=25°,
故选:B.
9.【解答】解:∵四边形BCDE内接于⊙O,且∠EDC=135°,
∴∠EFC=∠ABC=180°﹣∠EDC=45°,
∵∠ACB=90°,
∴△ABC是等腰三角形,
∴AC=BC,
又∵EF是⊙O的直径,
∴∠EBF=∠ECF=∠ACB=90°,
∴∠BCF=∠ACE,
∵四边形BECF是⊙O的内接四边形,
∴∠AEC=∠BFC,
∴△ACE≌△BFC(ASA),
∴AE=BF,
∵Rt△ECF中,CF=2、∠EFC=45°,
∴EF2=16,
则AE2+BE2=BF2+BE2=EF2=16,
故选:C.
10.【解答】解:∵∠AOD=130°,
∴∠C=90°﹣,
故选:C.
11.【解答】解:∵AB经过圆心O,
∴∠ACB=90°,
∵∠B=3∠BAC,
∴∠B=67.5°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°﹣∠B=112.5°,
故选:B.
12.【解答】解:连接OD、OB,
∵四边形ABCD内接于⊙O,
∴∠DCB=180°﹣∠DAB=40°,
由圆周角定理得,∠BOD=2∠DCB=80°,
∴40°≤∠BPD≤80°,
∴∠BPD不可能为90°,
故选:D.
二.填空题(共6小题)
13.【解答】解:由圆周角定理得,∠AOD=2∠ACD=50°,
∴∠BOD=180°﹣50°=130°,
故答案为:130°.
14.【解答】解:在优弧BD上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故答案为100°.
15.【解答】解:(1)设⊙O的半径为r,则OE=r﹣4,
∵AB是⊙O的直径,弦CD⊥AB,
∴DE=EC=CD=8,
在Rt△OED中,OD2=OE2+DE2,即r2=(r﹣4)2+82,
解得,r=10,
故答案为:10;
(2)由圆周角定理得,∠DOE=2∠M,
∵∠M=∠D,
∴∠DOE=2∠D,
∴∠D=30°,
故答案为:30°.
16.【解答】解:连接OB,OD,
∵∠DOB与∠A都对,∠DOB(大于平角的角)与∠BCD都对,
∴∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,
∵∠DOB+∠DOB(大于平角的角)=360°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A=102°,
故答案为:102°
17.【解答】解:∵OD∥BC,
∴∠AOD=∠ABC=40°,
∵OA=OD,
∴∠OAD=∠ODA=70°,
∵四边形ABCD内接于⊙O,
∴∠BCD=180°﹣∠OAD=110°,
故答案为:110°.
18.【解答】解:∵圆内接四边形的对角互补,
∴∠A+∠BCD=180°,
∵∠A=60°,
∴∠BCD=120°,
∴∠DCE=180°﹣∠BCD=60°,
故答案为;圆内接四边形的对角互补,60°.
三.解答题(共6小题)
19.【解答】解:连接BD.
∵AE=AD=AB,
∴∠E=∠ADE,∠ADB=∠ABD,
∵∠E+∠EDB+∠ABD=180°,
∴2∠EDA+2∠ADB=180°,
∴∠EDA+∠ADB=90°,
∴∠BDC=∠EDB=90°,
∴BC是该圆的直径.
20.【解答】解:(1)∵△OCD是等边三角形
∴OC=OD=CD,∠OCD=∠ODC=∠COD=60°
∵OB⊥CD
∴∠COB=30°
∵∠COB=2∠CDB
∴∠CDB=15°
(2)∵sin∠OCD==
∴
∴OC=2
∴BE=OB﹣BE=2﹣3
故答案为2﹣3.
21.【解答】(Ⅰ)证明:∵=,
∴AB=BC,又∠ACB=60°,
∴△ABC是等边三角形;
(Ⅱ)∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°.
22.【解答】解:由圆周角定理得,∠A=∠1=56°,
∵四边形ABCD是圆内接四边形,
∴∠CDE=∠A=56°.
23.【解答】解:(1)∵∠BCD=120°,CA平分∠BCD,
∴∠ACD=∠ACB=60°,
由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,
∴△ABD是等边三角形;
(2)连接OB、OD,作OH⊥BD于H,
则DH=BD=,
∠BOD=2∠BAD=120°,
∴∠DOH=60°,
在Rt△ODH中,OD==,
∴⊙O的半径为.
24.【解答】解:(1)证明:∵∠ABC=90°,点M是AC的中点,
∴AM=CM=BM.
∴∠A=∠ABM.
∵四边形DEBA为⊙O的内接四边形,
∴∠ADE+∠ABM=180°,
又∵∠ADE+∠MDE=180°,
∴∠ABM=∠MDE
∴∠A=∠ABM=∠MDE.
(2)解:由(1)知∠A=∠ABM=∠MDE,
∴DE∥AB
∴△MDE∽△MAB
∴=
∵AD=2DM,∴AM=3DM
∴=
∴DE=2.
(3)证明:由(1)知∠A=∠ABM=∠MDE,
∵∠A=60°,∴∠A=∠ABM=∠MDE=60°
∴∠AMB=60°
又∵OA=OD=OE=OB
∴△AOD、△OBE都是等边三角形
∴∠ADO=∠AMB=∠OEB=60°,
∴OD∥BM,AM∥OE
∴四边形ODME是平行四边形,
又∵OD=OE
∴四边形ODME是菱形
同课章节目录
