小学数学5年级上册第七单元同步练习题(含答案)
文档属性
| 名称 | 小学数学5年级上册第七单元同步练习题(含答案) | 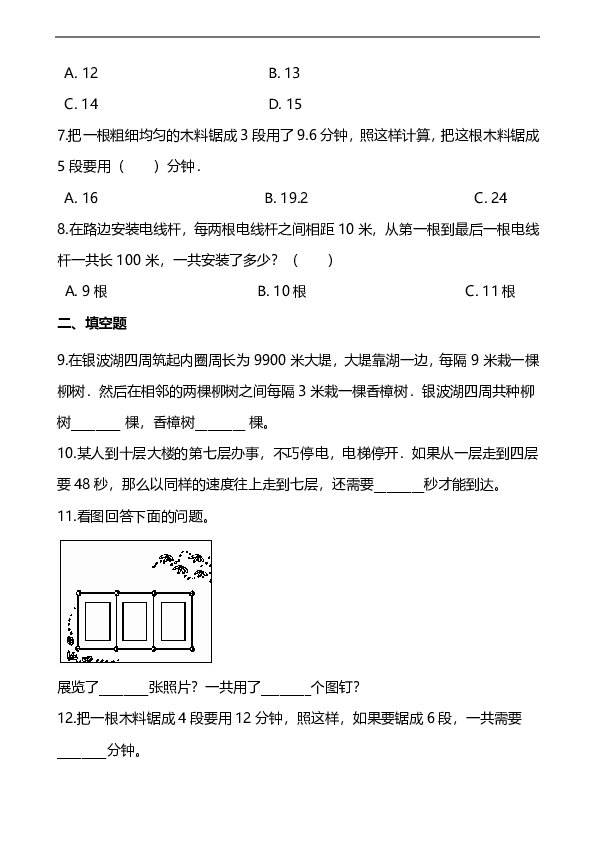 | |
| 格式 | zip | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-04 17:45:47 | ||
图片预览



文档简介
第七单元 同步练习
一、单选题
1.一座 6 层的楼房.一层到二层有台阶 22 级,第二层到第六层每相邻楼层有 20
级台阶,这座楼房一共有台阶( )
A. 112 级 B. 102 级
C. 122 级 D. 132 级
2.要在 20 米长的阳台上放 11 盆花,不管怎样放,( )花之间的距离不超过 2
米。
A. 刚好 2 盆 B. 至少有 2 盆
C. 至少有 3 盆 D. 刚好有 3 盆
3.小区花园是一个长 60 米,宽 40 米的长方形,现在要在花园的四周栽树,四
个角都要栽,每相邻两棵间隔 5 米。一共要栽( )棵。
A. 20 B. 36
C. 40 D. 44
4.把 4 米长的木棒平均截成 5 段要 5 分钟,每截一段要( )分钟.
A. 1 B.
C. D.
5.若将 28 棵树围成一个正方形,那么正方形平均每边应栽( )棵树
A. 5 B. 6
C. 7 D. 8
6.一辆电车从起点到终点一共要行 36 千米,如果每隔 3 千米停靠站一次,那么
从起点到终点,一共要停靠( )次(起点不算).
A. 12 B. 13
C. 14 D. 15
7.把一根粗细均匀的木料锯成 3 段用了 9.6 分钟,照这样计算,把这根木料锯成
5 段要用( )分钟.
A. 16 B. 19.2 C. 24
8.在路边安装电线杆,每两根电线杆之间相距 10 米,从第一根到最后一根电线
杆一共长 100 米,一共安装了多少?( )
A. 9 根 B. 10 根 C. 11 根
二、填空题
9.在银波湖四周筑起内圈周长为 9900 米大堤,大堤靠湖一边,每隔 9 米栽一棵
柳树.然后在相邻的两棵柳树之间每隔 3 米栽一棵香樟树.银波湖四周共种柳
树________ 棵,香樟树________ 棵。
10.某人到十层大楼的第七层办事,不巧停电,电梯停开.如果从一层走到四层
要 48 秒,那么以同样的速度往上走到七层,还需要________秒才能到达。
11.看图回答下面的问题。
展览了________张照片?一共用了________个图钉?
12.把一根木料锯成 4 段要用 12 分钟,照这样,如果要锯成 6 段,一共需要
________分钟。
13.一根钢管,要把它锯成长度相等的 6 段,每锯一次要 8 分钟.锯完这根钢管
一共需要________分钟。
三、解答题。
14.幸福小建了一个正三角形花坛,花坛每边都摆了 15 盆花(每个顶点都有一
盆),一共摆了多少盆花?
15.从甲地到乙地原来每隔 45 米要装一根电线杆,加上两端的两根,一共有 53
根电线杆,现在改成每隔 60 米装一根电线杆,除两端的两根不需要移动外,中
途还有多少根不必移动?
16.公路上有一排电线杆,共 25 根,每相邻两根间的距离原来都是 45 米,现在
要改成 60 米,可以有几根不需要移动?
四、综合题
17.学校举行运动会,要在操场四周插上彩旗。操场周长 300 米,按下图方式每
隔一米插一面彩旗。
(1)一共需要多少面彩旗?
(2)第 53 面彩旗是什么颜色?
(3)布置完整个操场,红、黄、绿色彩旗各需要多少面?
五、应用题
18.小红和小芳同住一幢高层建筑,小红家住在 5 楼,小芳家住在 20 楼,两人
都从一楼乘电梯上楼,如果两个电梯速度相同,小红从 1 楼到 5 楼用了 分钟,
那么小芳从 1 楼到 20 楼要多少分钟?
19.工人叔叔在公路的一侧从头到尾每隔 80 米立一根电线杆,刚好立了 9 根.你
知道这段公路长多少米吗?
20.亮亮沿一条直线在桌子上等距离地摆了 5 颗棋子,已知第 1 颗到第 5 颗的距
离是 8 厘米,每两颗棋子的距离是多少?
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】第二层到第六层共有 4 层台阶,共 20×4=80(级),80+
22=102(级),选 B.
2.【答案】B
【解析】【解答】11 盆花之间有 11-1=10 个间隔,每个间隔平均是 20÷10=2
(米),把这 10 个间隔看作 10 个抽屉,把 11 盆花放在 10 抽屉里,总能保证
至少有一个抽屉里有两盆花,即至少有 2 盆花的距离不超过 2 米.
故答案为:B。
【分析】本题考点:抽屉原理;植树问题。
此题问题原型属于抽屉原理,关键是根据 11 盆花求出间隔数是 10,即得出 10
个抽屉,再利用抽屉原理即可解答。
根据题干分析可得,11 盆花一共有 11-1=10 个间隔,根据抽屉原理,从最差
情况考虑:使每个间隔的长度尽量的平均,则每个间隔的长度最少是 20÷10=2
米,由此即可解答。
3.【答案】C
【解析】【解答】解:(60+40)×2÷5
=200÷5
=40(棵)
故答案为:C【分析】由于是封闭的图形,且长和宽的长度都是 5 的倍数,那么
可以直接用长方形的周长除以每相邻两棵间隔的长度求出一共要栽的棵数即可.
4.【答案】D
【解析】【解答】解:5÷4= (分钟),
答:每截一段需要 分钟.
故选:D.
【分析】把木棒平均锯成 5 段,需要锯 5﹣1=4 次,用总时间除以锯的次数即
可.
5.【答案】D
【解析】【解答】(28+4)÷4
=32÷4
=8(棵)
故答案为:D.
【分析】根据题意可知,用树围成一个正方形,正方形 4 个顶点处的树会被计
算两次,所以先将树的棵数加上 4,然后平均分,据此解答.
6.【答案】A
【解析】【解答】解:36÷3=12(次),
答:一共要停靠 12 次.
故选:A.
【分析】起点不算,那么停靠的次数=间隔数,由此求出 36 千米里面有几个 3
千米的间隔,即可解答问题.
7.【答案】B
【解析】【解答】解:9.6÷(3﹣1)×(5﹣1),
=9.6÷2×4,
=19.2(分钟),
答:锯成 5 段需要 19.2 分钟.
故选:B.
【分析】把一根木头锯成 3 段,那么就是要锯 2 次,才会有 3 段,那么每锯一
次所要花费的时间是:9.6÷2=4.8 分钟;现在锯成 5 段,就是要锯 4 次那么总
共需要时间是:4×4.8=19.2 分钟.
8.【答案】C
【解析】【解答】解:一共安装电线杆:
100÷10+1
=10+1
=11(根)
答:一共安装了 11 根电线杆.
故选:C.
【分析】每两根电线杆之间相距 10 米,从第一根到最后一根电线杆共长 100
米,也就是把 100 米平均分成 10 米长的若干小段,电线杆安在各分点上,因
为两端都要安装电线杆,电线杆的数量等于段数加 1.
二、填空题
9.【答案】1100;2200
【解析】【解答】解:柳树有:9900÷9=1100(棵),
香樟树有:(9÷3﹣1)×1100,
=2×1100,
=2200(棵),
答:银波湖四周共种柳树 1100 棵,香樟树 2200 棵.
故答案为:1100;2200.
【分析】①围圆湖周边植树时,植树棵数=间隔数,由此可以求得柳树的棵数;
②根据题干,柳树之间的间隔长度是 9 米,每隔 3 米栽一棵香樟树,有 9÷3=3
个小间隔,因为两端都是柳树,所以每两棵柳树之间都有 3﹣1=2 棵香樟树,
那么香樟树的棵数为:间隔数×2;据此解答.
10.【答案】48
【解析】【解答】解:“从一层走到四层”,实际上是爬了 3 层楼梯,共需要
48 秒,
从四楼走到七楼又需要爬 7﹣4=3 层楼梯,所以还需要 48 秒,
故答案为:48.
【分析】“从一层走到四层”,实际上是爬了 3 层楼梯,共需要 48 秒,从四楼
走到七楼又需要爬 7﹣4=3 层楼梯,所以还需要 48 秒,由此即可解答.
11.【答案】3;8
【解析】【解答】
观察图形可知,图中共有 3 张照片
一共用的图钉的个数为:
(3+1)×2
=4×2
=8(个)
故答案为:3;8.
【分析】解答本题的关键是明确如果在非封闭线路的两端都要植树,那么:株
数=段数+1.
12.【答案】20
【解析】【解答】解:12÷(4-1)=4(分钟);
4×(6-1)
=4×5
=20(分钟)
故答案为:20
【分析】锯成 4 段只需要锯 3 次,锯成 6 段需要锯 5 次,用 12 除以 3 即可求
出锯一次的时间,然后乘 5 即可求出锯成 6 段需要的时间.
13.【答案】40
【解析】【解答】解:(6﹣1)×8
=5×8
=40(分钟)
答:锯完这根钢管一共需要 40 分钟.
故答案为:40.
【分析】首先要明确把它锯成 6 段需要锯 6﹣1=5 次,然后根据需要的时间=
锯的次数×锯一次需要的时间解答.
三、解答题
14.【答案】解:15×3 3=42(盆)答:一共摆了 42 盆花。
【解析】【分析】:根据题意,在正三角形的三条边上摆花盆,三个顶点都放,
那么在数每一边的时候,会多数 3 盆,用每边摆 15 盆乘上边数 3,再减去顶点
的个数 3 盆即可。
15.【答案】解:从甲地到乙地一共长:45×(53﹣1)=2340(米),
45 和 60 的最小公倍数是:180;
2340÷180﹣1,
=12(根);
答:中间还有 12 跟不必移动.
【解析】【分析】共有(53﹣1)=52 个间隔,总长 45×52=2340 米,45,60
的最小公倍数 180,2340÷180=13 个,
由于 2340 也是 180 的倍数,所以中间还有 13﹣1=12 根不必移动.
16.【答案】解:公路长度:45×(25﹣1)=1080(米),
显然所有 45 和 60 的最小公倍数不用移动,
45 和 60 的最小公倍数为:180,
不用移动根数:1080÷180=6(根),
6+1=7(根),后面加的 1 根就是起点(端点)的一根,肯定是不动的.
答:可以有 7 根不需要移动.
【解析】【分析】根据题意明白不需要移动电线杆数就是 45 和 60 的公倍数是
哪些点上的电线杆不移动,起点的一根肯定是不动的,那就要先求出公路总长,
再求出两种间距米数的最小公倍数,最后算一算公路总长里有几个最小公倍
数.最后加上起点那根.
四、综合题
17.【答案】(1)解:300÷1=300(面)
答:一共需要 300 面彩旗。
(2)解:由彩旗排列顺序可得:5 面彩旗是一个周期,这 5 面彩旗排列顺序是
红色、黄色、绿色、黄色、红色,53÷5=10(个)……3(面),余数 3 是下一
个周期的第 3 面,第 3 面是绿色的。
答:第 53 面彩旗是绿颜色。
(3)解:300÷5=60(个),红色:2×60=120(面),黄色:2×60=120(面);
绿色:1×60=60(面)。
答:红色彩旗 120 面,黄色彩旗 120 面,绿色彩旗 60 面。
【解析】【分析】对于(1)题,封闭线路上的植树问题的数量关系:株数=全
长÷株距,代入数据计算即可;对于(2)题,首先明确彩旗排列顺序:红色、
黄色、绿色、黄色、红色,即 5 面彩旗是一个周期,再用 53 除以 5 根据求得的
余数即可解答;对于(3)题,首先明确 5 面彩旗是一个周期,一个周期中红旗
是 2 面、黄旗是 2 面,绿旗是 1 面,再用彩旗的总数量 300 除以一个周期中彩
旗的面数 5,求出有几个周期,再用一个周期中每种颜色旗乘周期个数即可解答。
五、应用题
18.【答案】解: ÷(5﹣1)×(20﹣1)
= ÷4×19
= ×19
= (分钟)
答:小芳从 1 楼到 20 楼要 分钟.
【解析】【分析】小红从 1 楼到 5 楼用了 分钟,一共上了 4 层,那么上一层
需要的时间是 ÷4 分钟;小芳从 1 楼到 20 楼需要上 20﹣1=19 层,再用上每
层的时间乘上上的层数即可求解.
19.【答案】解:(9﹣1)×80
=8×80
=640(米),
答:这条路长 640 米.
【解析】【分析】两端都要栽时,间隔数=电线杆的根数﹣1,所以这里间隔数
是 9﹣1=8,再乘 80 就是这条路的长度.
20.【答案】解:8÷(5﹣1)
=8÷4
=2(厘米)
答:每两颗棋子的距离是 2 厘米.
【解析】【分析】由题意,在桌子上等距离地摆了 5 颗棋子,则用 5﹣1 可求出
间隔数,再用总距离 8 厘米除以间隔数即得间距,即每两颗棋子的距离是多少;
据此解答.
