5.1.1 平行四边形的性质同步练习
图片预览


文档简介
5.1 平行四边形的性质
第1课时平行四边形的定义及性质1、2
自主预习
1.平行四边形的定义:两组对边分别_______________四边形叫做平行四边形。
2.平行四边形的对称性:平行四边形是__________对称图形,__________的交点是它的对称中心。
3.平行四边形的性质定理1:平行四边形的对边________________。
4.平行四边形的性质定理2:平行四边形的对角________________。
课堂巩固
知识点:平行四边形的性质
1.如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
A.4个 B.6个 C.8个 D.9个
2.如图,在 ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则 ABCD的周长是( )
A. 20 cm B. 21 cm C. 22 cm D. 23 cm
1题图 2题图 3题图 4题图
3.(2018衡州)如图,在 ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65o D.75°
4.如图,在 ABCD中,∠A=120°,则∠C=___________。
5.如图,在 ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=_______cm。
6.如图, ABCD与 DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为__________。
5题图 6题图 7题图 8题图
7.如图,C为AB的中点,四边形ACDE为平行四边形,BE与CD相交于点F,求证:EF=BF。
8.如图,在 ABCD中,BD⊥AD,∠A=45,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O 。
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长。
课后提升
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6 cm B.12 cm C.4 cm D.8 cm
2.已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100o B.160° C.80° D.60o
1题图 3题图 4题图
3.如图,在 ABCD中,AB=3,AD=2,∠B=150°,则平行四边形ABCD的面积为( )
A.2 B.3 C. D.6
4.如图,已知点E,F是平行四边形ABCD对角线上的两点,请添加一个条件____________________,使△ABE≌△CDF(只填一个即可)。
5.平行四边形的一条对角线与一边垂直,且此对角线为另一边的一半,则此平行四边形两邻角的度数之比为_____________。
6.如图,在平面直角坐标系中, ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是_______________。
6题图 7题图
7.在 ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH。
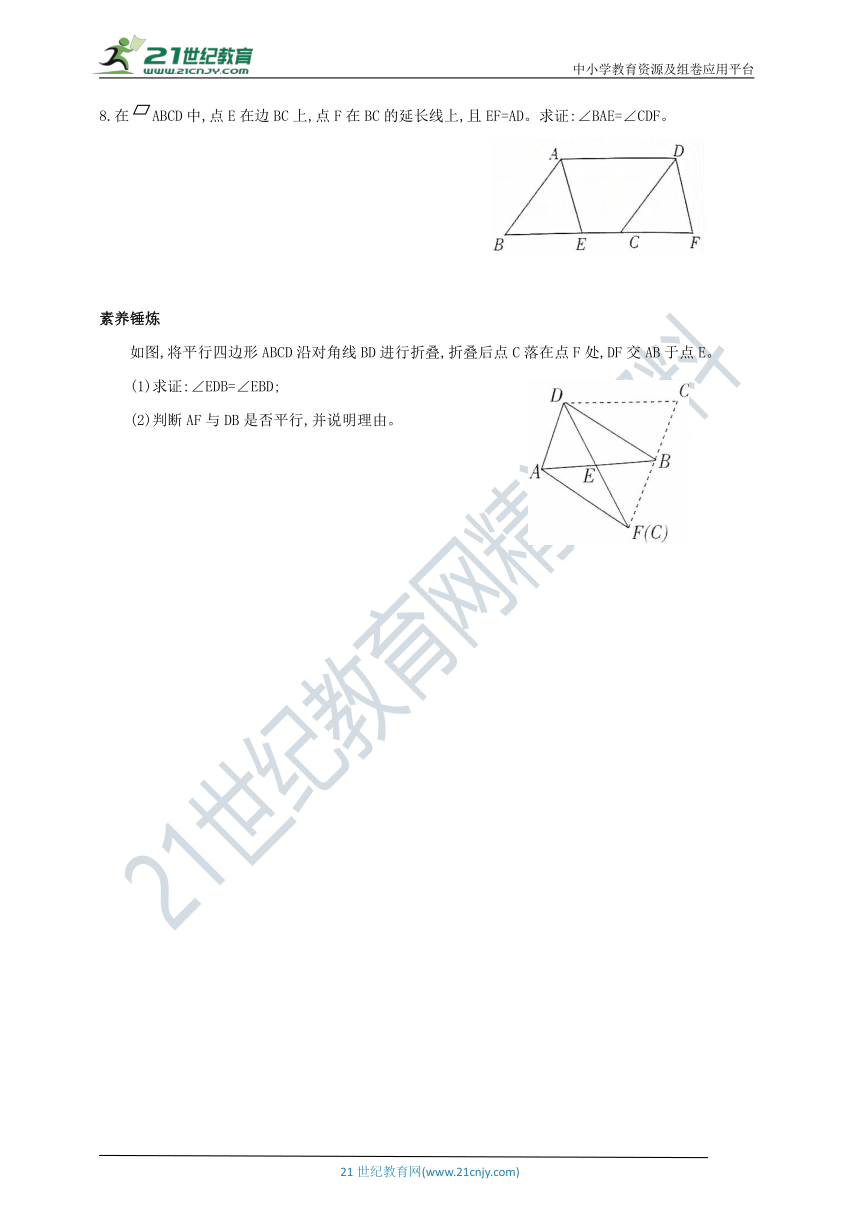
8.在 ABCD中,点E在边BC上,点F在BC的延长线上,且EF=AD。求证:∠BAE=∠CDF。
素养锤炼
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E。
(1)求证:∠EDB=∠EBD;
(2)判断AF与DB是否平行,并说明理由。
参考答案及解析
自主预习
1.平行 2.中心 两条对角线 3.相等 4.相等
课堂巩固
1.D 2.C 3.A 4.120o 5. 2 6. 25o
7.证明:∵四边形ACDE为平行四边形,∴ED=AC,ED∥AC,∴∠D=∠FCB,∠DEF=∠B,∵C为AB的中点,∴AC=BC,∴ED=BC。∵∠D=∠FCB,∠DEF=∠B,∴△DEF≌△CBF,∴EF=BF。
8.(1)证明:∵四边形ABCD是平行四边形,∴DC=AB,DC∥AB
DF=∠OB DOF=∠BO,∴∠ODF=∠OBE,在△ODF和△OBE中:∠ODF=∠OBE;∠DOF=∠BOE;DF=BE。
∴△ODF≌△OBE(AAS)∴BO =DO
(2)解:∵BD⊥AD,∴∠ADB=90o,∵∠A=45o,∴∠DAB=∠A=45o,∴△ODG是等腰直角三角形,
∵EF⊥AB,∴∠G=∠A=45o,∴AB∥CD,EF⊥AB,∴DF⊥OG,∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)∴ OE=OF,∴GF =OF=OE,即2FG=EF,∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,∴在等腰Rt△ADB中,DB=2DO=2=AD,∴AD=2.
课后提升
1.D 2.C 3.B
4.答案不唯一,如AE=CF 5. 1:5 或5:1 6. (7,3)
7.证明:∵ 四边形ABCD是平行四边形,∴AB∥CD,∴∠E=∠ECD,∵EC平分∠BCD,
∴∠BCE=∠ECD。∴∠E=∠BCE。∴BC=BE。∵BH⊥EC,∴CH=EH。
8.证明:∵四边形ABCD是平行四边形, ∴AB=CD,AD=BC,AB∥CD∴∠ABE=∠DCF,
又∵EF=AD, ∴BC=EF ∴BE=CF
在△ABE和△DCF中: AB=DC、∠B=∠DCF,EB=CF,
∴△BAE≌△CDF(SAS)∴∠BAE=∠CDF
素养锤炼
(1)证明:由折叠可知:∠CDB=∠EDB。
∵四边形ABCD是平行四边形,∴DC∥AB∴∠CDB=∠EBD,∴∠EDB=∠EBD;
(2)解:AF∥DB.理由如下:
∵∠EDB=∠EBD,∴DE=BE,由折叠可知:DC=DF,
∵四边形ABCD是平行四边形 ∴DC=AB,∴AB=DF,∵∠EDB=∠EBD,∴DE=BE.
∴AB-EB=DF-DE, ∴AE=EF,∴∠EAF=∠EFA。
在△BED中,∠EDB+∠EBD+∠DEB=180°即2∠EDB+∠DEB=180°。
同理,在△AEF中,2∠EFA+∠AEF=180o∵∠DEB=∠AEF,∴∠EDB=∠EFA。
∴ AF∥DB.
第1课时平行四边形的定义及性质1、2
自主预习
1.平行四边形的定义:两组对边分别_______________四边形叫做平行四边形。
2.平行四边形的对称性:平行四边形是__________对称图形,__________的交点是它的对称中心。
3.平行四边形的性质定理1:平行四边形的对边________________。
4.平行四边形的性质定理2:平行四边形的对角________________。
课堂巩固
知识点:平行四边形的性质
1.如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
A.4个 B.6个 C.8个 D.9个
2.如图,在 ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则 ABCD的周长是( )
A. 20 cm B. 21 cm C. 22 cm D. 23 cm
1题图 2题图 3题图 4题图
3.(2018衡州)如图,在 ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65o D.75°
4.如图,在 ABCD中,∠A=120°,则∠C=___________。
5.如图,在 ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=_______cm。
6.如图, ABCD与 DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为__________。
5题图 6题图 7题图 8题图
7.如图,C为AB的中点,四边形ACDE为平行四边形,BE与CD相交于点F,求证:EF=BF。
8.如图,在 ABCD中,BD⊥AD,∠A=45,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O 。
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长。
课后提升
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6 cm B.12 cm C.4 cm D.8 cm
2.已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100o B.160° C.80° D.60o
1题图 3题图 4题图
3.如图,在 ABCD中,AB=3,AD=2,∠B=150°,则平行四边形ABCD的面积为( )
A.2 B.3 C. D.6
4.如图,已知点E,F是平行四边形ABCD对角线上的两点,请添加一个条件____________________,使△ABE≌△CDF(只填一个即可)。
5.平行四边形的一条对角线与一边垂直,且此对角线为另一边的一半,则此平行四边形两邻角的度数之比为_____________。
6.如图,在平面直角坐标系中, ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是_______________。
6题图 7题图
7.在 ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH。
8.在 ABCD中,点E在边BC上,点F在BC的延长线上,且EF=AD。求证:∠BAE=∠CDF。
素养锤炼
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E。
(1)求证:∠EDB=∠EBD;
(2)判断AF与DB是否平行,并说明理由。
参考答案及解析
自主预习
1.平行 2.中心 两条对角线 3.相等 4.相等
课堂巩固
1.D 2.C 3.A 4.120o 5. 2 6. 25o
7.证明:∵四边形ACDE为平行四边形,∴ED=AC,ED∥AC,∴∠D=∠FCB,∠DEF=∠B,∵C为AB的中点,∴AC=BC,∴ED=BC。∵∠D=∠FCB,∠DEF=∠B,∴△DEF≌△CBF,∴EF=BF。
8.(1)证明:∵四边形ABCD是平行四边形,∴DC=AB,DC∥AB
DF=∠OB DOF=∠BO,∴∠ODF=∠OBE,在△ODF和△OBE中:∠ODF=∠OBE;∠DOF=∠BOE;DF=BE。
∴△ODF≌△OBE(AAS)∴BO =DO
(2)解:∵BD⊥AD,∴∠ADB=90o,∵∠A=45o,∴∠DAB=∠A=45o,∴△ODG是等腰直角三角形,
∵EF⊥AB,∴∠G=∠A=45o,∴AB∥CD,EF⊥AB,∴DF⊥OG,∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)∴ OE=OF,∴GF =OF=OE,即2FG=EF,∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,∴在等腰Rt△ADB中,DB=2DO=2=AD,∴AD=2.
课后提升
1.D 2.C 3.B
4.答案不唯一,如AE=CF 5. 1:5 或5:1 6. (7,3)
7.证明:∵ 四边形ABCD是平行四边形,∴AB∥CD,∴∠E=∠ECD,∵EC平分∠BCD,
∴∠BCE=∠ECD。∴∠E=∠BCE。∴BC=BE。∵BH⊥EC,∴CH=EH。
8.证明:∵四边形ABCD是平行四边形, ∴AB=CD,AD=BC,AB∥CD∴∠ABE=∠DCF,
又∵EF=AD, ∴BC=EF ∴BE=CF
在△ABE和△DCF中: AB=DC、∠B=∠DCF,EB=CF,
∴△BAE≌△CDF(SAS)∴∠BAE=∠CDF
素养锤炼
(1)证明:由折叠可知:∠CDB=∠EDB。
∵四边形ABCD是平行四边形,∴DC∥AB∴∠CDB=∠EBD,∴∠EDB=∠EBD;
(2)解:AF∥DB.理由如下:
∵∠EDB=∠EBD,∴DE=BE,由折叠可知:DC=DF,
∵四边形ABCD是平行四边形 ∴DC=AB,∴AB=DF,∵∠EDB=∠EBD,∴DE=BE.
∴AB-EB=DF-DE, ∴AE=EF,∴∠EAF=∠EFA。
在△BED中,∠EDB+∠EBD+∠DEB=180°即2∠EDB+∠DEB=180°。
同理,在△AEF中,2∠EFA+∠AEF=180o∵∠DEB=∠AEF,∴∠EDB=∠EFA。
∴ AF∥DB.
