沪科版初中数九年级上册第23章解直角三角形专题训练(含精讲解析)
文档属性
| 名称 | 沪科版初中数九年级上册第23章解直角三角形专题训练(含精讲解析) |  | |
| 格式 | zip | ||
| 文件大小 | 204.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-07 12:49:52 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
第23章解直角三角形专题训练(含精讲解析)
一、单选题(共10题;共30分)
1.如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( ??)
A.?1.25???????????????????????B.?0.8???????????????????????????C.?0.6???????????????????????????D.?0.625
2.cos45°的值是(?????)
A.???????????????????????????????B.?????????????????????????C.?????????????????????????????????????????D.?1
3.在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 , 则∠A的正切值( )
A.?缩小为原来的????????????????B.?扩大为原来的4倍????????????????
C.?缩小为原来的????????????????D.?没有变化
4.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A.?25+75??????????B.?50+50???????????C.?75+75???????????????D.?50+100
5.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠ABP=( )
A.? ??????B.?2 ?C.? ?D.?
6.(2015?威海)如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.?5÷tan26°=? ? ? ????B.?5÷sin26°=????????C.?5×cos26°=? ? ? ???????D.?5×tan26°
7.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A、A′的余弦值的关系为( )
A.?cosA=cosA′ B.?cosA=3cosA′ C.?3cosA=cosA′ D.?不能确定
8.如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为(?? )
A.???????????????????B.???????????????????????C.????????????????????????????????D.?
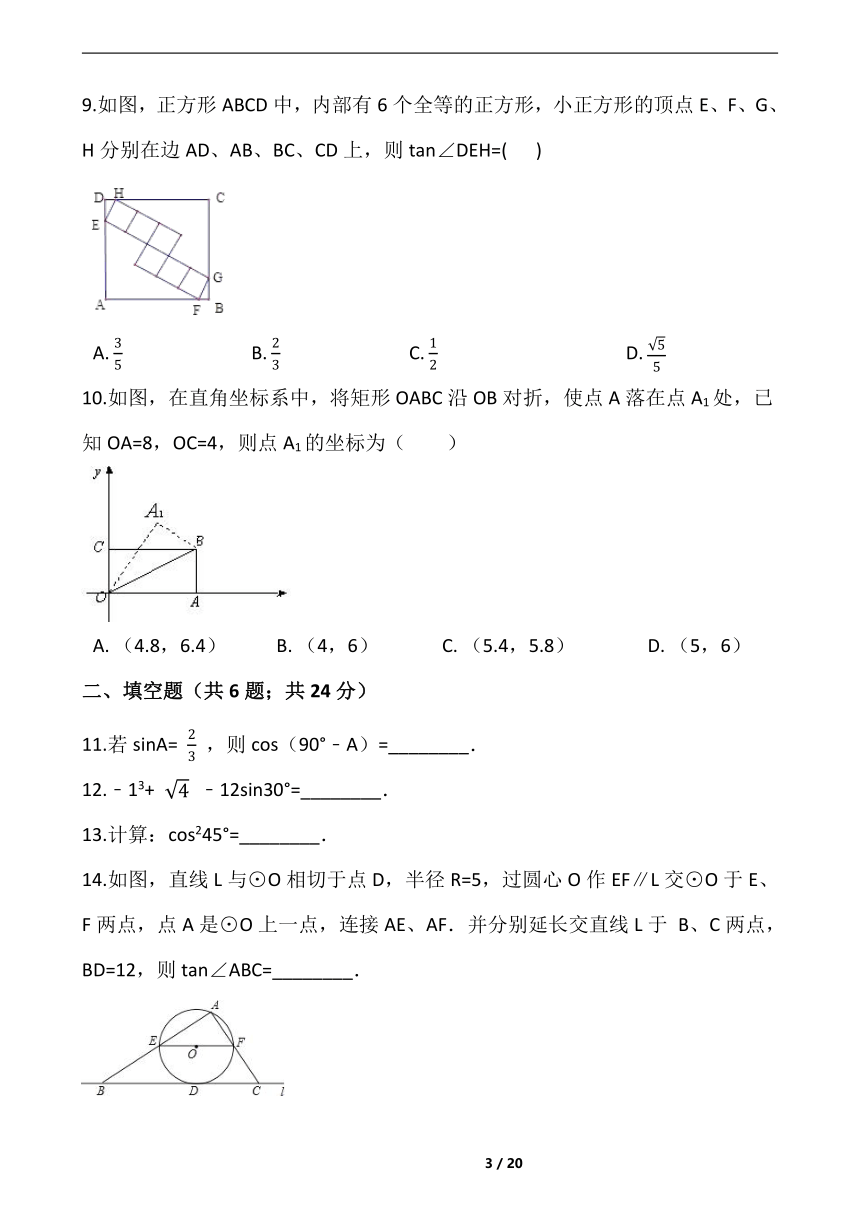
9.如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别在边AD、AB、BC、CD上,则tan∠DEH=( ????)
A.?????????????????????????????B.?????????????????????????????C.??????????????????????????????????????????D.?
10.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
A.?(4.8,6.4)???????????B.?(4,6)??????????????C.?(5.4,5.8)????????????????D.?(5,6)
二、填空题(共6题;共24分)
11.若sinA= ,则cos(90°﹣A)=________.
12.﹣13+ ﹣12sin30°=________.
13.计算:cos245°=________.
14.如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=________.
15.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ?.下列结论:
①△ADE∽△ACD;????? ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8;? ④0
其中正确的结论是________.(把你认为正确结论的序号都填上)
16.勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为________.
三、计算题(共4题;共31分)
17.计算:(π﹣2016)0﹣2tan45°+( )﹣2 .
18.先化简,再求值:( ﹣ )÷ ,其中x=tan45°+2cos60°.
19.计算:
20.计算:
(1) ﹣3tan30°﹣( )﹣2﹣4( ﹣2)2
(2)6tan230°﹣ sin60°﹣cos45°.
四、解答题(共4题;共36分)
21.如图,小明在操场上放风筝,已知风筝线AB长100? 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
22.如图,图①是某电脑液晶显示器的侧面图,显示屏AO可以绕点O旋转一定的角度.研究表明:显示屏顶端A与底座B的连线AB与水平线BC垂直时(如图②),人观看屏幕最舒适.此时测得∠BAO=15°,AO=30cm,∠OBC=45°,求AB的长度.(结果精确到1cm)(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, ≈1.414)
23.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
24.(2017?宿迁)如图所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
五、综合题(共2题;共29分)
25.如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH= ,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
26.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH?EA;
(3)若⊙O的半径为 ,sinA= ,求BH的长.
答案解析部分
一、单选题
1.【答案】B
【考点】等腰三角形的性质,锐角三角函数的定义
【解析】【解答】解:作AD⊥BC于D,如图,
∵AB=AC=5,
∴BD=CD= BC= ×8=4,
在Rt△ABD中,cosB= = .
故答案为:B.
【分析】作AD⊥BC于D根据等腰三角形的三线合一得出BD=CD,在Rt△ABD中根据余弦函数的定义得出cosB的值。
2.【答案】C
【考点】特殊角的三角函数值
【解析】
【分析】根据特殊角的三角函数值直接解答即可.
【解答】cos45°=.
故选C.
【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要熟练掌握.
3.【答案】D
【考点】锐角三角函数的定义
【解析】【解答】解:∵在Rt△ABC中,如果每个边都缩小为原来的 ,
∴锐角A的对边与邻边的比值不变,
∴锐角A的正切值不变.
故选D.
【分析】根据题意得到锐角A的对边与邻边的比值不变,然后根据正切的定义可判断锐角A的正切值不变.
4.【答案】D
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:设AE=xm,在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面50m,
∴OE=50m,
∴OP′=OP=PE+OE=x+50,
∵∠P′AE=60°,
∴P′E=tan60°?AE=x,
∴OP′=P′E﹣OE=x﹣50,
∴x+50=x﹣50,
解得:x=50(+1)(m),
∴PO=PE+OE=50(+1+50=50+100(m),
即飞艇离开湖面的高度是(50+100)m;
故选:D.
【分析】设AE=x,则PE=AE=x,根据山顶A处高出水面50m,得出OE=50,OP′=x+50,根据∠P′AE=60°,得出P′E=x,从而列出方程,求出x的值即可.
5.【答案】A
【考点】锐角三角函数的定义,解直角三角形的应用﹣方向角问题
【解析】【分析】根据题意作出图形后知道北偏东30°与北偏西60°成直角,利用正切的定义求值即可.
【解答】∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°? BP=60×=40
∴tan∠ABP===
故选A.
【点评】本题考查了解直角三角形的应用,解题的关键是根据实际问题整理出直角三角形并利用正切的定义求值.
6.【答案】D
【考点】计算器—三角函数
【解析】【解答】解:由tanB=,得
AC=BC?tanB=5×tan26.
故选:D.
【分析】根据正切函数的定义,可得tanB=?,根据计算器的应用,可得答案.
7.【答案】A
【考点】锐角三角函数的增减性
【解析】【解答】解:根据锐角三角函数的概念,知
把Rt△ABC各边的长度都扩大3倍,那么它们的余弦值不变.
故选A.
【分析】锐角三角函数即为直角三角形中有关边的比值.
8.【答案】B
【考点】坐标与图形性质,圆周角定理,解直角三角形
【解析】【解答】解:连接EC,
∵∠COE=90°,
∴EC是⊙A的直径,
∵C(0,6),E(﹣8,0),O(0,0),
∴OC=6,OE=8,
由勾股定理得:EC=10,
∵∠OBC=∠OEC,
∴cos∠OBC=cos∠OEC= = = .
故答案为:B.
【分析】∠OBC不处在直角三角形中,因此需连直径转化∠OBC为∠OEC,且又处于直角三角形中,再利用余弦定义可求出.
9.【答案】A
【考点】勾股定理,相似三角形的性质,相似三角形的判定,锐角三角函数的定义
【解析】【解答】∵正方形ABCD的边长为10a,
∴∠A=∠B=90° ,AB=10a,
过点G作GP⊥ AD,垂足为P,则∠DPG=∠APG.
∴四边形APGB是矩形,
∴∠PGF+∠BGF=90°,PG=AB=10a,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠EGP+∠PGF=90°,
∴∠EGP=∠BGF
∴△BGF∽△PGE,
∴,
∴GB=AP=2a,
同理DE=2a,
∴PE=AD-AP-DE=6a,
∴EG==2a,
∴小正方形的边长为a,
∴DH==a
∴tan∠DEH==
故本题正确选项为A。
【分析】过点G作GP⊥ AD,垂足为P,可以得到△BGF∽△PGE,再根据相似三角形对应边成比例的性质列式求解即可得到DE和BG的长,根据勾股定理可求出EG的长,从而求出DH的长,再根据三角函数的定义得出答案。
10.【答案】A
【考点】翻折变换(折叠问题),解直角三角形
【解析】
【分析】设出A1点的坐标,先根据翻折变换的性质得出△A1BD的面积,作A1E⊥x轴于E,交DE于F,根据BC∥x轴可知A1E⊥BC,再由(1)中BD的值及三角形的面积公式可求出A1F的长,B点坐标,用待定是法求出过O、D两点的一次函数的解析式,把A1点的坐代入函数解析式即可.
【解答】∵BC∥AO,
∴∠BOA=∠OBC,
根据翻折不变性得,
∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2 ,
解得x=5.
∴BD=5,
∴S△BDO=×5×4=10;
设A1(a,4+b),作A1E⊥x轴于E,交DE于F,如下图所示:
∵BC∥x轴,
∴A1E⊥BC,
∵S△OAB=OA?AB=×8×4=16,S△BDO=10.
∴S△A1BD=BD?A1F=×5A1F=6,
解得A1F=,
∴A点的纵坐标为?,
∵BD=5,B(8,4)
∴D点坐标为(3,4),
∴过OC两点直线解析式为y=x,
把A点的坐标(a,)代入得,=a,
解得a=,
∴A点的坐标为(?,).即(4.8,6.4)
故选A.
二、填空题
11.【答案】
【考点】互余两角三角函数的关系
【解析】【解答】解:∵∠A与∠90°﹣A互余,
∴cos(90°﹣A)=sinA= .
故答案为 .
【分析】根据一个角的正弦值等于它的余角的余弦值即可求解.
12.【答案】-5
【考点】特殊角的三角函数值
【解析】【解答】解:原式=﹣1+2﹣12× =﹣1+2﹣6=﹣5,
故答案为:﹣5.
【分析】先依据有理数的乘方法则、算术平方根的性质、特殊锐角三角函数值进行化简,最后,在进行计算即可.
13.【答案】
【考点】特殊角的三角函数值
【解析】【解答】解:原式=()2== .
【分析】运用特殊角三角函数值计算.
14.【答案】
【考点】切线的性质,解直角三角形
【解析】【解答】解:连接OD,则OD⊥BD,
过E作EH⊥BC,垂足为H,如图,
∴EH∥OD,
∵EF∥BC,OE=OD,
∴四边形EODH是正方形,
∴EH=HD=OD=5,
又∵BD=12,
∴BH=7,
在Rt△BEH中,tan∠ABC= = .
【分析】由EF∥BC,OE=OD,得到四边形EODH是正方形,根据正方形的性质,得到四边相等,求出在Rt△BEH中,tan∠ABC.
15.【答案】①②④
【考点】二次函数的最值,全等三角形的判定与性质,相似三角形的判定与性质,解直角三角形的应用
【解析】【解答】作AH⊥BC于H , 如图,
∵AB=AC ,
∴∠B=∠C=α , BH=CH ,
而∠ADE=∠B=α ,
∴∠ADE=∠C ,
而∠DAE=∠CAD ,
∴△ADE∽△ACD , 所以①正确;
在Rt△ABH中,cosB= ,
∴BH=10× ?=8,
∴BC=2BH=16,
当BD=6,则CD=10,
∵∠ADC=∠B+∠BAD ,
而∠ADE=∠B=α ,
∴∠EDC=∠BAD ,
在△ABD与△DCE中
,
∴△ABD≌△DCE , 所以②正确;
∵∠B=∠C , ∠BAD=∠CDE ,
∴△ABD∽△DCE ,
△DCE为直角三角形,当∠DEC=90°,则∠ADB=90°,BD为8;
当∠EDC=90°,则∠BAD=90°,BD= ,所以③错误;
设BD=x , 则CD=16-x ,
由△ABD∽△DCE得 ?,即 ,
∴CE=- ?,
∴CE的最大值为6.4,
∴0<CE≤6.4,所以④正确.
故答案为:①②④.
【分析】①利用三个角相等的两个三角形相似来证明;②利用角相等,将所给的余弦函数变为∠B的余弦函数,从而利用角边角证得△ABD≌△DCE;③利用三角形相似对应边成比例,再结合所求及所给线段的长度求得BD的长度;④由三角形相似对应边成比例用BD的表示出CE的长度,再利用二次函数的图像特征计算出CE的取值范围.
16.【答案】(7 +6,0)
【考点】全等三角形的判定与性质,等边三角形的判定与性质,锐角三角函数的定义
【解析】【解答】延长BA交QR于点M , 连接AR , AP ,
在△ABC与△GFC中,
?
?
?
????
又∵ ?
?
?
?
?
∴△QHG是等边三角形.
?
则 ?
在 中, ??
在 中, ?
? ?
?
?
∴点P的坐标为
故答案为:
【分析】 延长BA交QR于点M , 连接AR , AP , 先利用SAS判断出△ABC≌△GFC,然后根据全等三角形的性质得出∠ C G F = ∠ B A C = 30 ? , 进一步得出HGQ=60? , 然后周角的定义得出BAC+∠DAH=180,再根据二直线平行同旁内角互补得出RHA+∠DAH=180? , 再根据同角的补角相等得出RHA=∠BAC=30? , 进而判断出△QHG是等边三角形.根据余弦的定义得出AC的长,从而根据正方形的性质得出 Q H = H A = H G = A C = 2? ,在 Rt △ H M A 中根据正弦定义得出HM的长,在 Rt △ A M R 中, M R = A D = A B = 4 ,进而求出QR,QP,PR的长,从而得出P点的坐标。
三、计算题
17.【答案】解:(π﹣2016)0﹣2tan45°+( )﹣2
=1﹣2×1+
=﹣
【考点】实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值
【解析】【分析】利用零指数的意义,负指数的意义,特殊锐角三角函数值分别化简,再按照实数运算法则进行运算即可。
18.【答案】解:原式=[( ﹣ )]?
=
=
∵x=tan45°+2cos60°=1+2× =2,
∴原式= =
【考点】利用分式运算化简求值,特殊角的三角函数值
【解析】【分析】先将分式和x化简,然后将x的值代入即可求出答案.
19.【答案】解:原式=2-6× +1+2 ?
=2-2 +1+2
=3
【考点】实数的运算,特殊角的三角函数值
【解析】【分析】根据负指数的意义,0指数的意义,二次根式的性质,特殊锐角三角函数值,分别化简,再按实数的运算方法算出答案。
20.【答案】(1)解:原式=3 ﹣3× ﹣4﹣4(7﹣4 )=3 ﹣ ﹣4﹣28+16 =18 ﹣32
(2)解:原式=6× ﹣ × ﹣ =
【考点】实数的运算,负整数指数幂的运算性质,特殊角的三角函数值
【解析】【分析】(1)原式利用二次根式性质,特殊角的三角函数值,负整数指数幂法则,以及完全平方公式计算即可得到结果;(2)原式利用特殊角的三角函数值计算即可得到结果.
四、解答题
21.【答案】解:∵AB=100米,α=37°,
∴BC=AB?sinα=100sin37°,
∵AD=CE=1.5米,
∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米),
答:风筝离地面的高度BE为:61.5米
【考点】锐角三角函数的定义
【解析】【分析】根据正弦函数的定义,由BC=AB?sinα得出BC的长,根据矩形的性质得出AD=CE,根据线段的和差即可得出答案。
22.【答案】解:过O点作OD⊥AB交AB于D点. 在Rt△ADO中,
∵∠A=15°,AO=30,
∴OD=AO?sin15°=30×0.259=7.77(cm)
AD=AO?cos15°=30×0.966=28.98(cm)
又∵在Rt△BDO中,∠OBC=45°,
∴BD=OD=7.77(cm),
∴AB=AD+BD=36.75≈37(cm).
答:AB的长度为37cm
【考点】解直角三角形的应用
【解析】【分析】过O点作OD⊥AB交AB于D点,根据∠A=15°,AO=30可知OD=AO?sin15°,AD=AO?cos15°,在Rt△BDO中根据∠OBC=45°可知BD=OD,再根据AB=AD+BD即可得出结论.
23.【答案】解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000 米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000 米,
∴AB=BD﹣AD=2000 米.
答:此时渔政船和渔船相距2000 米.
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
24.【答案】解:过点C作CD⊥AB于点D,
设CD=x,
∵∠CBD=45°,
∴BD=CD=x,
在Rt△ACD中,∵tan ,
∴AD= = = = x,
由AD+BD=AB可得 x+x=10,
解得:x=5 ﹣5,
答:飞机飞行的高度为(5 ﹣5)km
【考点】解直角三角形的应用-仰角俯角问题
【解析】【分析】C作CD⊥AB,由∠CBD=45°知BD=CD=x,由∠ACD=30°知AD= = x,根据AD+BD=AB列方程求解可得.
五、综合题
25.【答案】(1)解:由题意得,sin∠BAH= = ,又AB=10米,
∴BH= AB=5米
(2)解:∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=5,AH=5 ,
∴BG=AH+AE=5 +15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5 +15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE= AE=15 .
∴CD=CG+GE﹣DE=5 +15+5﹣15 =20﹣10 .
答:广告牌CD的高度为(20﹣10 )米.
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)根据正弦的概念求出BH的长;(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE﹣DE即可求出广告牌的高度.
26.【答案】(1)证明:如图,
∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线
(2)证明:连接AC,如图2所示:
∵OF⊥BC,
∴ ,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴ ,
∴CE2=EH?EA
(3)解:连接BE,如图3所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为 ,sin∠BAE= ,
∴AB=5,BE=AB?sin∠BAE=5× =3,
∴EA= =4,
∵ ,
∴BE=CE=3,
∵CE2=EH?EA,
∴EH= ,
∴在Rt△BEH中,BH= .
【考点】圆周角定理,切线的判定,相似三角形的判定与性质,解直角三角形
【解析】【分析】(1)要证BD是⊙O的切线,只需证∠OBD=90°,因为∠OBC+∠BOD=90°,所以只须证∠ODB=∠OBC即可。由圆周角定理和已知条件易得∠ODB=∠ABC,则∠OBC+∠BOD=90°=∠ODB+∠BOD,由三角形内角和定理即可得∠OBD=90°;
(2)连接AC,要证CE2=EH?EA;只需证△CEH∽△AEC,已有公共角∠AEC,再根据圆周角定理可得∠CAE=∠ECB,即可证△CEH∽△AEC,可得比例式求解;
(3)连接BE,解直角三角形AEB和直角三角形BEH即可求解。
1 / 1
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
第23章解直角三角形专题训练(含精讲解析)
一、单选题(共10题;共30分)
1.如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( ??)
A.?1.25???????????????????????B.?0.8???????????????????????????C.?0.6???????????????????????????D.?0.625
2.cos45°的值是(?????)
A.???????????????????????????????B.?????????????????????????C.?????????????????????????????????????????D.?1
3.在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 , 则∠A的正切值( )
A.?缩小为原来的????????????????B.?扩大为原来的4倍????????????????
C.?缩小为原来的????????????????D.?没有变化
4.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A.?25+75??????????B.?50+50???????????C.?75+75???????????????D.?50+100
5.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠ABP=( )
A.? ??????B.?2 ?C.? ?D.?
6.(2015?威海)如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.?5÷tan26°=? ? ? ????B.?5÷sin26°=????????C.?5×cos26°=? ? ? ???????D.?5×tan26°
7.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A、A′的余弦值的关系为( )
A.?cosA=cosA′ B.?cosA=3cosA′ C.?3cosA=cosA′ D.?不能确定
8.如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为(?? )
A.???????????????????B.???????????????????????C.????????????????????????????????D.?
9.如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别在边AD、AB、BC、CD上,则tan∠DEH=( ????)
A.?????????????????????????????B.?????????????????????????????C.??????????????????????????????????????????D.?
10.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
A.?(4.8,6.4)???????????B.?(4,6)??????????????C.?(5.4,5.8)????????????????D.?(5,6)
二、填空题(共6题;共24分)
11.若sinA= ,则cos(90°﹣A)=________.
12.﹣13+ ﹣12sin30°=________.
13.计算:cos245°=________.
14.如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC=________.
15.如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ?.下列结论:
①△ADE∽△ACD;????? ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8;? ④0
其中正确的结论是________.(把你认为正确结论的序号都填上)
16.勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为________.
三、计算题(共4题;共31分)
17.计算:(π﹣2016)0﹣2tan45°+( )﹣2 .
18.先化简,再求值:( ﹣ )÷ ,其中x=tan45°+2cos60°.
19.计算:
20.计算:
(1) ﹣3tan30°﹣( )﹣2﹣4( ﹣2)2
(2)6tan230°﹣ sin60°﹣cos45°.
四、解答题(共4题;共36分)
21.如图,小明在操场上放风筝,已知风筝线AB长100? 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
22.如图,图①是某电脑液晶显示器的侧面图,显示屏AO可以绕点O旋转一定的角度.研究表明:显示屏顶端A与底座B的连线AB与水平线BC垂直时(如图②),人观看屏幕最舒适.此时测得∠BAO=15°,AO=30cm,∠OBC=45°,求AB的长度.(结果精确到1cm)(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, ≈1.414)
23.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
24.(2017?宿迁)如图所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
五、综合题(共2题;共29分)
25.如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH= ,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
26.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH?EA;
(3)若⊙O的半径为 ,sinA= ,求BH的长.
答案解析部分
一、单选题
1.【答案】B
【考点】等腰三角形的性质,锐角三角函数的定义
【解析】【解答】解:作AD⊥BC于D,如图,
∵AB=AC=5,
∴BD=CD= BC= ×8=4,
在Rt△ABD中,cosB= = .
故答案为:B.
【分析】作AD⊥BC于D根据等腰三角形的三线合一得出BD=CD,在Rt△ABD中根据余弦函数的定义得出cosB的值。
2.【答案】C
【考点】特殊角的三角函数值
【解析】
【分析】根据特殊角的三角函数值直接解答即可.
【解答】cos45°=.
故选C.
【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要熟练掌握.
3.【答案】D
【考点】锐角三角函数的定义
【解析】【解答】解:∵在Rt△ABC中,如果每个边都缩小为原来的 ,
∴锐角A的对边与邻边的比值不变,
∴锐角A的正切值不变.
故选D.
【分析】根据题意得到锐角A的对边与邻边的比值不变,然后根据正切的定义可判断锐角A的正切值不变.
4.【答案】D
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【解答】解:设AE=xm,在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面50m,
∴OE=50m,
∴OP′=OP=PE+OE=x+50,
∵∠P′AE=60°,
∴P′E=tan60°?AE=x,
∴OP′=P′E﹣OE=x﹣50,
∴x+50=x﹣50,
解得:x=50(+1)(m),
∴PO=PE+OE=50(+1+50=50+100(m),
即飞艇离开湖面的高度是(50+100)m;
故选:D.
【分析】设AE=x,则PE=AE=x,根据山顶A处高出水面50m,得出OE=50,OP′=x+50,根据∠P′AE=60°,得出P′E=x,从而列出方程,求出x的值即可.
5.【答案】A
【考点】锐角三角函数的定义,解直角三角形的应用﹣方向角问题
【解析】【分析】根据题意作出图形后知道北偏东30°与北偏西60°成直角,利用正切的定义求值即可.
【解答】∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°? BP=60×=40
∴tan∠ABP===
故选A.
【点评】本题考查了解直角三角形的应用,解题的关键是根据实际问题整理出直角三角形并利用正切的定义求值.
6.【答案】D
【考点】计算器—三角函数
【解析】【解答】解:由tanB=,得
AC=BC?tanB=5×tan26.
故选:D.
【分析】根据正切函数的定义,可得tanB=?,根据计算器的应用,可得答案.
7.【答案】A
【考点】锐角三角函数的增减性
【解析】【解答】解:根据锐角三角函数的概念,知
把Rt△ABC各边的长度都扩大3倍,那么它们的余弦值不变.
故选A.
【分析】锐角三角函数即为直角三角形中有关边的比值.
8.【答案】B
【考点】坐标与图形性质,圆周角定理,解直角三角形
【解析】【解答】解:连接EC,
∵∠COE=90°,
∴EC是⊙A的直径,
∵C(0,6),E(﹣8,0),O(0,0),
∴OC=6,OE=8,
由勾股定理得:EC=10,
∵∠OBC=∠OEC,
∴cos∠OBC=cos∠OEC= = = .
故答案为:B.
【分析】∠OBC不处在直角三角形中,因此需连直径转化∠OBC为∠OEC,且又处于直角三角形中,再利用余弦定义可求出.
9.【答案】A
【考点】勾股定理,相似三角形的性质,相似三角形的判定,锐角三角函数的定义
【解析】【解答】∵正方形ABCD的边长为10a,
∴∠A=∠B=90° ,AB=10a,
过点G作GP⊥ AD,垂足为P,则∠DPG=∠APG.
∴四边形APGB是矩形,
∴∠PGF+∠BGF=90°,PG=AB=10a,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠EGP+∠PGF=90°,
∴∠EGP=∠BGF
∴△BGF∽△PGE,
∴,
∴GB=AP=2a,
同理DE=2a,
∴PE=AD-AP-DE=6a,
∴EG==2a,
∴小正方形的边长为a,
∴DH==a
∴tan∠DEH==
故本题正确选项为A。
【分析】过点G作GP⊥ AD,垂足为P,可以得到△BGF∽△PGE,再根据相似三角形对应边成比例的性质列式求解即可得到DE和BG的长,根据勾股定理可求出EG的长,从而求出DH的长,再根据三角函数的定义得出答案。
10.【答案】A
【考点】翻折变换(折叠问题),解直角三角形
【解析】
【分析】设出A1点的坐标,先根据翻折变换的性质得出△A1BD的面积,作A1E⊥x轴于E,交DE于F,根据BC∥x轴可知A1E⊥BC,再由(1)中BD的值及三角形的面积公式可求出A1F的长,B点坐标,用待定是法求出过O、D两点的一次函数的解析式,把A1点的坐代入函数解析式即可.
【解答】∵BC∥AO,
∴∠BOA=∠OBC,
根据翻折不变性得,
∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2 ,
解得x=5.
∴BD=5,
∴S△BDO=×5×4=10;
设A1(a,4+b),作A1E⊥x轴于E,交DE于F,如下图所示:
∵BC∥x轴,
∴A1E⊥BC,
∵S△OAB=OA?AB=×8×4=16,S△BDO=10.
∴S△A1BD=BD?A1F=×5A1F=6,
解得A1F=,
∴A点的纵坐标为?,
∵BD=5,B(8,4)
∴D点坐标为(3,4),
∴过OC两点直线解析式为y=x,
把A点的坐标(a,)代入得,=a,
解得a=,
∴A点的坐标为(?,).即(4.8,6.4)
故选A.
二、填空题
11.【答案】
【考点】互余两角三角函数的关系
【解析】【解答】解:∵∠A与∠90°﹣A互余,
∴cos(90°﹣A)=sinA= .
故答案为 .
【分析】根据一个角的正弦值等于它的余角的余弦值即可求解.
12.【答案】-5
【考点】特殊角的三角函数值
【解析】【解答】解:原式=﹣1+2﹣12× =﹣1+2﹣6=﹣5,
故答案为:﹣5.
【分析】先依据有理数的乘方法则、算术平方根的性质、特殊锐角三角函数值进行化简,最后,在进行计算即可.
13.【答案】
【考点】特殊角的三角函数值
【解析】【解答】解:原式=()2== .
【分析】运用特殊角三角函数值计算.
14.【答案】
【考点】切线的性质,解直角三角形
【解析】【解答】解:连接OD,则OD⊥BD,
过E作EH⊥BC,垂足为H,如图,
∴EH∥OD,
∵EF∥BC,OE=OD,
∴四边形EODH是正方形,
∴EH=HD=OD=5,
又∵BD=12,
∴BH=7,
在Rt△BEH中,tan∠ABC= = .
【分析】由EF∥BC,OE=OD,得到四边形EODH是正方形,根据正方形的性质,得到四边相等,求出在Rt△BEH中,tan∠ABC.
15.【答案】①②④
【考点】二次函数的最值,全等三角形的判定与性质,相似三角形的判定与性质,解直角三角形的应用
【解析】【解答】作AH⊥BC于H , 如图,
∵AB=AC ,
∴∠B=∠C=α , BH=CH ,
而∠ADE=∠B=α ,
∴∠ADE=∠C ,
而∠DAE=∠CAD ,
∴△ADE∽△ACD , 所以①正确;
在Rt△ABH中,cosB= ,
∴BH=10× ?=8,
∴BC=2BH=16,
当BD=6,则CD=10,
∵∠ADC=∠B+∠BAD ,
而∠ADE=∠B=α ,
∴∠EDC=∠BAD ,
在△ABD与△DCE中
,
∴△ABD≌△DCE , 所以②正确;
∵∠B=∠C , ∠BAD=∠CDE ,
∴△ABD∽△DCE ,
△DCE为直角三角形,当∠DEC=90°,则∠ADB=90°,BD为8;
当∠EDC=90°,则∠BAD=90°,BD= ,所以③错误;
设BD=x , 则CD=16-x ,
由△ABD∽△DCE得 ?,即 ,
∴CE=- ?,
∴CE的最大值为6.4,
∴0<CE≤6.4,所以④正确.
故答案为:①②④.
【分析】①利用三个角相等的两个三角形相似来证明;②利用角相等,将所给的余弦函数变为∠B的余弦函数,从而利用角边角证得△ABD≌△DCE;③利用三角形相似对应边成比例,再结合所求及所给线段的长度求得BD的长度;④由三角形相似对应边成比例用BD的表示出CE的长度,再利用二次函数的图像特征计算出CE的取值范围.
16.【答案】(7 +6,0)
【考点】全等三角形的判定与性质,等边三角形的判定与性质,锐角三角函数的定义
【解析】【解答】延长BA交QR于点M , 连接AR , AP ,
在△ABC与△GFC中,
?
?
?
????
又∵ ?
?
?
?
?
∴△QHG是等边三角形.
?
则 ?
在 中, ??
在 中, ?
? ?
?
?
∴点P的坐标为
故答案为:
【分析】 延长BA交QR于点M , 连接AR , AP , 先利用SAS判断出△ABC≌△GFC,然后根据全等三角形的性质得出∠ C G F = ∠ B A C = 30 ? , 进一步得出HGQ=60? , 然后周角的定义得出BAC+∠DAH=180,再根据二直线平行同旁内角互补得出RHA+∠DAH=180? , 再根据同角的补角相等得出RHA=∠BAC=30? , 进而判断出△QHG是等边三角形.根据余弦的定义得出AC的长,从而根据正方形的性质得出 Q H = H A = H G = A C = 2? ,在 Rt △ H M A 中根据正弦定义得出HM的长,在 Rt △ A M R 中, M R = A D = A B = 4 ,进而求出QR,QP,PR的长,从而得出P点的坐标。
三、计算题
17.【答案】解:(π﹣2016)0﹣2tan45°+( )﹣2
=1﹣2×1+
=﹣
【考点】实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值
【解析】【分析】利用零指数的意义,负指数的意义,特殊锐角三角函数值分别化简,再按照实数运算法则进行运算即可。
18.【答案】解:原式=[( ﹣ )]?
=
=
∵x=tan45°+2cos60°=1+2× =2,
∴原式= =
【考点】利用分式运算化简求值,特殊角的三角函数值
【解析】【分析】先将分式和x化简,然后将x的值代入即可求出答案.
19.【答案】解:原式=2-6× +1+2 ?
=2-2 +1+2
=3
【考点】实数的运算,特殊角的三角函数值
【解析】【分析】根据负指数的意义,0指数的意义,二次根式的性质,特殊锐角三角函数值,分别化简,再按实数的运算方法算出答案。
20.【答案】(1)解:原式=3 ﹣3× ﹣4﹣4(7﹣4 )=3 ﹣ ﹣4﹣28+16 =18 ﹣32
(2)解:原式=6× ﹣ × ﹣ =
【考点】实数的运算,负整数指数幂的运算性质,特殊角的三角函数值
【解析】【分析】(1)原式利用二次根式性质,特殊角的三角函数值,负整数指数幂法则,以及完全平方公式计算即可得到结果;(2)原式利用特殊角的三角函数值计算即可得到结果.
四、解答题
21.【答案】解:∵AB=100米,α=37°,
∴BC=AB?sinα=100sin37°,
∵AD=CE=1.5米,
∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米),
答:风筝离地面的高度BE为:61.5米
【考点】锐角三角函数的定义
【解析】【分析】根据正弦函数的定义,由BC=AB?sinα得出BC的长,根据矩形的性质得出AD=CE,根据线段的和差即可得出答案。
22.【答案】解:过O点作OD⊥AB交AB于D点. 在Rt△ADO中,
∵∠A=15°,AO=30,
∴OD=AO?sin15°=30×0.259=7.77(cm)
AD=AO?cos15°=30×0.966=28.98(cm)
又∵在Rt△BDO中,∠OBC=45°,
∴BD=OD=7.77(cm),
∴AB=AD+BD=36.75≈37(cm).
答:AB的长度为37cm
【考点】解直角三角形的应用
【解析】【分析】过O点作OD⊥AB交AB于D点,根据∠A=15°,AO=30可知OD=AO?sin15°,AD=AO?cos15°,在Rt△BDO中根据∠OBC=45°可知BD=OD,再根据AB=AD+BD即可得出结论.
23.【答案】解:在Rt△CDA中,∠ACD=30°,CD=3000米,
∴AD=CDtan∠ACD=1000 米,
在Rt△CDB中,∠BCD=60°,
∴BD=CDtan∠BCD=3000 米,
∴AB=BD﹣AD=2000 米.
答:此时渔政船和渔船相距2000 米.
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】在Rt△CDB中求出BD,在Rt△CDA中求出AD,继而可得AB,也即此时渔政船和渔船的距离.
24.【答案】解:过点C作CD⊥AB于点D,
设CD=x,
∵∠CBD=45°,
∴BD=CD=x,
在Rt△ACD中,∵tan ,
∴AD= = = = x,
由AD+BD=AB可得 x+x=10,
解得:x=5 ﹣5,
答:飞机飞行的高度为(5 ﹣5)km
【考点】解直角三角形的应用-仰角俯角问题
【解析】【分析】C作CD⊥AB,由∠CBD=45°知BD=CD=x,由∠ACD=30°知AD= = x,根据AD+BD=AB列方程求解可得.
五、综合题
25.【答案】(1)解:由题意得,sin∠BAH= = ,又AB=10米,
∴BH= AB=5米
(2)解:∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.
∵由(1)得:BH=5,AH=5 ,
∴BG=AH+AE=5 +15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5 +15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE= AE=15 .
∴CD=CG+GE﹣DE=5 +15+5﹣15 =20﹣10 .
答:广告牌CD的高度为(20﹣10 )米.
【考点】解直角三角形的应用﹣仰角俯角问题
【解析】【分析】(1)根据正弦的概念求出BH的长;(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE﹣DE即可求出广告牌的高度.
26.【答案】(1)证明:如图,
∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线
(2)证明:连接AC,如图2所示:
∵OF⊥BC,
∴ ,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴ ,
∴CE2=EH?EA
(3)解:连接BE,如图3所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为 ,sin∠BAE= ,
∴AB=5,BE=AB?sin∠BAE=5× =3,
∴EA= =4,
∵ ,
∴BE=CE=3,
∵CE2=EH?EA,
∴EH= ,
∴在Rt△BEH中,BH= .
【考点】圆周角定理,切线的判定,相似三角形的判定与性质,解直角三角形
【解析】【分析】(1)要证BD是⊙O的切线,只需证∠OBD=90°,因为∠OBC+∠BOD=90°,所以只须证∠ODB=∠OBC即可。由圆周角定理和已知条件易得∠ODB=∠ABC,则∠OBC+∠BOD=90°=∠ODB+∠BOD,由三角形内角和定理即可得∠OBD=90°;
(2)连接AC,要证CE2=EH?EA;只需证△CEH∽△AEC,已有公共角∠AEC,再根据圆周角定理可得∠CAE=∠ECB,即可证△CEH∽△AEC,可得比例式求解;
(3)连接BE,解直角三角形AEB和直角三角形BEH即可求解。
1 / 1
