第三章 圆单元检测试卷（有答案）

中小学教育资源及组卷应用平台


2018-2019学年度广东省揭西县宝塔实验学校九年级数学下册
圆单元过关检测1（2018.12）
班级_____________ 姓名_____________ 座号_____________ 分数_____________
一．选择题（本大题10小题，每小题3分，共30分）
1．如图1,△ABD的三个顶点在☉O上,AB是直径,点C在☉O上,且∠ABD=52°,则∠BCD=(　　)
A.32° B.38° C.52° D.66°
2.如图2，AB是⊙O的直径，BC是⊙O的弦．若∠OBC＝60°，则∠BAC的度数是(　　)
A．75° B．60° C．45° D．30°
3．如图3,点A、B、C、D在☉O上,∠AOC=140°,点B是弧AC的中点,则∠D的度数是(　　)
A.70° B.55° C.35.5° D.35°
4.如图4，AB是⊙O的直径，CD为弦，CD⊥AB且相交于点E，则下列结论中不成立的是(　　)
A．∠A＝∠D B.＝ C．∠ACB＝90° D．∠COB＝3∠D





图1 图2 图3 图4
5．如图,扇形OMN所在圆的半径为3,弧MN的长为6,则扇形的面积是(　　)
A.9 B.8 C.7 D.6
6.一个扇形的弧长是10π cm,面积是60π cm2,则此扇形的圆心角的度数是(　　)
A.300° B.150° C.120° D.75°
7．如图,在☉O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为(　　)
A.40° B.50° C.80° D.100°
8.如图，四边形ABCD是菱形，∠A＝60°，AB＝2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是(　　)
A.－ B.－ C．π－ D．π－
9. 如图,AB是☉O的直径,点P是☉O外一点,PO交☉O于点C,连接BC,PA.若∠P=40°,当PA与☉O相切时,∠B=(　　)
A.20° B.25° C.30° D.40°
10． 如图,在平面直角坐标系中,☉M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是(　　)
A.10 B. C. D.

二、填空题（每小题4分，共24分）
11.如图5，OA，OB是⊙O的半径，点C在⊙O上，连接AC，BC.若∠AOB＝120°，则∠ACB＝________°.

12.如图6，P、Q分别是⊙O的内接正五边形的边AB，BC上的点，BP＝CQ，则∠POQ＝________．
13.如图7，四边形ABCD内接于⊙O，BD是⊙O的直径，AC与BD相交于点E，AC=BC，DE=3，AD=5，则⊙O的半径为________．
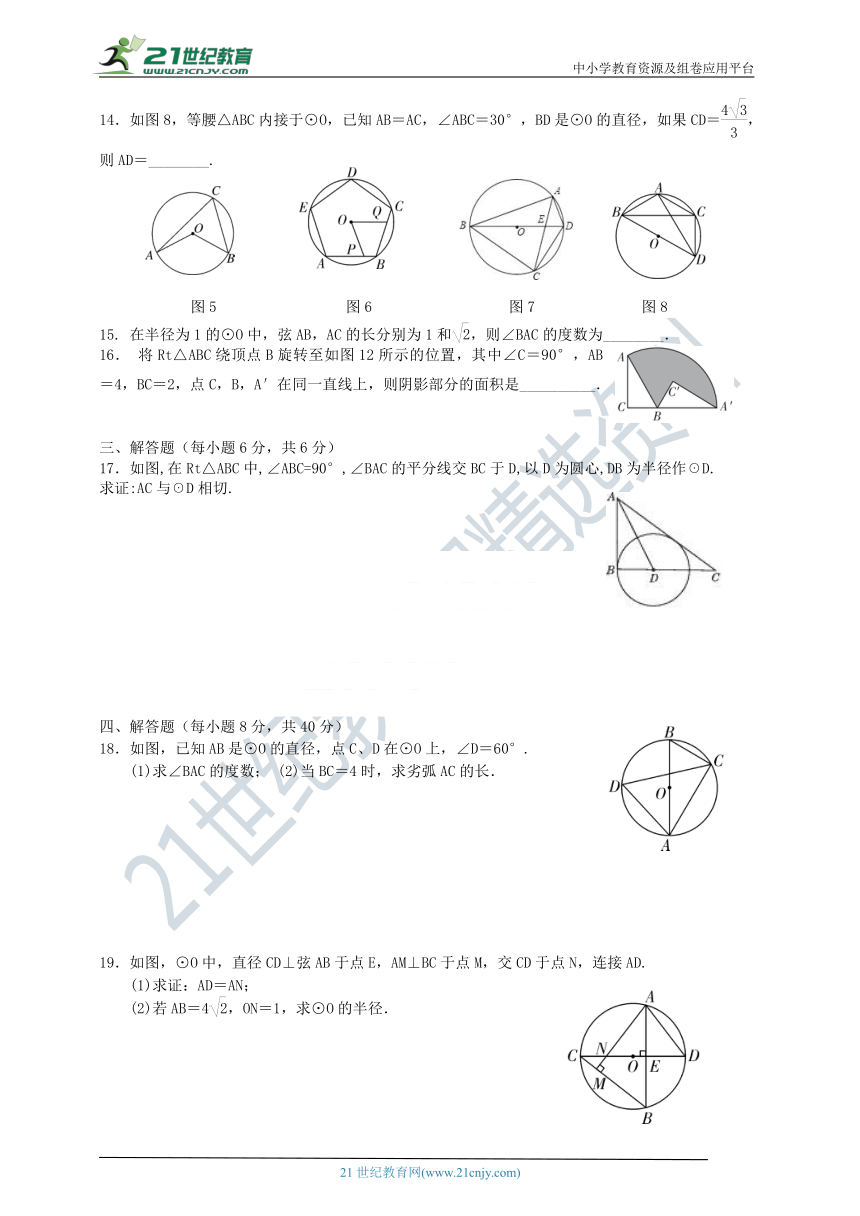
14．如图8，等腰△ABC内接于⊙O，已知AB＝AC，∠ABC＝30°，BD是⊙O的直径，如果CD＝，则AD＝________.




图5 图6 图7 图8
15. 在半径为1的⊙O中，弦AB，AC的长分别为1和，则∠BAC的度数为________．
16． 将Rt△ABC绕顶点B旋转至如图12所示的位置，其中∠C＝90°，AB＝4，BC＝2，点C，B，A′在同一直线上，则阴影部分的面积是__________．

三、解答题（每小题6分，共6分）
17．如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB为半径作☉D.
求证:AC与☉D相切.








四、解答题（每小题8分，共40分）
18．如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D＝60°.
(1)求∠BAC的度数； (2)当BC＝4时，求劣弧AC的长．










19．如图，⊙O中，直径CD⊥弦AB于点E，AM⊥BC于点M，交CD于点N，连接AD.
(1)求证：AD＝AN；
(2)若AB＝4，ON＝1，求⊙O的半径．

















20.如图，AB是半圆O的直径，PA，PC分别与半圆相切于点A，D，BC⊥PC于点C，连接PO，AD，BD.
求证：(1)PO⊥AD；(2)BD平分∠ABC.





















21.已知：如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．(1)求证：DE与⊙O相切；(2)若∠B＝30°，AB＝8，求DE的长．















22．如图，⊙O是△ABC的外接圆，AC为直径，过C点作⊙O的切线，与AB延长线交于点D，E为CD的中点，连接BE，OE，且BC与OE相交于点F.
(1)求证：BE与⊙O相切；
(2)求证：CD2＝2BD·OE；
(3)若cos D＝，BE＝4，求AB的长．















选择题
B 2. D　3. D 4. D 5. A 6. D 7. C　8. B　9. B　10. 　
二．填空题
11.60　12. 72°　13. 7.5 14. 4　15. 15°或105°　16.π－2
三.解答题
17.证明:如图,过点D作DE⊥AC,垂足为E.
∵AD平分∠BAC,BD⊥AB,DE⊥AC,
∴DE=DB,即点D到AC的距离等于☉D的半径.∴AC与☉D相切
四．解答题
18.解：(1)∵∠ABC与∠D都是弧AC所对的圆周角，
∴∠ABC＝∠D＝60°，
∵AB是O的直径，
∴∠ACB＝90°，
∴∠BAC＝180°－90°－60°＝30°；
(2)如解图，连接OC，
∵OB＝OC，∠ABC＝60°，
∴△OBC是等边三角形
∴OC＝BC＝4，∠BOC＝60°，
∴∠AOC＝120°，
∴劣弧AC的长为＝π.

19.(1)证明：∵∠BAD与∠BCD是同弧所对的圆周角，
∴∠BAD＝∠BCD，∵AE⊥CD，AM⊥BC，
∴∠AEN＝∠AMC＝90°，∵∠ANE＝∠CNM，
∴∠BAM＝∠BCD，∴∠BAM＝∠BAD，
在△ANE与△ADE中，
，
∴△ANE≌△ADE(ASA)，
∴AN＝AD；
(2)解：∵AB＝4，AE⊥CD,
∴AE＝AB＝2，
又∵ON＝1，
∴设NE＝x，则OE＝x－1，NE＝ED＝x，OD＝OE＋ED＝2x－1，
如解图，连接AO，则AO＝OD＝2x－1，
∵△AOE是直角三角形，AE＝2，OE＝x－1，AO＝2x－1，
∴(2)2＋(x－1)2＝(2x－1)2，
解得x1＝2，x2＝－(舍)，
∴AO＝2x－1＝3，即⊙O的半径为3.

20．证明：(1)如解图，连接OD.
∵PA、PC分别与半圆相切于点A、D，O为圆心，∴OA⊥PA，OD⊥PD.
在Rt△PAO和Rt△PDO中，
eq \b\lc\{(\a\vs4\al\co1(AO＝DO,PO＝PO))，
∴Rt△PAO≌Rt△PDO(HL)，
∴PA＝PD，∠APO＝∠DPO.
设PO与AD交于点H，则在△PAH和△PDH中，
，
∴△PAH≌△PDH(SAS)，
∴∠PHA＝∠PHD＝90°，
即PO⊥AD；
(2)由(1)知OD⊥PC，又由题意知BC⊥PC，∴OD∥BC，
∴∠ODB＝∠DBC.又∵OD＝OB，∴∠ODB＝∠OBD，∴∠OBD＝∠DBC，
∴BD平分∠ABC.
21.(1)证明：如图，连接OD，则OD＝OB，∴∠B＝∠ODB.
∵AB＝AC，∴∠B＝∠C.
∴∠ODB＝∠C.∴OD∥AC.∴∠ODE＝∠DEC＝90°.
∴DE是⊙O的切线．
(2)解：如图，连接AD，∵AB是⊙O的直径，
∴∠ADB＝90°.
∴BD＝AB·cosB＝8×＝4 .
又AB＝AC，∴CD＝BD＝4 ，∠C＝∠B＝30°.∴DE＝CD＝2 .

22.(1)证明：如图3，连接OB，
∵AC为⊙O的直径，∴∠ABC＝90°.
∴∠DBC＝90°.
∵在Rt△DBC中，E是CD的中点，
∴BE＝CE＝DE＝CD.
∴∠ECF＝∠EBF.
∵OC＝OB，∴∠OCF＝∠OBF.
∴∠OBE＝∠EBF＋∠OBF＝∠ECF＋∠OCF＝90°.
∴BE与⊙O相切．
(2)证明：在Rt△ACD中，∠A＋∠D＝90°，
在Rt△CBD中，∠BCD＋∠D＝90°，∴∠A＝∠BCD.
又∠D＝∠D，∴△CBD∽△ACD.
∴＝.
∴CD2＝BD·AD.
∵O是AC的中点，E是CD的中点，∴AD＝2OE.
∴CD2＝2BD·OE.
(3)解：由(2)知，BE＝CD，又BE＝4，∴CD＝8.
在Rt△BCD中，＝cos D＝，∴BD＝.
在Rt△ACD中，＝cos D＝，∴AD＝12.
∴AB＝AD－BD＝.











21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)