湘教版九年级数学下册《第二章圆》单元检测试卷(有答案)
文档属性
| 名称 | 湘教版九年级数学下册《第二章圆》单元检测试卷(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 147.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-09 00:00:00 | ||
图片预览



文档简介
湘教版九年级数学下册 第二章 圆 单元检测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. ⊙??中,直径????=??,弦????=??,则??与??大小为( )
A.??>??
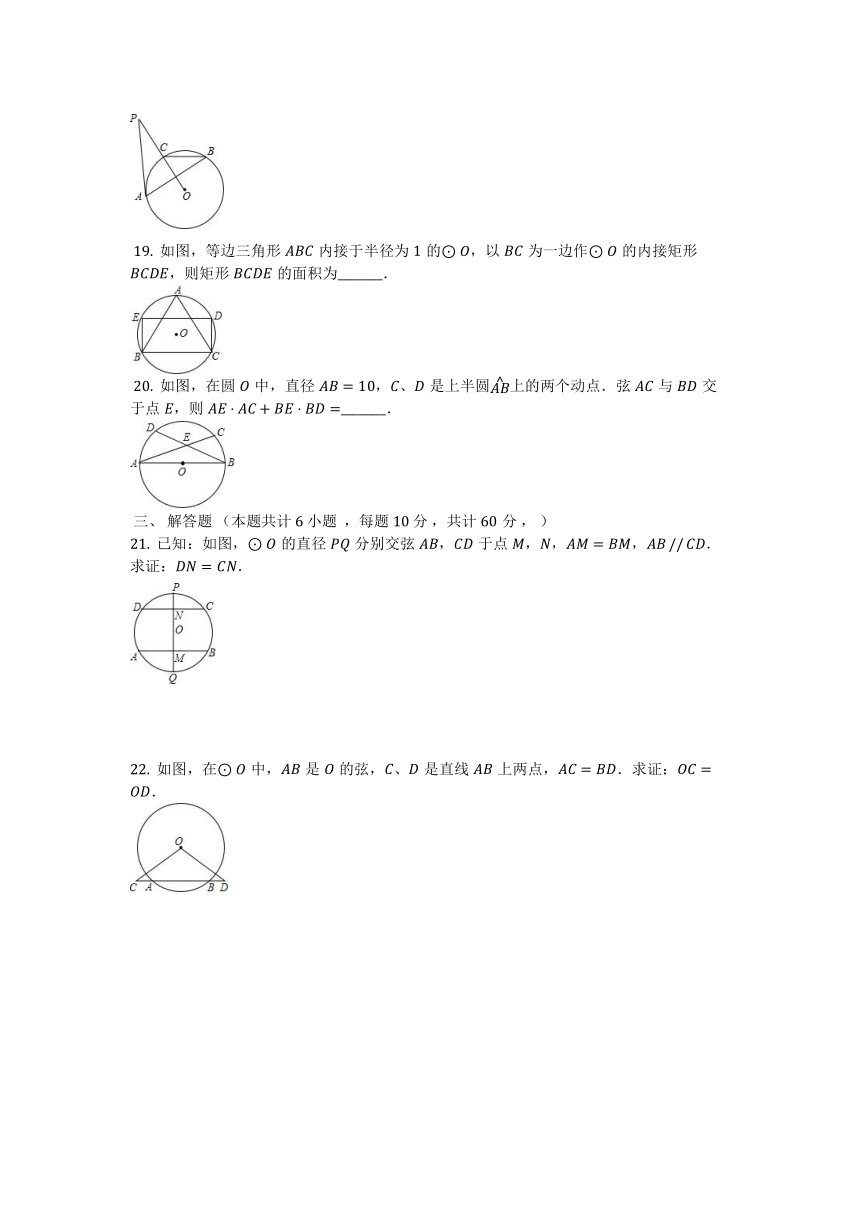
B.??≥??
C.??D.??≤??
?2. 如图,????、????是⊙??的两条切线,??、??是切点,若∠??=
70
°
,则∠??????的度数为( )
/
A.
130
°
B.
120
°
C.
110
°
D.
100
°
?3. 如图,四边形????????内接于⊙??,若它的一个外角∠??????=
72
°
,则∠??????等于( )
/
A.
144
°
B.
70
°
C.
110
°
D.
140
°
?4. 下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.到圆心的距离大于半径的直线 D.到圆心的距离小于半径的直线
?5. 如图,点??,??,??在⊙??上,∠??=
50
°
,则∠??????的度数为( )
/
A.
40
°
B.
50
°
C.
80
°
D.
100
°
?6. 如图,⊙??△??????的三条边所得的弦长相等,则下列说法正确的是( )
/
A.点??是△??????的内心
B.点??是△??????的外心
C.△??????是正三角形
D.△??????是等腰三角形
?7. 一条弦把圆周分成1:4两部分,则这条弦所对的圆周角为( )
A.
36
°
B.
144
°
C.
150
°
D.
36
°
或
144
°
?8. 如图,割线??????交⊙??于??、??两点,且????:????=2:1,????交⊙??于??,????=3,????=2,则????的长为( )
/
A.2
3
B.
14
C.2
6
D.
10
?9. 如图,????、????、????分别切⊙??于??、??、??,????交????、????于??、??两点,若∠??=
40
°
,则∠??????+∠??????的度数为( )
/
A.
50
°
B.
62
°
C.
66
°
D.
70
°
?10. 如图,在等边△??????中,点??在边????上,⊙??过点??且分别与边????、????相交于点??、??、??是????上的点,判断下列说法错误的是( )
/
A.若????⊥????,则????是⊙??的切线 B.若????是⊙??的切线,则????⊥????
C.若????=????,则????是⊙??的切线 D.若????=
3
2
????,则????是⊙??的切线
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 同一个圆的中内接正三角形与其外切正三角形的周长比是________,面积比是________.
?12. 如图,点??,??,??,??在⊙??上,∠??????=
40
°
,∠??????=
112
°
,??是????中点,则∠??????的度数为________.
/
?13. 在半径为1的圆中,长度等于
2
的弦所对的圆心角是________度.
?14. 半径为18的圆中,
120
°
的圆心角所对的弧长是________.
?15. ⊙??的半径为10????,??、??、??三点到圆心??的距离分别为8????、10????、12????,则点??、??、??与⊙??的位置关系是:点??在________;点??在________;点??在________.
?16. 如图,点??为△??????的内心,点??为△??????的外心,∠??=
140
°
,则∠??为________.
/
?17. 四边形????????是⊙??的内接四边形,且∠??=∠??,则∠??=________度.
/
?18. 如图,????与⊙??相切,切点为??,????交⊙??于点??,点??是优弧??????上一点,若∠??????=
32
°
,则∠??的度数为________.
/
?19. 如图,等边三角形??????内接于半径为1的⊙??,以????为一边作⊙??的内接矩形????????,则矩形????????的面积为________.
/
?20. 如图,在圆??中,直径????=10,??、??是上半圆
????
上的两个动点.弦????与????交于点??,则?????????+?????????=________.
/
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , )
21. 已知:如图,⊙??的直径????分别交弦????,????于点??,??,????=????,?????//?????. 求证:????=????.
/
?
22. 如图,在⊙??中,????是??的弦,??、??是直线????上两点,????=????.求证:????=????.
/
?
23. 如图,梯形????????中,?????//?????,∠??=
90
°
.以????为直径作⊙??交????于点??,????的中点??恰好在⊙??上.
/
(1)????是⊙??的切线吗?请说明理由;
(2)若????=2,????=6,求
????
的长度(结果保留??).
?
24. 如图,△??????内接于⊙??,且????为⊙??的直径,∠??????的平分线交⊙??于点??,过点??作⊙??的切线????交????的延长线于点??,过点??作????⊥????于点??,过点??作????⊥????于点??.试猜想线段????、????、????之间的关系,并加以证明.
/
?
25. 如图所示,已知????是⊙??的直径,直线??与⊙??相切于点??,
????
=
????
,????交????于??,????⊥直线??,垂足
/
为??,????交⊙??于??.
(1)图中哪条线段与????相等?试证明你的结论;
(2)若sin∠??????=
5
5
,????=4,求????的值.
?
26. 如图,在????△??????中,∠??????=
90
°
,以????为直径的⊙??与????边交于点??,过点??作⊙??的切线
/
,交????于点??.
(1)求证:点??是边????的中点;
(2)若????=3,????=2
6
,求⊙??的直径????的长度;
(3)若以点??,??,??,??为顶点的四边形是正方形,试判断△??????的形状,并说明理由.
答案
1. B
2. C
3. A
4. B
5. D
6. A
7. D
8. B
9. D
10. C
11. 1:21:4
12.
62
°
13. 90
14. 12??
15. 圆内圆上圆外
16.
125
°
17. 90
18.
26
°
19.
3
20. 100
21. 证明:∵????是直径,????=????, ∴????⊥????于??. 又∵?????//?????, ∴????⊥????于??. ∴????=????.
22. 证明:作????⊥????于??,如图, 则????=????, ∵????=????, ∴????+????=????+????, 即????=????, ∴????垂直平分????, ∴????=????.
/
23. 解:(1)????是⊙??的切线.理由如下: 连接????. ∵??是????中点,??是????中点, ∴????是直角梯形????????的中位线, ∴?????//??????//?????, ∴∠??????=∠??=
90
°
, 又∵????是⊙??的半径, ∴????是⊙??的切线;
/
(2)连接????、????. 由(1)得????=
????+????
2
=4, ∴????=????=4, ∵????是⊙??的直径, ∴∠??????=
90
°
, ∵直角梯形????????中,∠??=∠??=
90
°
, ∴四边形????????是矩形. ∴????=????=2, ∴????=?????????=4, ∴????=????=????=4, ∴∠??????=
60
°
, ∴
????
的长度=
60×4??
180
=
4
3
??.
24. 证明:????=????+????.理由如下: ∵????为⊙??的直径, ∴∠??????=
90
°
, ∵∠??????的平分线交⊙??于点??, ∴∠??????=∠??????=
45
°
, 又∵????⊥????, ∴△??????等腰直角三角形, ∴????=????, ∵∠??????的平分线交⊙??于点??, ∴∠??????=
45
°
, 又∵????⊥????, ∴△??????为等腰直角三角形, ∴????=????, ∴????=????=????+????=????+????.
25. 解:(1)????=????,理由如下: 连接????、????、????; ∵
????
=
????
, ∴????⊥????, ∴
????
=
????
,即∠??=∠??????; ∵直线??切⊙??于??, ∴∠??????=∠??=∠??????, ∴∠??????=∠??????, ∴
????
=
????
,????=????; ∴????=????; △??????和△??????中,????=????、????=????,∠??????=∠??????=
90
°
, ∴????△???????????△??????,则????=????.
/
(2)∵????切⊙??于??, ∴∠??????=∠??????,即sin∠??????=sin∠??????=
5
5
; 在????△??????中,????=????=4,????=????÷sin∠??????=4
5
; ∴????=????=4
5
; 在????△??????中,????⊥????,由射影定理得: ??
??
2
=?????????,即????=??
??
2
÷????=20.
26. (1)证明:连接????; ∵∠??????=
90
°
,????为直径, ∴????为⊙??的切线; 又∵????也为⊙??的切线, ∴????=????, 又∵∠??????=
90
°
, ∴∠??????+∠??????=
90
°
, ∴∠??????+∠??=
90
°
又∵∠??+∠??=
90
°
, ∴∠??????=∠??, ∴????=????, ∴????=????,即点??是边????的中点;
/
(2)解:∵????,????分别是⊙??的切线和割线, ∴??
??
2
=?????????, ∴(2????
)
2
=?????????,即?????2
6
=36, ∴????=3
6
, 在????△??????中,由勾股定理得 ????=
??
??
2
???
??
2
=
(3
6
)
2
?
6
2
=3
2
;(3)解:△??????是等腰直角三角形. 理由:∵四边形????????为正方形, ∴∠??????=∠??????=
90
°
,即?????//?????, 又∵点??是边????的中点, ∴????=2????=????, ∴△??????是等腰直角三角形.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. ⊙??中,直径????=??,弦????=??,则??与??大小为( )
A.??>??
B.??≥??
C.??D.??≤??
?2. 如图,????、????是⊙??的两条切线,??、??是切点,若∠??=
70
°
,则∠??????的度数为( )
/
A.
130
°
B.
120
°
C.
110
°
D.
100
°
?3. 如图,四边形????????内接于⊙??,若它的一个外角∠??????=
72
°
,则∠??????等于( )
/
A.
144
°
B.
70
°
C.
110
°
D.
140
°
?4. 下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.到圆心的距离大于半径的直线 D.到圆心的距离小于半径的直线
?5. 如图,点??,??,??在⊙??上,∠??=
50
°
,则∠??????的度数为( )
/
A.
40
°
B.
50
°
C.
80
°
D.
100
°
?6. 如图,⊙??△??????的三条边所得的弦长相等,则下列说法正确的是( )
/
A.点??是△??????的内心
B.点??是△??????的外心
C.△??????是正三角形
D.△??????是等腰三角形
?7. 一条弦把圆周分成1:4两部分,则这条弦所对的圆周角为( )
A.
36
°
B.
144
°
C.
150
°
D.
36
°
或
144
°
?8. 如图,割线??????交⊙??于??、??两点,且????:????=2:1,????交⊙??于??,????=3,????=2,则????的长为( )
/
A.2
3
B.
14
C.2
6
D.
10
?9. 如图,????、????、????分别切⊙??于??、??、??,????交????、????于??、??两点,若∠??=
40
°
,则∠??????+∠??????的度数为( )
/
A.
50
°
B.
62
°
C.
66
°
D.
70
°
?10. 如图,在等边△??????中,点??在边????上,⊙??过点??且分别与边????、????相交于点??、??、??是????上的点,判断下列说法错误的是( )
/
A.若????⊥????,则????是⊙??的切线 B.若????是⊙??的切线,则????⊥????
C.若????=????,则????是⊙??的切线 D.若????=
3
2
????,则????是⊙??的切线
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 同一个圆的中内接正三角形与其外切正三角形的周长比是________,面积比是________.
?12. 如图,点??,??,??,??在⊙??上,∠??????=
40
°
,∠??????=
112
°
,??是????中点,则∠??????的度数为________.
/
?13. 在半径为1的圆中,长度等于
2
的弦所对的圆心角是________度.
?14. 半径为18的圆中,
120
°
的圆心角所对的弧长是________.
?15. ⊙??的半径为10????,??、??、??三点到圆心??的距离分别为8????、10????、12????,则点??、??、??与⊙??的位置关系是:点??在________;点??在________;点??在________.
?16. 如图,点??为△??????的内心,点??为△??????的外心,∠??=
140
°
,则∠??为________.
/
?17. 四边形????????是⊙??的内接四边形,且∠??=∠??,则∠??=________度.
/
?18. 如图,????与⊙??相切,切点为??,????交⊙??于点??,点??是优弧??????上一点,若∠??????=
32
°
,则∠??的度数为________.
/
?19. 如图,等边三角形??????内接于半径为1的⊙??,以????为一边作⊙??的内接矩形????????,则矩形????????的面积为________.
/
?20. 如图,在圆??中,直径????=10,??、??是上半圆
????
上的两个动点.弦????与????交于点??,则?????????+?????????=________.
/
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , )
21. 已知:如图,⊙??的直径????分别交弦????,????于点??,??,????=????,?????//?????. 求证:????=????.
/
?
22. 如图,在⊙??中,????是??的弦,??、??是直线????上两点,????=????.求证:????=????.
/
?
23. 如图,梯形????????中,?????//?????,∠??=
90
°
.以????为直径作⊙??交????于点??,????的中点??恰好在⊙??上.
/
(1)????是⊙??的切线吗?请说明理由;
(2)若????=2,????=6,求
????
的长度(结果保留??).
?
24. 如图,△??????内接于⊙??,且????为⊙??的直径,∠??????的平分线交⊙??于点??,过点??作⊙??的切线????交????的延长线于点??,过点??作????⊥????于点??,过点??作????⊥????于点??.试猜想线段????、????、????之间的关系,并加以证明.
/
?
25. 如图所示,已知????是⊙??的直径,直线??与⊙??相切于点??,
????
=
????
,????交????于??,????⊥直线??,垂足
/
为??,????交⊙??于??.
(1)图中哪条线段与????相等?试证明你的结论;
(2)若sin∠??????=
5
5
,????=4,求????的值.
?
26. 如图,在????△??????中,∠??????=
90
°
,以????为直径的⊙??与????边交于点??,过点??作⊙??的切线
/
,交????于点??.
(1)求证:点??是边????的中点;
(2)若????=3,????=2
6
,求⊙??的直径????的长度;
(3)若以点??,??,??,??为顶点的四边形是正方形,试判断△??????的形状,并说明理由.
答案
1. B
2. C
3. A
4. B
5. D
6. A
7. D
8. B
9. D
10. C
11. 1:21:4
12.
62
°
13. 90
14. 12??
15. 圆内圆上圆外
16.
125
°
17. 90
18.
26
°
19.
3
20. 100
21. 证明:∵????是直径,????=????, ∴????⊥????于??. 又∵?????//?????, ∴????⊥????于??. ∴????=????.
22. 证明:作????⊥????于??,如图, 则????=????, ∵????=????, ∴????+????=????+????, 即????=????, ∴????垂直平分????, ∴????=????.
/
23. 解:(1)????是⊙??的切线.理由如下: 连接????. ∵??是????中点,??是????中点, ∴????是直角梯形????????的中位线, ∴?????//??????//?????, ∴∠??????=∠??=
90
°
, 又∵????是⊙??的半径, ∴????是⊙??的切线;
/
(2)连接????、????. 由(1)得????=
????+????
2
=4, ∴????=????=4, ∵????是⊙??的直径, ∴∠??????=
90
°
, ∵直角梯形????????中,∠??=∠??=
90
°
, ∴四边形????????是矩形. ∴????=????=2, ∴????=?????????=4, ∴????=????=????=4, ∴∠??????=
60
°
, ∴
????
的长度=
60×4??
180
=
4
3
??.
24. 证明:????=????+????.理由如下: ∵????为⊙??的直径, ∴∠??????=
90
°
, ∵∠??????的平分线交⊙??于点??, ∴∠??????=∠??????=
45
°
, 又∵????⊥????, ∴△??????等腰直角三角形, ∴????=????, ∵∠??????的平分线交⊙??于点??, ∴∠??????=
45
°
, 又∵????⊥????, ∴△??????为等腰直角三角形, ∴????=????, ∴????=????=????+????=????+????.
25. 解:(1)????=????,理由如下: 连接????、????、????; ∵
????
=
????
, ∴????⊥????, ∴
????
=
????
,即∠??=∠??????; ∵直线??切⊙??于??, ∴∠??????=∠??=∠??????, ∴∠??????=∠??????, ∴
????
=
????
,????=????; ∴????=????; △??????和△??????中,????=????、????=????,∠??????=∠??????=
90
°
, ∴????△???????????△??????,则????=????.
/
(2)∵????切⊙??于??, ∴∠??????=∠??????,即sin∠??????=sin∠??????=
5
5
; 在????△??????中,????=????=4,????=????÷sin∠??????=4
5
; ∴????=????=4
5
; 在????△??????中,????⊥????,由射影定理得: ??
??
2
=?????????,即????=??
??
2
÷????=20.
26. (1)证明:连接????; ∵∠??????=
90
°
,????为直径, ∴????为⊙??的切线; 又∵????也为⊙??的切线, ∴????=????, 又∵∠??????=
90
°
, ∴∠??????+∠??????=
90
°
, ∴∠??????+∠??=
90
°
又∵∠??+∠??=
90
°
, ∴∠??????=∠??, ∴????=????, ∴????=????,即点??是边????的中点;
/
(2)解:∵????,????分别是⊙??的切线和割线, ∴??
??
2
=?????????, ∴(2????
)
2
=?????????,即?????2
6
=36, ∴????=3
6
, 在????△??????中,由勾股定理得 ????=
??
??
2
???
??
2
=
(3
6
)
2
?
6
2
=3
2
;(3)解:△??????是等腰直角三角形. 理由:∵四边形????????为正方形, ∴∠??????=∠??????=
90
°
,即?????//?????, 又∵点??是边????的中点, ∴????=2????=????, ∴△??????是等腰直角三角形.
