25.2.2 频率与概率课时作业(1)
文档属性
| 名称 | 25.2.2 频率与概率课时作业(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-10 14:06:19 | ||
图片预览



文档简介
25.2.2 频率与概率课时作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一箱灯泡的合格率是,小刚由箱中任意买一个,则他买到次品的概率是( )
A. B. C. D.
2.在一个不透明的塑料袋中装有红色、白色球共80个,除颜色外其它都相同,小明将球搅拌均匀后,任意摸出1个球记下颜色,再放回塑料袋中,通过大量重复试验后发现,其中摸到红色球的频率稳定在30%附近,则塑料袋中白色球的个数为( )
A. 24 B. 30 C. 50 D. 56
3.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A. 概率是随机的,与频率无关 B. 频率与试验次数无关
C. 随着试验次数的增加,频率一般会越来越接近概率 D. 频率就是概率
4.如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )
A. ①② B. ②③ C. ①③ D. ①②③
5.一个密闭不透明的盒子里有若干个白球和黑球,在不允许将球倒出来的情况下,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球400次,其中80次摸到黑球,估计摸到白球的概率为( )
A. 0.4 B. 0.2 C. 0.8 D. 0.6
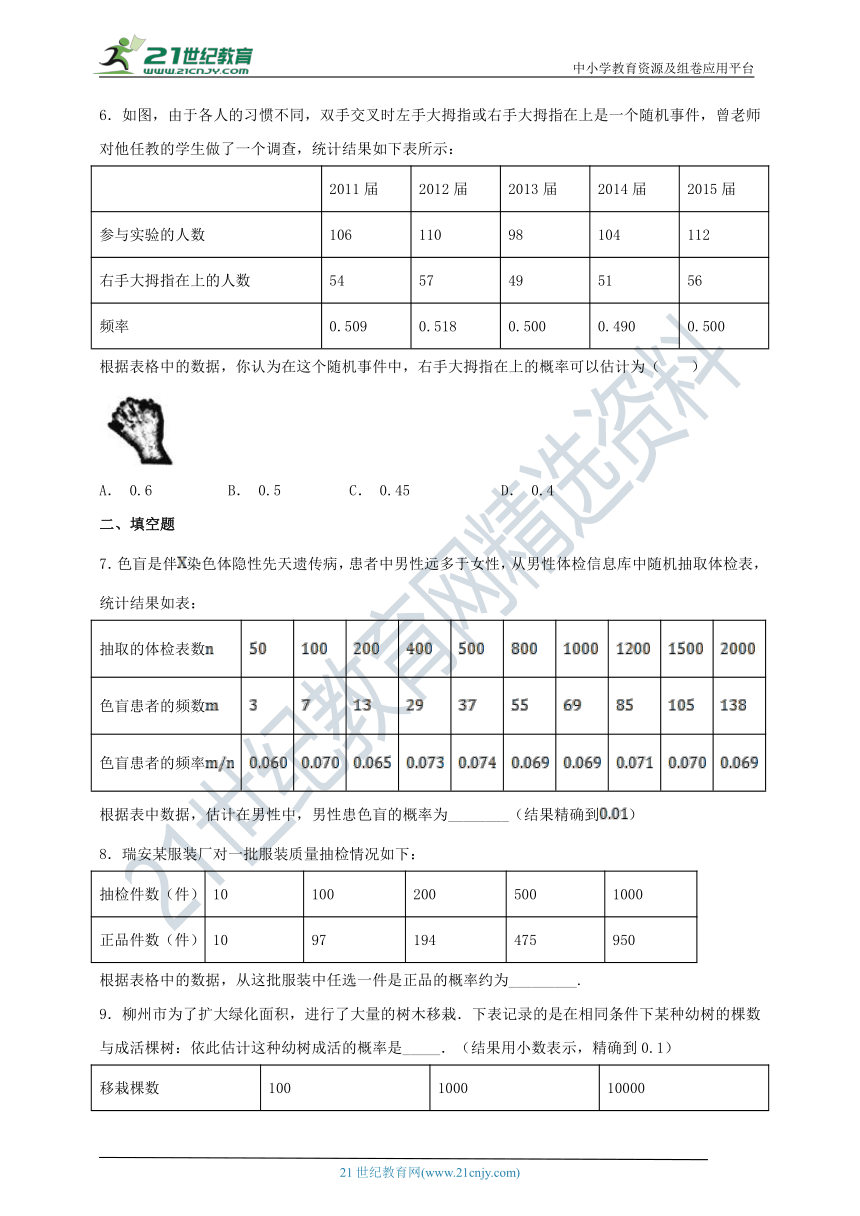
6.如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )
A. 0.6 B. 0.5 C. 0.45 D. 0.4
二、填空题
7.色盲是伴染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
抽取的体检表数
色盲患者的频数
色盲患者的频率
根据表中数据,估计在男性中,男性患色盲的概率为________(结果精确到)
8.瑞安某服装厂对一批服装质量抽检情况如下:
抽检件数(件)
10
100
200
500
1000
正品件数(件)
10
97
194
475
950
根据表格中的数据,从这批服装中任选一件是正品的概率约为_________.
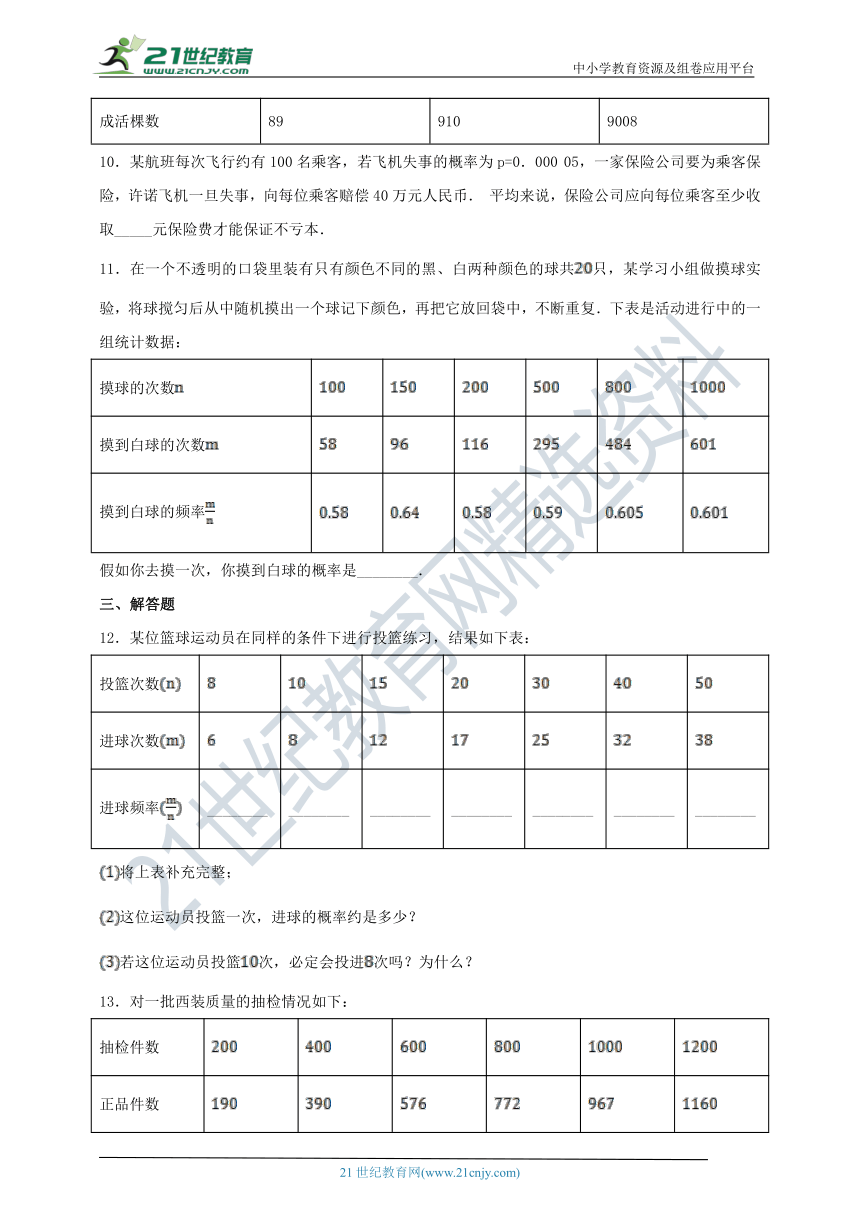
9.柳州市为了扩大绿化面积,进行了大量的树木移栽.下表记录的是在相同条件下某种幼树的棵数与成活棵树:依此估计这种幼树成活的概率是_____.(结果用小数表示,精确到0.1)
移栽棵数
100
1000
10000
成活棵数
89
910
9008
10.某航班每次飞行约有100名乘客,若飞机失事的概率为p=0.000 05,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿40万元人民币. 平均来说,保险公司应向每位乘客至少收取_____元保险费才能保证不亏本.
11.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
假如你去摸一次,你摸到白球的概率是________.
三、解答题
12.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数
进球次数
进球频率
________
________
________
________
________
________
________
将上表补充完整;
这位运动员投篮一次,进球的概率约是多少?
若这位运动员投篮次,必定会投进次吗?为什么?
13.对一批西装质量的抽检情况如下:
抽检件数
正品件数
正品的频率
________
________
________
________
________
________
填写表格中正品的频率;
从这批西装中任选一套是正品的概率是多少?
若要销售这批西装?件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装?
14.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学 习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
(1)请估计:当实验次数很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到红球的概率是 ;(精确到0.1).
(2)试估算口袋中红球有多少只?
15.在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
参考答案
1.D
【解析】
【分析】
由合格率和次品率之和为1,可得这箱灯泡次品率为1﹣87.5%=12.5%=.任买一个是次品的概率等于次品率.
【详解】
由箱中任意买一个是次品的概率为:1﹣87.5%=.
故选D.
【点睛】
本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.解答本题的关键是合格率和次品率之和为1进行计算.
2.D
【解析】
【分析】
根据频率估算出概率即可根据概率公式求出塑料袋中白色球的个数.
【详解】
∵大量重复试验后发现,其中摸到红色球的频率稳定在30%附近,
∴摸到红球的概率为30%,
∴红球的个数为:8030%=24(个)
∴白球个数为:80-24=56(个)
故选D.
【点睛】
本题考查了由频率估计概率的知识,了解大量重复实验中事件发生的频率等于事件发生的概率并熟练掌握概率公式是解题关键.
3.C
【解析】
A、概率是理论数据不是随机的,故错误;
B、随着试验次数的增加,频率一般会越来越接近概率,故错误;
C、随着试验次数的增加,频率一般会越来越接近概率,正确; D、频率不直接等于概率,故错误.
故选:C.
4.A
【解析】
【分析】
根据图形和各个小题的说法可以判断是否正确,从而可以解答本题.
【详解】
当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以这次“钉尖向上”的概率是:308÷500=0.616,故①正确.
随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618.故②正确,
若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故③错误,
故选A.
【点睛】
本题考查利用频率估计概率,解答本题的关键是明确概率的定义,利用数形结合的思想解答.
5.C
【解析】分析:共摸球400次,其中80次摸到黑球,那么有320次摸到白球;由此可知:摸到黑球与摸到白球的次数之比为80:320,由此可求摸到白球的概率.
详解:由题意可的:=0.8.
故选:C.
点睛:本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.关键是根据白球和黑球的比得到相应的关系式.
6.B
【解析】频率的平均数为:(0.509+0.518+0.500+0.490+0.500)÷5=0.5034≈0.5,
所以可以估计右手大拇指在上的概率约为0.5,
故选B.
7.
【解析】
【分析】
观察随着实验次数的增多,频率逐渐稳定到的常数即可表示男性患色盲的概率.
【详解】
观察表格发现,随着实验人数的增多,男性患色盲的频率逐渐稳定在常数0.07左右,
故男性中,男性患色盲的概率为0.07,
故答案为:0.07.
【点睛】
本题考查了利用频率估计概率的知识,解题的关键是仔细观察表格,找到频率稳定到的常数,难度不大.
8.0.95
【解析】
【分析】
用正品数分别除以抽检件数得到正品的频率.
【详解】
正品的概率=(10+97+194+475+950) ÷(10+100+200+500+1000)= 0.95.
【点睛】
本题考查的是概率计算,熟练掌握概率公式是解题的关键.
9.0.9
【解析】
【分析】
成活的总棵树除以移栽的总棵树即为所求的概率.
【详解】
根据抽样的意义可得幼树成活的概率为. 故本题答案为:0.9.
【点睛】
本题主要考查概率知识点,本题利用了用大量试验得到的频率可以估计事件的概率.用到的知识点为:概率=所求情况数与总情况数之比.
10.20
【解析】
每次约有100名乘客,如飞机一旦失事,每位乘客赔偿40万人民币,共计4000万元,由题意可得一次飞行中飞机失事的概率为P=0.00005,所以赔偿的钱数为40000000×0.00005=2000元,即可得至少应该收取保险费每人 =20元.
11.0.6
【解析】
【分析】
根据利用频率估计概率,由于摸到白球的频率稳定在0.6左右,由此可估计摸到白球的概率为0.6.
【详解】
根据摸到白球的频率稳定在0.6左右,所以摸一次,摸到白球的概率为0.6.
故答案为:0.6.
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
12.答案为:;;;;;;;;这位运动员投篮次,不一定会投进次,理由详见解析.
【解析】
【分析】
(1)根据进球频率=进球次数与投篮次数的比进行补充即可;(2)根据进球频率即可估计出进球的概率,所计算的频率都在0.8左右波动,所以可估计进球的概率约是0.8;(3)根据概率的意义进行回答即可.
【详解】
答案为:;;;;;;;这位运动员投篮一次,进球的概率约是;若这位运动员投篮次,不一定会投进次.因为进球的概率是是通过大量重复实验得到的,而投篮次是随机的,所以不一定会投进次,也可能都不进,也可能都进.
【点睛】
本题考查了利用概率估计频率:当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.
13.;;;;;;;件.
【解析】
【分析】
(1)用正品数分别除以抽检件数得到正品的频率; (2)根据(1)的计算可估计任选一套是正品的概率为0.976; (3)同2000件除以正品的概率即可.
【详解】
解:答案为:;;;;;;
从这批西装中任选一套是正品的概率是;
为了方便购买次品西装的顾客前来调换,所进西装的件数(件).
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
14.(1)0.3 ,0.7;(2)70.
【解析】试题分析:(1)从表中的统计数据可知,摸到白球的频率稳定在0.3左右,而摸到红球的概率为1-0.3=0.7;(2)根据红球的概率公式得到相应方程求解即可;(3)言之有理即可.
试题解析:(1)0.3, 0.3;
(2)估算口袋中红球有x只,
由题意得0.7=,
解之得x=70,
∴估计口袋中红球有70只;
(3)用概率可以估计未知物体的数目.(或者试验次数很大时事件发生的频率作为概率的近似值)
15.(1)估计盒子里白球个数约为20个,黑球个数为20个;(2)需要往盒子里再放入20个白球.
【解析】
【分析】
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近,所以摸到白球的概率为,据此用球的总个数乘以白球概率可得白球数量,继而可得答案;
(2)设需要往盒子里再放入个白球,根据题意得出方程,解方程即可.
【详解】
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近0.50,
所以摸到白球的概率为0.5,
估计盒子里白球个数约为40×0.5=20个,黑球个数为40﹣20=20个;
(2)设需要往盒子里再放入x个白球;
根据题意得: =,
解得:x=20;
答:需要往盒子里再放入20个白球.
【点睛】
本题考查了利用频率估计概率、概率公式的运用,大量反复试验下频率稳定值即概率,本题难度适中.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一箱灯泡的合格率是,小刚由箱中任意买一个,则他买到次品的概率是( )
A. B. C. D.
2.在一个不透明的塑料袋中装有红色、白色球共80个,除颜色外其它都相同,小明将球搅拌均匀后,任意摸出1个球记下颜色,再放回塑料袋中,通过大量重复试验后发现,其中摸到红色球的频率稳定在30%附近,则塑料袋中白色球的个数为( )
A. 24 B. 30 C. 50 D. 56
3.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A. 概率是随机的,与频率无关 B. 频率与试验次数无关
C. 随着试验次数的增加,频率一般会越来越接近概率 D. 频率就是概率
4.如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )
A. ①② B. ②③ C. ①③ D. ①②③
5.一个密闭不透明的盒子里有若干个白球和黑球,在不允许将球倒出来的情况下,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球400次,其中80次摸到黑球,估计摸到白球的概率为( )
A. 0.4 B. 0.2 C. 0.8 D. 0.6
6.如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )
A. 0.6 B. 0.5 C. 0.45 D. 0.4
二、填空题
7.色盲是伴染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
抽取的体检表数
色盲患者的频数
色盲患者的频率
根据表中数据,估计在男性中,男性患色盲的概率为________(结果精确到)
8.瑞安某服装厂对一批服装质量抽检情况如下:
抽检件数(件)
10
100
200
500
1000
正品件数(件)
10
97
194
475
950
根据表格中的数据,从这批服装中任选一件是正品的概率约为_________.
9.柳州市为了扩大绿化面积,进行了大量的树木移栽.下表记录的是在相同条件下某种幼树的棵数与成活棵树:依此估计这种幼树成活的概率是_____.(结果用小数表示,精确到0.1)
移栽棵数
100
1000
10000
成活棵数
89
910
9008
10.某航班每次飞行约有100名乘客,若飞机失事的概率为p=0.000 05,一家保险公司要为乘客保险,许诺飞机一旦失事,向每位乘客赔偿40万元人民币. 平均来说,保险公司应向每位乘客至少收取_____元保险费才能保证不亏本.
11.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
假如你去摸一次,你摸到白球的概率是________.
三、解答题
12.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数
进球次数
进球频率
________
________
________
________
________
________
________
将上表补充完整;
这位运动员投篮一次,进球的概率约是多少?
若这位运动员投篮次,必定会投进次吗?为什么?
13.对一批西装质量的抽检情况如下:
抽检件数
正品件数
正品的频率
________
________
________
________
________
________
填写表格中正品的频率;
从这批西装中任选一套是正品的概率是多少?
若要销售这批西装?件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装?
14.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学 习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
(1)请估计:当实验次数很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到红球的概率是 ;(精确到0.1).
(2)试估算口袋中红球有多少只?
15.在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
参考答案
1.D
【解析】
【分析】
由合格率和次品率之和为1,可得这箱灯泡次品率为1﹣87.5%=12.5%=.任买一个是次品的概率等于次品率.
【详解】
由箱中任意买一个是次品的概率为:1﹣87.5%=.
故选D.
【点睛】
本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.解答本题的关键是合格率和次品率之和为1进行计算.
2.D
【解析】
【分析】
根据频率估算出概率即可根据概率公式求出塑料袋中白色球的个数.
【详解】
∵大量重复试验后发现,其中摸到红色球的频率稳定在30%附近,
∴摸到红球的概率为30%,
∴红球的个数为:8030%=24(个)
∴白球个数为:80-24=56(个)
故选D.
【点睛】
本题考查了由频率估计概率的知识,了解大量重复实验中事件发生的频率等于事件发生的概率并熟练掌握概率公式是解题关键.
3.C
【解析】
A、概率是理论数据不是随机的,故错误;
B、随着试验次数的增加,频率一般会越来越接近概率,故错误;
C、随着试验次数的增加,频率一般会越来越接近概率,正确; D、频率不直接等于概率,故错误.
故选:C.
4.A
【解析】
【分析】
根据图形和各个小题的说法可以判断是否正确,从而可以解答本题.
【详解】
当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以这次“钉尖向上”的概率是:308÷500=0.616,故①正确.
随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618.故②正确,
若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率可能是0.620,但不一定是0.620,故③错误,
故选A.
【点睛】
本题考查利用频率估计概率,解答本题的关键是明确概率的定义,利用数形结合的思想解答.
5.C
【解析】分析:共摸球400次,其中80次摸到黑球,那么有320次摸到白球;由此可知:摸到黑球与摸到白球的次数之比为80:320,由此可求摸到白球的概率.
详解:由题意可的:=0.8.
故选:C.
点睛:本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.关键是根据白球和黑球的比得到相应的关系式.
6.B
【解析】频率的平均数为:(0.509+0.518+0.500+0.490+0.500)÷5=0.5034≈0.5,
所以可以估计右手大拇指在上的概率约为0.5,
故选B.
7.
【解析】
【分析】
观察随着实验次数的增多,频率逐渐稳定到的常数即可表示男性患色盲的概率.
【详解】
观察表格发现,随着实验人数的增多,男性患色盲的频率逐渐稳定在常数0.07左右,
故男性中,男性患色盲的概率为0.07,
故答案为:0.07.
【点睛】
本题考查了利用频率估计概率的知识,解题的关键是仔细观察表格,找到频率稳定到的常数,难度不大.
8.0.95
【解析】
【分析】
用正品数分别除以抽检件数得到正品的频率.
【详解】
正品的概率=(10+97+194+475+950) ÷(10+100+200+500+1000)= 0.95.
【点睛】
本题考查的是概率计算,熟练掌握概率公式是解题的关键.
9.0.9
【解析】
【分析】
成活的总棵树除以移栽的总棵树即为所求的概率.
【详解】
根据抽样的意义可得幼树成活的概率为. 故本题答案为:0.9.
【点睛】
本题主要考查概率知识点,本题利用了用大量试验得到的频率可以估计事件的概率.用到的知识点为:概率=所求情况数与总情况数之比.
10.20
【解析】
每次约有100名乘客,如飞机一旦失事,每位乘客赔偿40万人民币,共计4000万元,由题意可得一次飞行中飞机失事的概率为P=0.00005,所以赔偿的钱数为40000000×0.00005=2000元,即可得至少应该收取保险费每人 =20元.
11.0.6
【解析】
【分析】
根据利用频率估计概率,由于摸到白球的频率稳定在0.6左右,由此可估计摸到白球的概率为0.6.
【详解】
根据摸到白球的频率稳定在0.6左右,所以摸一次,摸到白球的概率为0.6.
故答案为:0.6.
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
12.答案为:;;;;;;;;这位运动员投篮次,不一定会投进次,理由详见解析.
【解析】
【分析】
(1)根据进球频率=进球次数与投篮次数的比进行补充即可;(2)根据进球频率即可估计出进球的概率,所计算的频率都在0.8左右波动,所以可估计进球的概率约是0.8;(3)根据概率的意义进行回答即可.
【详解】
答案为:;;;;;;;这位运动员投篮一次,进球的概率约是;若这位运动员投篮次,不一定会投进次.因为进球的概率是是通过大量重复实验得到的,而投篮次是随机的,所以不一定会投进次,也可能都不进,也可能都进.
【点睛】
本题考查了利用概率估计频率:当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.
13.;;;;;;;件.
【解析】
【分析】
(1)用正品数分别除以抽检件数得到正品的频率; (2)根据(1)的计算可估计任选一套是正品的概率为0.976; (3)同2000件除以正品的概率即可.
【详解】
解:答案为:;;;;;;
从这批西装中任选一套是正品的概率是;
为了方便购买次品西装的顾客前来调换,所进西装的件数(件).
【点睛】
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
14.(1)0.3 ,0.7;(2)70.
【解析】试题分析:(1)从表中的统计数据可知,摸到白球的频率稳定在0.3左右,而摸到红球的概率为1-0.3=0.7;(2)根据红球的概率公式得到相应方程求解即可;(3)言之有理即可.
试题解析:(1)0.3, 0.3;
(2)估算口袋中红球有x只,
由题意得0.7=,
解之得x=70,
∴估计口袋中红球有70只;
(3)用概率可以估计未知物体的数目.(或者试验次数很大时事件发生的频率作为概率的近似值)
15.(1)估计盒子里白球个数约为20个,黑球个数为20个;(2)需要往盒子里再放入20个白球.
【解析】
【分析】
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近,所以摸到白球的概率为,据此用球的总个数乘以白球概率可得白球数量,继而可得答案;
(2)设需要往盒子里再放入个白球,根据题意得出方程,解方程即可.
【详解】
(1)由折线统计图知,当摸球次数很大时,摸到白球的概率将会接近0.50,
所以摸到白球的概率为0.5,
估计盒子里白球个数约为40×0.5=20个,黑球个数为40﹣20=20个;
(2)设需要往盒子里再放入x个白球;
根据题意得: =,
解得:x=20;
答:需要往盒子里再放入20个白球.
【点睛】
本题考查了利用频率估计概率、概率公式的运用,大量反复试验下频率稳定值即概率,本题难度适中.
