1.4 解直角三角形复习题-解答题(含解析)
文档属性
| 名称 | 1.4 解直角三角形复习题-解答题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-11 10:20:50 | ||
图片预览



文档简介
第一章 直角三角形的边角关系复习题解答题
一.解答题
1.(2018?贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
2.(2018?赤峰)阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c?sinB
∴S△ABC=a?AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
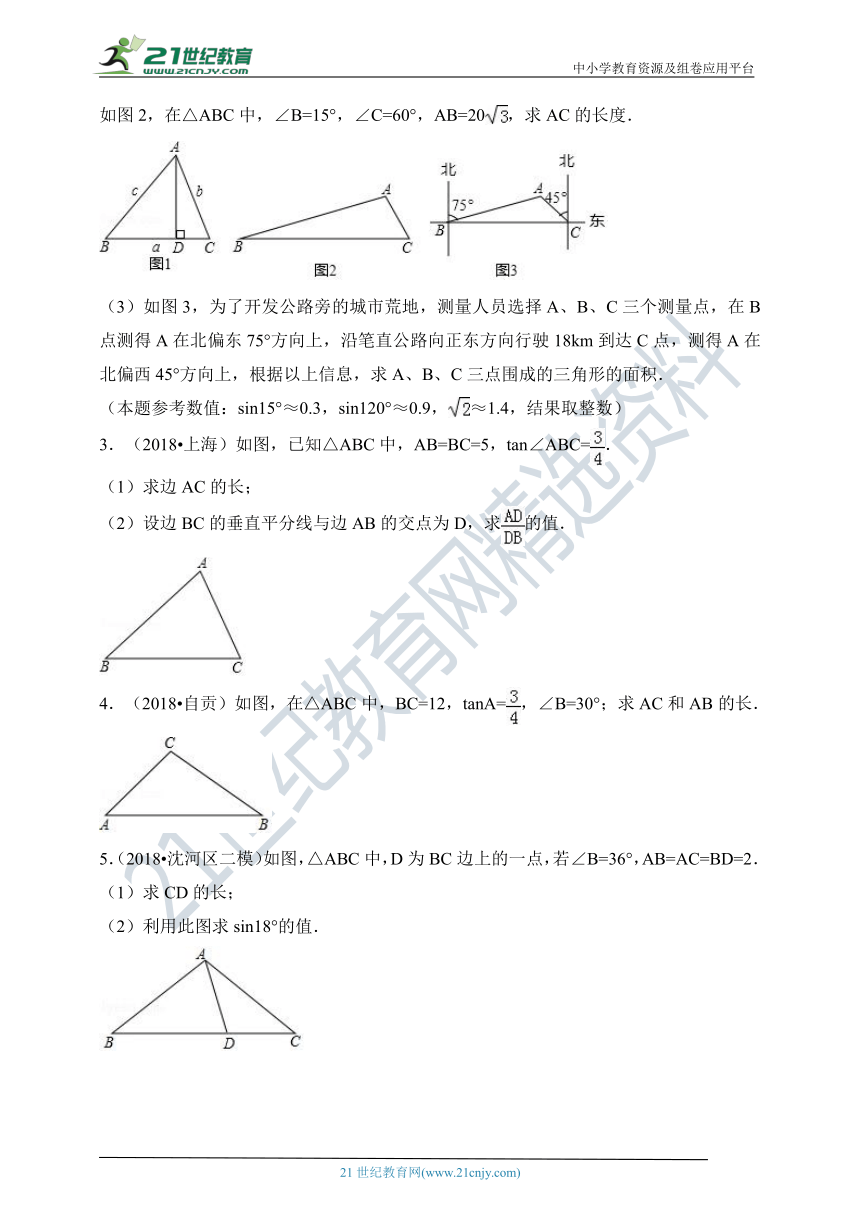
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
3.(2018?上海)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
4.(2018?自贡)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
5.(2018?沈河区二模)如图,△ABC中,D为BC边上的一点,若∠B=36°,AB=AC=BD=2.
(1)求CD的长;
(2)利用此图求sin18°的值.
6.(2018?张店区一模)如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=,求CB的长.
7.(2018?相山区四模)如图,在△ABC中,∠B为锐角,AB=3,AC=5,sinC=,求BC的长.
8.(2018?淮南模拟)在平面直角坐标系中,若△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,3),C(﹣4,3),求sinB的值.
9.(2018?合肥模拟)如图,在△ABC中,∠B=45°,∠C=60°,AC=20.
(1)求BC的长度;
(2)若∠ADC=75°,求CD的长.
10.(2018?西城区一模)如图,在△ABD中,∠ABD=∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,分别连接BC,DC,AC,记AC与BD的交点为O.
(1)补全图形,求∠AOB的度数并说明理由;
(2)若AB=5,cos∠ABD=,求BD的长.
11.(2018?绥化模拟)如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
(1)求证:BC=2AD;
(2)若cosB=,AB=10,求CD的长.
12.(2018?松江区二模)如图,已知△ABC中,∠B=45°,tanC=,BC=6.
(1)求△ABC面积;
(2)AC的垂直平分线交AC于点D,交BC于点E.求DE的长.
13.(2018?沙湾区模拟)阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
14.(2018?大庆模拟)对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cos=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个直角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
第一章 直角三角形的边角关系复习题解答题
参考答案与试题解析
一.解答题(共14小题)
1.(2018?贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
【分析】三式相等,理由为:过A作AD⊥BC,BE⊥AC,在直角三角形ABD中,利用锐角三角函数定义表示出AD,在直角三角形ADC中,利用锐角三角函数定义表示出AD,两者相等即可得证.
【解答】解:==,理由为:
过A作AD⊥BC,BE⊥AC,
在Rt△ABD中,sinB=,即AD=csinB,
在Rt△ADC中,sinC=,即AD=bsinC,
∴csinB=bsinC,即=,
同理可得=,
则==.
2.(2018?赤峰)阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c?sinB
∴S△ABC=a?AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
【分析】(1)根据材料中的S△ABC=absinC=acsinB=bcsinA,化为比例式可得结论;
(2)根据公式,直接代入可得结论;
(3)先根据公式计算AC的长,由S△ABC=AC×BC×sin∠ACB可得结论.
【解答】解:(1)∵absinC=acsinB,
∴bsinC=csinB,
∴=,
:同理得:=,
∴==;(4分)
(2)由题意得:∠B=15°,∠C=60°,AB=20,
∴,即,
∴,
∴AC=40×0.3=12;(8分)
(3)由题意得:∠ABC=90°﹣75°=15°,∠ACB=90°﹣45°=45°,
∠A=180°﹣15°﹣45°=120°,
由==得:=,
∴AC=6,
∴S△ABC=AC×BC×sin∠ACB=×6×18×0.7≈38.(12分)
3.(2018?上海)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
权所有
【分析】(1)过A作AE⊥BC,在直角三角形ABE中,利用锐角三角函数定义求出AC的长即可;
(2)由DF垂直平分BC,求出BF的长,利用锐角三角函数定义求出DF的长,利用勾股定理求出BD的长,进而求出AD的长,即可求出所求.
【解答】解:(1)作A作AE⊥BC,
在Rt△ABE中,tan∠ABC==,AB=5,
∴AE=3,BE=4,
∴CE=BC﹣BE=5﹣4=1,
在Rt△AEC中,根据勾股定理得:AC==;
(2)∵DF垂直平分BC,
∴BD=CD,BF=CF=,
∵tan∠DBF==,
∴DF=,
在Rt△BFD中,根据勾股定理得:BD==,
∴AD=5﹣=,
则=.
4.(2018?自贡)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
【分析】如图作CH⊥AB于H.在Rt△求出CH、BH,这种Rt△ACH中求出AH、AC即可解决问题;
【解答】解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,
∴AH=8,
∴AC==10,
∴AB=AH+BH=8+6.
5.(2018?沈河区二模)如图,△ABC中,D为BC边上的一点,若∠B=36°,AB=AC=BD=2.
(1)求CD的长;
(2)利用此图求sin18°的值.
【分析】(1)求出△CAD∽△CBA,得出比例式,代入求出即可;
(2)求出△EAD是直角三角形,求出AD的长度,即可求出答案.
【解答】解:(1)∵AB=AC,∠B=36°,
∴∠C=∠B=36°,
∴∠BAC=180°﹣∠B﹣∠C=108°,
∵AB=BD,∠B=36°,
∴∠BAD=∠BDA=(180°﹣∠B)=72°,
∴∠CAD=∠BAC﹣∠BAD=108°﹣72°=36°,
即∠DAC=∠B,
∵∠C=∠C,
∴△CAD∽△CBA,
∴=,
∵AB=AC=BD=2,
∴=,
解得:CD=﹣1(负数舍去);
(2)
延长CB到E,使BE=AB=2,连接AE,
则∠E=∠BAE,
∵∠ABC=36°=∠E+∠BAE,
∴∠E=∠BAE=18°,
∵∠BAD=72°,
∴∠EAD=72°+18°=90°,
∵∠C=∠CAD=36°,
∴AD=CD=﹣1,
在Rt△EAD中,sinE===,
即sin18°=.
6.(2018?张店区一模)如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=,求CB的长.
【分析】(1)根据平行四边形的判定定理(有一组对边平行且相等的四边形是平四边形)推知四边形ACC'A'是平行四边形.有一组邻边相等的平行四边形是菱形推知四边形ACC'A'是菱形.
(2)通过解直角△ABC得到AC的长,利用勾股定理即可得到BC的长度.
【解答】解:(1)四边形ACC'A'是菱形.理由如下:
由平移的性质得到:AC∥A′C′,且AC=A′C′,
则四边形ACC'A'是平行四边形.
又∵CD平分∠ACB的外角,
∴∠ACA′=∠A'CC',
∵AA'∥BB',
∴∠C'CA'=∠AA'C,
∴∠AA'C=∠ACA',
∴AA'=AC,
∴四边形ACC'A'是菱形.
(2)∵在△ABC中,∠B=90°,AB=24,cos∠BAC=,
∴cos∠BAC==,即=,
∴AC=26.
∴由勾股定理知:BC===10.
7.(2018?相山区四模)如图,在△ABC中,∠B为锐角,AB=3,AC=5,sinC=,求BC的长.
【分析】作AD⊥BC,在△ACD中求得AD=ACsinC=3、,再在△ABD中根据AB=3、AD=3求得BD=3,继而根据BC=BD+CD可得答案.
【解答】解:作AD⊥BC于点D,
∴∠ADB=∠ADC=90°.
∵AC=5,,
∴AD=AC?sinC=3.
∴在Rt△ACD中,.
∵AB=,
∴在Rt△ABD中,.
∴BC=BD+CD=7.
8.(2018?淮南模拟)在平面直角坐标系中,若△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,3),C(﹣4,3),求sinB的值.
【分析】根据平面坐标系得出各点坐标,进而得出,△ABC是直角三角形,进而得出sinB的值.
【解答】解:如图所示:AC=2,BC=3,由勾股定理得:
AB=,
sinB=.
9.(2018?合肥模拟)如图,在△ABC中,∠B=45°,∠C=60°,AC=20.
(1)求BC的长度;
(2)若∠ADC=75°,求CD的长.
【分析】(1)作AE⊥BC于E,如图,在Rt△ACE中利用∠C=60°可计算出CE=10,AE=10,在Rt△ABE中利用∠B=45°得到BE=AE=10,从而得到BC的长;
(2)证明△CDA∽△CAB,然后利用相似比计算CD的长.
【解答】解:(1)作AE⊥BC于E,如图,
在Rt△ACE中,∵∠C=60°,
∴CE=AC=10,AE=CE=10,
在Rt△ABE中,∵∠B=45°,
∴BE=AE=10,
∴BC=BE+CE=10+10;
(2)∵∠BAC=180°﹣45°﹣60°=75°,
而∠ADC=75°,
∴∠ADC=∠ABC,
∵∠ACD=∠BCA,
∴△CDA∽△CAB,
∴=,即=,
∴CD=20﹣20.
10.(2018?西城区一模)如图,在△ABD中,∠ABD=∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,分别连接BC,DC,AC,记AC与BD的交点为O.
(1)补全图形,求∠AOB的度数并说明理由;
(2)若AB=5,cos∠ABD=,求BD的长.
权所有
【分析】(1)补全图形,如图所示,可得出∠AOB=90°,理由如下:由题意得到四边形为菱形,利用菱形的性质判断即可;
(2)在直角三角形AOB中,利用锐角三角函数定义求出BO的长,由BD=2BO即可求出BD的长.
【解答】解:(1)补全的图形,如图所示,可得出∠AOB=90°,理由如下:
证明:由题意可知BC=AB,DC=AB,
∵在△ABD中,∠ABD=∠ADB,
∴AB=AD,
∴BC=DC=AD=AB,
∴四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOB=90°;
(2)∵四边形ABCD为菱形,
∴OB=OD.
在Rt△ABO中,∠AOB=90°,AB=5,cos∠ABD=,
∴OB=AB?cos∠ABD=3,
∴BD=2OB=6.
11.(2018?绥化模拟)如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
(1)求证:BC=2AD;
(2)若cosB=,AB=10,求CD的长.
【分析】(1)由tanA=2cos∠BCD即可求得结论;
(2)由∠B的余弦值和(1)的结论即可求得BD,利用勾股定理求得CD.
【解答】解:(1)∵tanA=,cos∠BCD=,tanA=2cos∠BCD,
∴=2×,
∴BC=2AD;
(2)∵cosB==,BC=2AD,
∴=,
∵AB=10,
∴AD=×10=4,BD=10﹣4=6,
∴BC=8,
∴CD==2.
12.(2018?松江区二模)如图,已知△ABC中,∠B=45°,tanC=,BC=6.
(1)求△ABC面积;
(2)AC的垂直平分线交AC于点D,交BC于点E.求DE的长.
【分析】(1)过点A作AH⊥BC于点H,根据题意得到三角形ACH为等腰直角三角形,设AH=BH=x,根据tanC的值,表示出HC,由BC=6求出x的值,确定出AH的长,即可求出三角形ABC面积;
(2)由(1)得到AH与CH的长,利用勾股定理求出AC的长,进而确定出CD的长,根据tanC的值,利用锐角三角函数定义求出DE的长即可.
【解答】解:(1)过点A作AH⊥BC于点H,
在Rt△ABC中,∠B=45°,
设AH=x,则BH=x,
在Rt△AHC中,tanC==,
∴HC=2x,
∵BC=6,
∴x+2x=6,
解得:x=2,
∴AH=2,
∴S△ABC=?BC?AH=6;
(2)由(1)得AH=2,CH=4,
在Rt△AHC中,AC==2,
∵DE垂直平分AC,
∴CD=AC=,
∵ED⊥AC,
∴在Rt△EDC中,tanC==,
∴DE=.
13.(2018?沙湾区模拟)阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
【分析】(1)解直角三角形求出cosA,利用结论中的公式计算即可;
(2)利用图2,根据cos2A=cos∠CED=,计算即可;
【解答】解:(1)如图3中,在Rt△ABC中,∵AB=3,BC=1,∠C=90°,
∴AC==2,
∴sinA==,cosA=,
∴sinA=2cosA?sinA=
(2)如图2中,cos2A=cos∠CED===2AC?cosA﹣1=2(cosA)2﹣1.
14.(2018?大庆模拟)对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cos=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个直角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
【分析】(1)仿照已知定义将各式变形,利用特殊角的三角函数值求出值即可;
(2)根据内角之比,利用内角和为180°求出各自的度数,根据sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求出m的值,进而确定出∠A和∠B的度数.
【解答】解:(1)由题意得:sin120°=sin(180°﹣120°)=sin60°=,cos150°=cos(180°﹣30°)=﹣cos30°=﹣;
(2)∵一个直角三角形的三个内角比是1:1:4,
∴三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为,﹣,
把代入方程得:1﹣m﹣1=0,解得:m=0,
经检验﹣是4x2﹣1=0的根,故m=0;
②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;
③∠A=30°,∠B=30°时,方程两根为,,
把代入得:1﹣m﹣1=0,解得:m=0,
经检验不是方程4x2﹣1=0的根,不符合题意,
则m=0,∠A=30°,∠B=120°.
一.解答题
1.(2018?贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
2.(2018?赤峰)阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c?sinB
∴S△ABC=a?AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
3.(2018?上海)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
4.(2018?自贡)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
5.(2018?沈河区二模)如图,△ABC中,D为BC边上的一点,若∠B=36°,AB=AC=BD=2.
(1)求CD的长;
(2)利用此图求sin18°的值.
6.(2018?张店区一模)如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=,求CB的长.
7.(2018?相山区四模)如图,在△ABC中,∠B为锐角,AB=3,AC=5,sinC=,求BC的长.
8.(2018?淮南模拟)在平面直角坐标系中,若△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,3),C(﹣4,3),求sinB的值.
9.(2018?合肥模拟)如图,在△ABC中,∠B=45°,∠C=60°,AC=20.
(1)求BC的长度;
(2)若∠ADC=75°,求CD的长.
10.(2018?西城区一模)如图,在△ABD中,∠ABD=∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,分别连接BC,DC,AC,记AC与BD的交点为O.
(1)补全图形,求∠AOB的度数并说明理由;
(2)若AB=5,cos∠ABD=,求BD的长.
11.(2018?绥化模拟)如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
(1)求证:BC=2AD;
(2)若cosB=,AB=10,求CD的长.
12.(2018?松江区二模)如图,已知△ABC中,∠B=45°,tanC=,BC=6.
(1)求△ABC面积;
(2)AC的垂直平分线交AC于点D,交BC于点E.求DE的长.
13.(2018?沙湾区模拟)阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
14.(2018?大庆模拟)对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cos=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个直角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
第一章 直角三角形的边角关系复习题解答题
参考答案与试题解析
一.解答题(共14小题)
1.(2018?贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
【分析】三式相等,理由为:过A作AD⊥BC,BE⊥AC,在直角三角形ABD中,利用锐角三角函数定义表示出AD,在直角三角形ADC中,利用锐角三角函数定义表示出AD,两者相等即可得证.
【解答】解:==,理由为:
过A作AD⊥BC,BE⊥AC,
在Rt△ABD中,sinB=,即AD=csinB,
在Rt△ADC中,sinC=,即AD=bsinC,
∴csinB=bsinC,即=,
同理可得=,
则==.
2.(2018?赤峰)阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c?sinB
∴S△ABC=a?AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
【分析】(1)根据材料中的S△ABC=absinC=acsinB=bcsinA,化为比例式可得结论;
(2)根据公式,直接代入可得结论;
(3)先根据公式计算AC的长,由S△ABC=AC×BC×sin∠ACB可得结论.
【解答】解:(1)∵absinC=acsinB,
∴bsinC=csinB,
∴=,
:同理得:=,
∴==;(4分)
(2)由题意得:∠B=15°,∠C=60°,AB=20,
∴,即,
∴,
∴AC=40×0.3=12;(8分)
(3)由题意得:∠ABC=90°﹣75°=15°,∠ACB=90°﹣45°=45°,
∠A=180°﹣15°﹣45°=120°,
由==得:=,
∴AC=6,
∴S△ABC=AC×BC×sin∠ACB=×6×18×0.7≈38.(12分)
3.(2018?上海)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
权所有
【分析】(1)过A作AE⊥BC,在直角三角形ABE中,利用锐角三角函数定义求出AC的长即可;
(2)由DF垂直平分BC,求出BF的长,利用锐角三角函数定义求出DF的长,利用勾股定理求出BD的长,进而求出AD的长,即可求出所求.
【解答】解:(1)作A作AE⊥BC,
在Rt△ABE中,tan∠ABC==,AB=5,
∴AE=3,BE=4,
∴CE=BC﹣BE=5﹣4=1,
在Rt△AEC中,根据勾股定理得:AC==;
(2)∵DF垂直平分BC,
∴BD=CD,BF=CF=,
∵tan∠DBF==,
∴DF=,
在Rt△BFD中,根据勾股定理得:BD==,
∴AD=5﹣=,
则=.
4.(2018?自贡)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
【分析】如图作CH⊥AB于H.在Rt△求出CH、BH,这种Rt△ACH中求出AH、AC即可解决问题;
【解答】解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,
∴AH=8,
∴AC==10,
∴AB=AH+BH=8+6.
5.(2018?沈河区二模)如图,△ABC中,D为BC边上的一点,若∠B=36°,AB=AC=BD=2.
(1)求CD的长;
(2)利用此图求sin18°的值.
【分析】(1)求出△CAD∽△CBA,得出比例式,代入求出即可;
(2)求出△EAD是直角三角形,求出AD的长度,即可求出答案.
【解答】解:(1)∵AB=AC,∠B=36°,
∴∠C=∠B=36°,
∴∠BAC=180°﹣∠B﹣∠C=108°,
∵AB=BD,∠B=36°,
∴∠BAD=∠BDA=(180°﹣∠B)=72°,
∴∠CAD=∠BAC﹣∠BAD=108°﹣72°=36°,
即∠DAC=∠B,
∵∠C=∠C,
∴△CAD∽△CBA,
∴=,
∵AB=AC=BD=2,
∴=,
解得:CD=﹣1(负数舍去);
(2)
延长CB到E,使BE=AB=2,连接AE,
则∠E=∠BAE,
∵∠ABC=36°=∠E+∠BAE,
∴∠E=∠BAE=18°,
∵∠BAD=72°,
∴∠EAD=72°+18°=90°,
∵∠C=∠CAD=36°,
∴AD=CD=﹣1,
在Rt△EAD中,sinE===,
即sin18°=.
6.(2018?张店区一模)如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=,求CB的长.
【分析】(1)根据平行四边形的判定定理(有一组对边平行且相等的四边形是平四边形)推知四边形ACC'A'是平行四边形.有一组邻边相等的平行四边形是菱形推知四边形ACC'A'是菱形.
(2)通过解直角△ABC得到AC的长,利用勾股定理即可得到BC的长度.
【解答】解:(1)四边形ACC'A'是菱形.理由如下:
由平移的性质得到:AC∥A′C′,且AC=A′C′,
则四边形ACC'A'是平行四边形.
又∵CD平分∠ACB的外角,
∴∠ACA′=∠A'CC',
∵AA'∥BB',
∴∠C'CA'=∠AA'C,
∴∠AA'C=∠ACA',
∴AA'=AC,
∴四边形ACC'A'是菱形.
(2)∵在△ABC中,∠B=90°,AB=24,cos∠BAC=,
∴cos∠BAC==,即=,
∴AC=26.
∴由勾股定理知:BC===10.
7.(2018?相山区四模)如图,在△ABC中,∠B为锐角,AB=3,AC=5,sinC=,求BC的长.
【分析】作AD⊥BC,在△ACD中求得AD=ACsinC=3、,再在△ABD中根据AB=3、AD=3求得BD=3,继而根据BC=BD+CD可得答案.
【解答】解:作AD⊥BC于点D,
∴∠ADB=∠ADC=90°.
∵AC=5,,
∴AD=AC?sinC=3.
∴在Rt△ACD中,.
∵AB=,
∴在Rt△ABD中,.
∴BC=BD+CD=7.
8.(2018?淮南模拟)在平面直角坐标系中,若△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,3),C(﹣4,3),求sinB的值.
【分析】根据平面坐标系得出各点坐标,进而得出,△ABC是直角三角形,进而得出sinB的值.
【解答】解:如图所示:AC=2,BC=3,由勾股定理得:
AB=,
sinB=.
9.(2018?合肥模拟)如图,在△ABC中,∠B=45°,∠C=60°,AC=20.
(1)求BC的长度;
(2)若∠ADC=75°,求CD的长.
【分析】(1)作AE⊥BC于E,如图,在Rt△ACE中利用∠C=60°可计算出CE=10,AE=10,在Rt△ABE中利用∠B=45°得到BE=AE=10,从而得到BC的长;
(2)证明△CDA∽△CAB,然后利用相似比计算CD的长.
【解答】解:(1)作AE⊥BC于E,如图,
在Rt△ACE中,∵∠C=60°,
∴CE=AC=10,AE=CE=10,
在Rt△ABE中,∵∠B=45°,
∴BE=AE=10,
∴BC=BE+CE=10+10;
(2)∵∠BAC=180°﹣45°﹣60°=75°,
而∠ADC=75°,
∴∠ADC=∠ABC,
∵∠ACD=∠BCA,
∴△CDA∽△CAB,
∴=,即=,
∴CD=20﹣20.
10.(2018?西城区一模)如图,在△ABD中,∠ABD=∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,分别连接BC,DC,AC,记AC与BD的交点为O.
(1)补全图形,求∠AOB的度数并说明理由;
(2)若AB=5,cos∠ABD=,求BD的长.
权所有
【分析】(1)补全图形,如图所示,可得出∠AOB=90°,理由如下:由题意得到四边形为菱形,利用菱形的性质判断即可;
(2)在直角三角形AOB中,利用锐角三角函数定义求出BO的长,由BD=2BO即可求出BD的长.
【解答】解:(1)补全的图形,如图所示,可得出∠AOB=90°,理由如下:
证明:由题意可知BC=AB,DC=AB,
∵在△ABD中,∠ABD=∠ADB,
∴AB=AD,
∴BC=DC=AD=AB,
∴四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOB=90°;
(2)∵四边形ABCD为菱形,
∴OB=OD.
在Rt△ABO中,∠AOB=90°,AB=5,cos∠ABD=,
∴OB=AB?cos∠ABD=3,
∴BD=2OB=6.
11.(2018?绥化模拟)如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
(1)求证:BC=2AD;
(2)若cosB=,AB=10,求CD的长.
【分析】(1)由tanA=2cos∠BCD即可求得结论;
(2)由∠B的余弦值和(1)的结论即可求得BD,利用勾股定理求得CD.
【解答】解:(1)∵tanA=,cos∠BCD=,tanA=2cos∠BCD,
∴=2×,
∴BC=2AD;
(2)∵cosB==,BC=2AD,
∴=,
∵AB=10,
∴AD=×10=4,BD=10﹣4=6,
∴BC=8,
∴CD==2.
12.(2018?松江区二模)如图,已知△ABC中,∠B=45°,tanC=,BC=6.
(1)求△ABC面积;
(2)AC的垂直平分线交AC于点D,交BC于点E.求DE的长.
【分析】(1)过点A作AH⊥BC于点H,根据题意得到三角形ACH为等腰直角三角形,设AH=BH=x,根据tanC的值,表示出HC,由BC=6求出x的值,确定出AH的长,即可求出三角形ABC面积;
(2)由(1)得到AH与CH的长,利用勾股定理求出AC的长,进而确定出CD的长,根据tanC的值,利用锐角三角函数定义求出DE的长即可.
【解答】解:(1)过点A作AH⊥BC于点H,
在Rt△ABC中,∠B=45°,
设AH=x,则BH=x,
在Rt△AHC中,tanC==,
∴HC=2x,
∵BC=6,
∴x+2x=6,
解得:x=2,
∴AH=2,
∴S△ABC=?BC?AH=6;
(2)由(1)得AH=2,CH=4,
在Rt△AHC中,AC==2,
∵DE垂直平分AC,
∴CD=AC=,
∵ED⊥AC,
∴在Rt△EDC中,tanC==,
∴DE=.
13.(2018?沙湾区模拟)阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
【分析】(1)解直角三角形求出cosA,利用结论中的公式计算即可;
(2)利用图2,根据cos2A=cos∠CED=,计算即可;
【解答】解:(1)如图3中,在Rt△ABC中,∵AB=3,BC=1,∠C=90°,
∴AC==2,
∴sinA==,cosA=,
∴sinA=2cosA?sinA=
(2)如图2中,cos2A=cos∠CED===2AC?cosA﹣1=2(cosA)2﹣1.
14.(2018?大庆模拟)对于钝角α,定义它的三角函数值如下:sinα=sin(180°﹣α),cos=﹣cos(180°﹣α).
(1)求sin120°,cos150°的值;
(2)若一个直角三角形的三个内角比是1:1:4,A,B设这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
【分析】(1)仿照已知定义将各式变形,利用特殊角的三角函数值求出值即可;
(2)根据内角之比,利用内角和为180°求出各自的度数,根据sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求出m的值,进而确定出∠A和∠B的度数.
【解答】解:(1)由题意得:sin120°=sin(180°﹣120°)=sin60°=,cos150°=cos(180°﹣30°)=﹣cos30°=﹣;
(2)∵一个直角三角形的三个内角比是1:1:4,
∴三个内角分别为30°,30°,120°,
①当∠A=30°,∠B=120°时,方程的两根为,﹣,
把代入方程得:1﹣m﹣1=0,解得:m=0,
经检验﹣是4x2﹣1=0的根,故m=0;
②当∠A=120°,∠B=30°时,方程的两根为,,不符合题意;
③∠A=30°,∠B=30°时,方程两根为,,
把代入得:1﹣m﹣1=0,解得:m=0,
经检验不是方程4x2﹣1=0的根,不符合题意,
则m=0,∠A=30°,∠B=120°.
