2018年高中数学北师大版必修2课件:第二章解析几何初步2-2-2圆的一般方程课件(19张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第二章解析几何初步2-2-2圆的一般方程课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 660.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-10 00:00:00 | ||
图片预览






文档简介
课件19张PPT。圆的一般方程复习导入 1.圆心为 C(a,b),半径为 r (r>0) 的圆的
标准方程是什么?(x-a)2+(y-b)2=r2 3.方程x2+y2-2 x-4 y+1=0表示的图形是圆吗?
是不是不是圆(x-1)2+(y-2)2=4 x2 +y 2+Dx+Ey+F=0
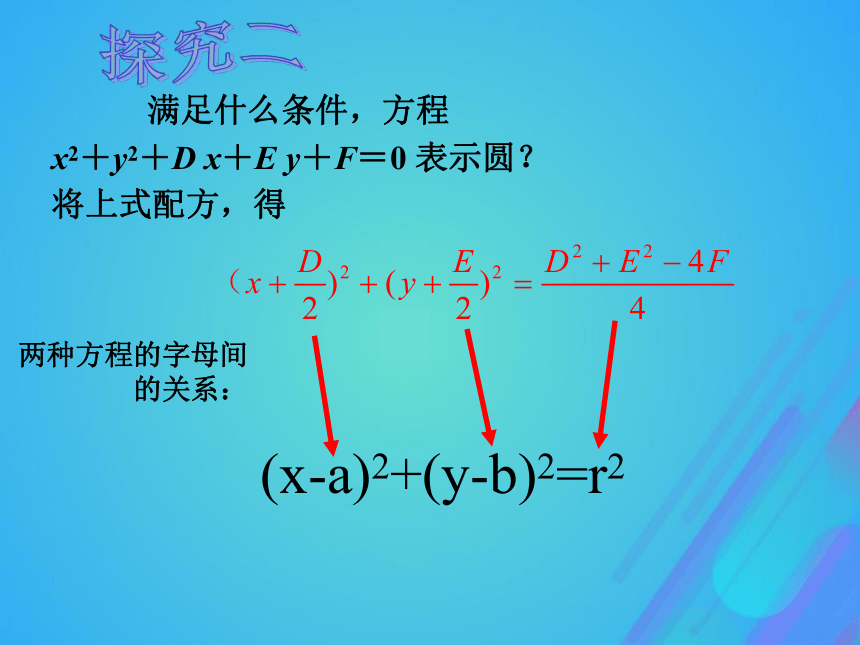
由于a, b, r均为常数结论:任何一个圆方程可以写成下面形式探究一问:是不是任何一个形如以上方程所表示的曲线,都是圆呢?探究二 满足什么条件,方程
x2+y2+D x+E y+F=0 表示圆?
将上式配方,得两种方程的字母间的关系:(x-a)2+(y-b)2=r2(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形新课探究,总结规律方程x2+y2+Dx+Ey+F=0表示圆的条件: 当 D2+E2-4 F>0时,方程
x2 +y2 +D x+E y+F=0
叫做圆的一般方程.圆的一般方程的定义:新授练一练:(2)已知方程x2 + y2-2 x-2y+m=0表示圆,则m的取值范围为_________.(1)已知圆的方程为x2 + y2-4 x-6 y+12=0,则其圆心坐标为_________,半径长为_____.(2,3) r =1其中圆心坐标 ,半径长m<2圆的标准方程与圆的一般方程各有什么特点? 圆的标准方程: (x-a)2+(y-b)2=r2. 指出了圆的圆心坐标与半径大小,几何特征明显. 圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)圆的方程是一种特殊的二元二次方程,代数特征明显.
1. A = C ≠ 0 2. B=03. D2+E2-4AF>0 二元二次方程表示圆的一般方程圆的一般方程与二元二次方程的关系 例1 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的半径长与圆心坐标.待定系数法典型例题归纳可得:
求圆的方程时,若已知条件与圆心和半径没有直接关系,则设一般方程;反之,则设标准方程. M2M1 将这个方程配方,得
(x-4)2+(y+3)2=25.
因此所求圆的圆心坐标是(4,-3),半径为 5. 解:设所求圆的方程为x2+y2+Dx+Ey+F=0,
其中 D,E,F 待定.由题意得解得:D=-8,E=6,F=0.于是所求圆的方程为x2+y2-8 x+6 y=0.解法一三元一次方程组解法二
解:设所求圆的方程为:因为O(0,0),M1(1,1), M2(4,2)都在圆上所求圆的方程为三元二次方程组 因此所求圆的圆心坐标是(4,-3),
半径为 5.注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:①若知道或涉及圆心和半径,我们一般采用
圆的标准方程较简单.②若已知三点求圆的方程,我们常常采用圆 的一般方程用待定系数法求解. [小结]:(特殊情况时,可借助图象求解更简单)3.解出a,b,r或D,E,F,代入标准方程或一般方程. 1.根据题意,选择标准方程或一般方程;2.根据条件列出关于a,b,r或D,E,F的方程组;“待定系数法”求圆的方程的一般步骤:设列解典型例题 例2 过点M(-1,1)且圆心与已知圆C:x2+y2-4x+6y-3=0相同的圆的方程解法一:将已知圆的方程化为标准方程
(x-2)2+(y+3)2=16,圆心C的坐标为(2,-3),半径为4,所求圆的方程为(x-2)2+(y+3)2=25.故所求圆的半径为
r=|CM| = =5
解法二:将已知圆C 化解成标准圆的方程:
(x - 2)2 + (y + 3)2 = 16
∴ 圆心 ( 2 , - 3 )
设所求圆的方程为 (x - 2)2 + (y + 3)2 = r2
∵点 M ( - 1 , 1) 在圆上,把 x = - 1 , y = 1
代入方程,得 r = 5
∴ 所求圆的方程为 (x - 2 )2 + ( y + 3 )2 = 25 2.平面直角坐标系中有A(0,0),B(8,0),C(0,-6),D(4,2)四点,这四点能否在同一个圆上?为什么? 1.已知圆的方程x2+y2+2x-4y-4=0,求其圆心坐标和半径长.随堂训练(-1,2),r=3. 由其中三点可确定圆的方程x2+y2-8x+6y=0,经验证第四个点也在此圆上.能这节课你收获了什么?想一想
运用了配方法、公式法、待定系数法解题; 2 .方法总结:归纳小结 圆的一般方程
x2+y2+D x+E y+F=0( D2+E2-4 F>0); 1.知识总结: YouThank欢迎批评指正
标准方程是什么?(x-a)2+(y-b)2=r2 3.方程x2+y2-2 x-4 y+1=0表示的图形是圆吗?
是不是不是圆(x-1)2+(y-2)2=4 x2 +y 2+Dx+Ey+F=0
由于a, b, r均为常数结论:任何一个圆方程可以写成下面形式探究一问:是不是任何一个形如以上方程所表示的曲线,都是圆呢?探究二 满足什么条件,方程
x2+y2+D x+E y+F=0 表示圆?
将上式配方,得两种方程的字母间的关系:(x-a)2+(y-b)2=r2(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形新课探究,总结规律方程x2+y2+Dx+Ey+F=0表示圆的条件: 当 D2+E2-4 F>0时,方程
x2 +y2 +D x+E y+F=0
叫做圆的一般方程.圆的一般方程的定义:新授练一练:(2)已知方程x2 + y2-2 x-2y+m=0表示圆,则m的取值范围为_________.(1)已知圆的方程为x2 + y2-4 x-6 y+12=0,则其圆心坐标为_________,半径长为_____.(2,3) r =1其中圆心坐标 ,半径长m<2圆的标准方程与圆的一般方程各有什么特点? 圆的标准方程: (x-a)2+(y-b)2=r2. 指出了圆的圆心坐标与半径大小,几何特征明显. 圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)圆的方程是一种特殊的二元二次方程,代数特征明显.
1. A = C ≠ 0 2. B=03. D2+E2-4AF>0 二元二次方程表示圆的一般方程圆的一般方程与二元二次方程的关系 例1 求过三点O(0,0),M1(1,1),M2(4,2)的圆的方程,并求出这个圆的半径长与圆心坐标.待定系数法典型例题归纳可得:
求圆的方程时,若已知条件与圆心和半径没有直接关系,则设一般方程;反之,则设标准方程. M2M1 将这个方程配方,得
(x-4)2+(y+3)2=25.
因此所求圆的圆心坐标是(4,-3),半径为 5. 解:设所求圆的方程为x2+y2+Dx+Ey+F=0,
其中 D,E,F 待定.由题意得解得:D=-8,E=6,F=0.于是所求圆的方程为x2+y2-8 x+6 y=0.解法一三元一次方程组解法二
解:设所求圆的方程为:因为O(0,0),M1(1,1), M2(4,2)都在圆上所求圆的方程为三元二次方程组 因此所求圆的圆心坐标是(4,-3),
半径为 5.注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:①若知道或涉及圆心和半径,我们一般采用
圆的标准方程较简单.②若已知三点求圆的方程,我们常常采用圆 的一般方程用待定系数法求解. [小结]:(特殊情况时,可借助图象求解更简单)3.解出a,b,r或D,E,F,代入标准方程或一般方程. 1.根据题意,选择标准方程或一般方程;2.根据条件列出关于a,b,r或D,E,F的方程组;“待定系数法”求圆的方程的一般步骤:设列解典型例题 例2 过点M(-1,1)且圆心与已知圆C:x2+y2-4x+6y-3=0相同的圆的方程解法一:将已知圆的方程化为标准方程
(x-2)2+(y+3)2=16,圆心C的坐标为(2,-3),半径为4,所求圆的方程为(x-2)2+(y+3)2=25.故所求圆的半径为
r=|CM| = =5
解法二:将已知圆C 化解成标准圆的方程:
(x - 2)2 + (y + 3)2 = 16
∴ 圆心 ( 2 , - 3 )
设所求圆的方程为 (x - 2)2 + (y + 3)2 = r2
∵点 M ( - 1 , 1) 在圆上,把 x = - 1 , y = 1
代入方程,得 r = 5
∴ 所求圆的方程为 (x - 2 )2 + ( y + 3 )2 = 25 2.平面直角坐标系中有A(0,0),B(8,0),C(0,-6),D(4,2)四点,这四点能否在同一个圆上?为什么? 1.已知圆的方程x2+y2+2x-4y-4=0,求其圆心坐标和半径长.随堂训练(-1,2),r=3. 由其中三点可确定圆的方程x2+y2-8x+6y=0,经验证第四个点也在此圆上.能这节课你收获了什么?想一想
运用了配方法、公式法、待定系数法解题; 2 .方法总结:归纳小结 圆的一般方程
x2+y2+D x+E y+F=0( D2+E2-4 F>0); 1.知识总结: YouThank欢迎批评指正
