2018年高中数学北师大版必修2课件:第二章解析几何初步2-3-1空间直角坐标系的建立课件(19张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第二章解析几何初步2-3-1空间直角坐标系的建立课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 374.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-10 20:44:24 | ||
图片预览




文档简介
课件19张PPT。§3 空间直角坐标系思考一: 在空间,我们是否可以建立一个坐标系,
使空间中的任意一点都可用对应的有序实数
组表示出来呢?猜想:空间中的点可用有序
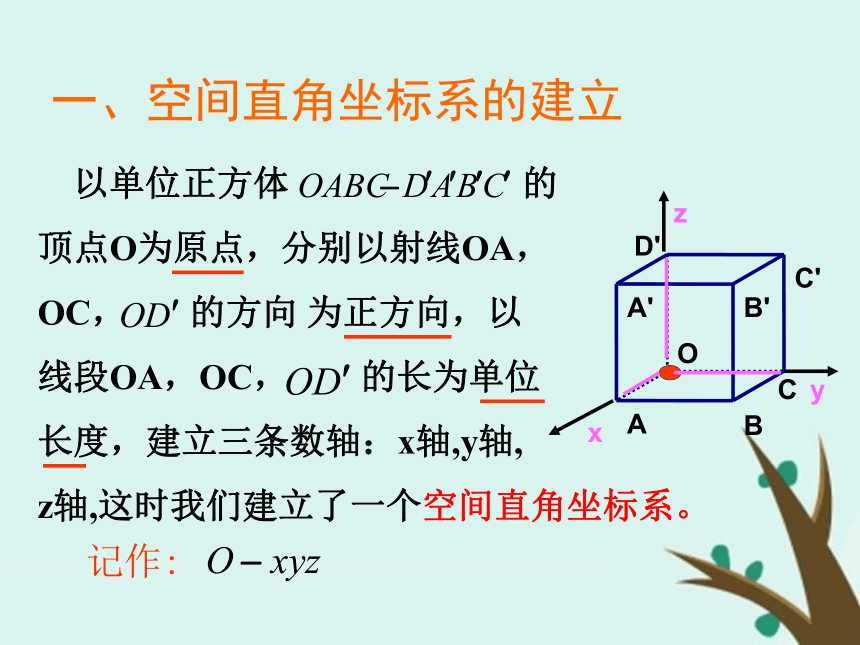
实数组(x,y,z)表示? 一、空间直角坐标系的建立1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)作图:∠xOy=135°∠yOz=90° 通过每两个坐标轴的
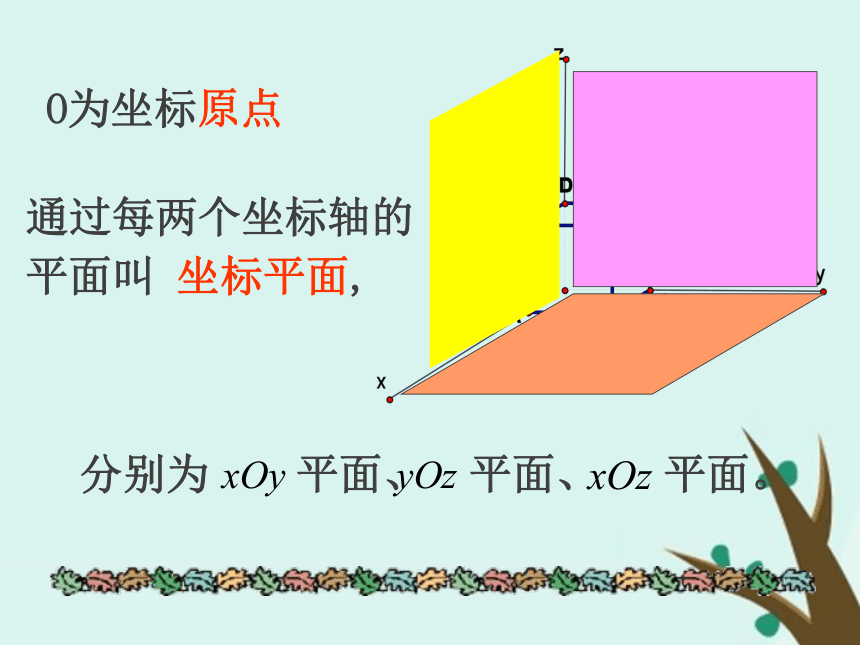
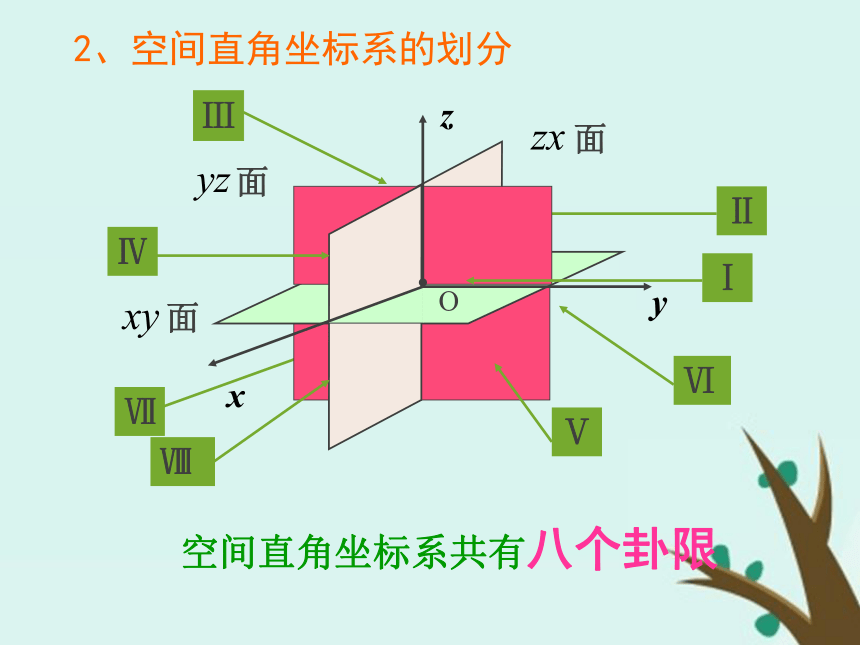
平面叫 坐标平面,O为坐标原点空间直角坐标系共有八个卦限2、空间直角坐标系的划分思考二: 空间直角坐标系中任意一点的位置如何表示?
??P0xyz P点坐标为
(x,y,z)P13、空间中点的坐标MN有序实数组(x,y,z)就叫做P的空间直角坐标,简称为坐标,记作P(x,y,z)。
小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标例1:如图D’ (0,0,2)C (0,4,0)A’ (3,0,2)B’ (3,4,2)练习:???ABC?DEF??1、在空间直角坐标系中描出下列各点,并说明这些点的位置
A(0,1,1) B(0,0,2) C(0,2,0)
D(1,0,3) E(2,2,0) F(1,0,0)(+,+,+)5、点P在各卦限中x、y、z坐标的符号(-,+,+)(-,-,+)(+,-,+)(+,+,-)(-,+,-)(-,-,-)(+,-,-)?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C练习:在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);M(x,y,z)N(x,-y,-z)思考:
设点M的坐标为(x,y,z),那么点M关于x轴对称的点的坐标分别是什么? 点M(x,y,z)是空间直角坐标系Oxyz中的一点,写出
满足下列条件的点的坐标.(1)与点M关于x轴对称的点(2)与点M关于y轴对称的点(3)与点M关于z轴对称的点(4)与点M关于原点对称的点(5)与点M关于xOy平面对称的点(6)与点M关于xOz平面对称的点(7)与点M关于yOz平面对称的点(x,-y,-z)(-x,y,-z)(-x,-y,z)(-x,-y,-z)(x,y,-z)(x,-y,z)(-x,y,z)练习:结论1:在空间直角坐标系Oxyz中,任意一点M(x,y,z)与原点的距离空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),
P2(x2,y2,z2)在xOy平面上的射影
分别为M、N.思考:点M、N之间的距离如何?思考:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?1.若在空间直角坐标系Oxyz中点P的坐标是(x,y,z),则P到坐标原点O的距离OP=__________.
2.在空间直角坐标系Oxyz中,设点P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,则P1与P2之间的距离P1P2=____________________.
3.在空间直角坐标系Oxyz中,点P(x0,y0,z0)到平面xOy的距离为_______,到x轴的距离为__________.|z0|
使空间中的任意一点都可用对应的有序实数
组表示出来呢?猜想:空间中的点可用有序
实数组(x,y,z)表示? 一、空间直角坐标系的建立1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)作图:∠xOy=135°∠yOz=90° 通过每两个坐标轴的
平面叫 坐标平面,O为坐标原点空间直角坐标系共有八个卦限2、空间直角坐标系的划分思考二: 空间直角坐标系中任意一点的位置如何表示?
??P0xyz P点坐标为
(x,y,z)P13、空间中点的坐标MN有序实数组(x,y,z)就叫做P的空间直角坐标,简称为坐标,记作P(x,y,z)。
小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标例1:如图D’ (0,0,2)C (0,4,0)A’ (3,0,2)B’ (3,4,2)练习:???ABC?DEF??1、在空间直角坐标系中描出下列各点,并说明这些点的位置
A(0,1,1) B(0,0,2) C(0,2,0)
D(1,0,3) E(2,2,0) F(1,0,0)(+,+,+)5、点P在各卦限中x、y、z坐标的符号(-,+,+)(-,-,+)(+,-,+)(+,+,-)(-,+,-)(-,-,-)(+,-,-)?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C练习:在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);M(x,y,z)N(x,-y,-z)思考:
设点M的坐标为(x,y,z),那么点M关于x轴对称的点的坐标分别是什么? 点M(x,y,z)是空间直角坐标系Oxyz中的一点,写出
满足下列条件的点的坐标.(1)与点M关于x轴对称的点(2)与点M关于y轴对称的点(3)与点M关于z轴对称的点(4)与点M关于原点对称的点(5)与点M关于xOy平面对称的点(6)与点M关于xOz平面对称的点(7)与点M关于yOz平面对称的点(x,-y,-z)(-x,y,-z)(-x,-y,z)(-x,-y,-z)(x,y,-z)(x,-y,z)(-x,y,z)练习:结论1:在空间直角坐标系Oxyz中,任意一点M(x,y,z)与原点的距离空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),
P2(x2,y2,z2)在xOy平面上的射影
分别为M、N.思考:点M、N之间的距离如何?思考:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?1.若在空间直角坐标系Oxyz中点P的坐标是(x,y,z),则P到坐标原点O的距离OP=__________.
2.在空间直角坐标系Oxyz中,设点P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,则P1与P2之间的距离P1P2=____________________.
3.在空间直角坐标系Oxyz中,点P(x0,y0,z0)到平面xOy的距离为_______,到x轴的距离为__________.|z0|
