2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(18张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 862.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-10 20:53:52 | ||
图片预览




文档简介
课件18张PPT。平行关系的性质问题提出1.直线与平面平行和平面与平面平行的判定定理是什么?2.直线与平面平行的判定定理和平面与平面平行的判定定理解决了直线与平面平行和平面与平面平行的条件问题,反之,在直线与平面平行和平面与平面平行的条件下,可以得到什么结论呢?定理 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
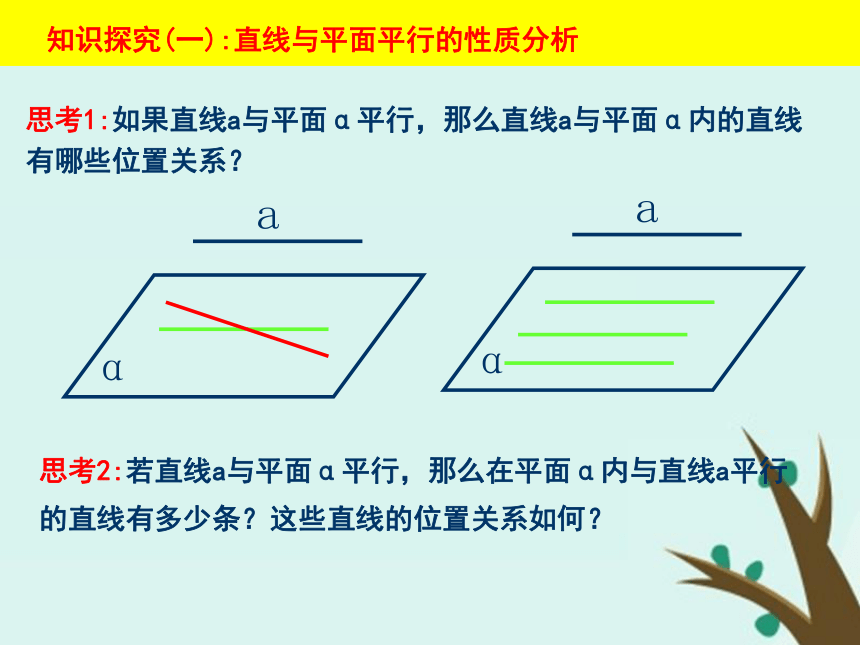
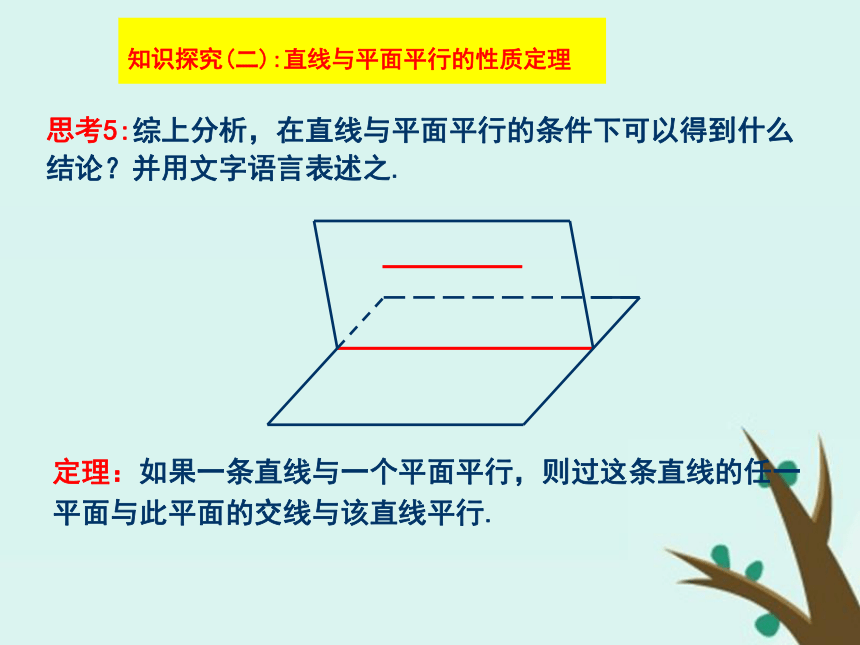
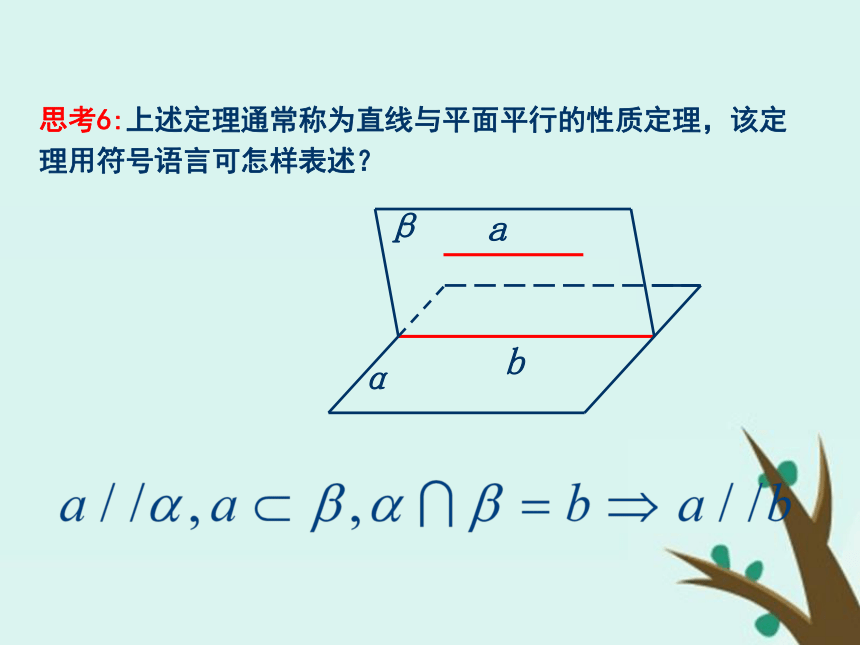
知识探究(一):直线与平面平行的性质分析 思考1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?思考2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?思考3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?思考4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?知识探究(二):直线与平面平行的性质定理 思考5:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 思考6:上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述?思考7:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 例1 如图所示的一块木料中,棱BC平行于面A′C′.
(1)要经过面A′C′ 内一点P和棱BC将木料锯开,应怎样 画线?
(2)所画的线与平面AC是什么位置关系? 解:(1)在平面A’B’C’D’内过点P作直线EF∥B’C’,分别交A’B’,C’D’于E,F,连结BE,CF,(2)EF∥平面ACEF例2. 如图,已知直线a,b和平面α ,a∥b,a∥α ,a,b都在平面α外 .求证:b∥α . 证明:过直线a作平面β交平面α于直线c,∵a∥α∴a∥c,又a∥b,∴b∥c,而b α,c α ∴b∥α 知识探究(三):平面与平面平行的性质分析 思考8:若 ,则直线l与平面β的位置关系如何? 思考2:若 ,直线l与平面α平行,那么直线l与平面β的位置关系如何?思考10:若 ,平面α与平面γ相交,则平面β与平面γ的位置关系如何? 思考9:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?思考11:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?思考12:由思考5反映出来的性质就是一个定理,分别用文字语言和符号语言可以怎样表述?定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.思考13:上述定理通常称为平面与平面平行的性质定理,该定理在实际应用中有何功能作用? 判定两直线平行的依据例3.如下图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,AC∩β=B,DF∩β=E.
求证:
同理,
∴证明:连结BM、EM、BE.∵β∥γ,平面ACF分别交β、
γ于BM、CF,∴BM∥CF.∴1.直线与平面平行和平面与平面平行的性质:2.数学思想方法:转化的思想知识小结谢谢大家!
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
知识探究(一):直线与平面平行的性质分析 思考1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?思考2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?思考3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?思考4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?知识探究(二):直线与平面平行的性质定理 思考5:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 思考6:上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述?思考7:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 例1 如图所示的一块木料中,棱BC平行于面A′C′.
(1)要经过面A′C′ 内一点P和棱BC将木料锯开,应怎样 画线?
(2)所画的线与平面AC是什么位置关系? 解:(1)在平面A’B’C’D’内过点P作直线EF∥B’C’,分别交A’B’,C’D’于E,F,连结BE,CF,(2)EF∥平面ACEF例2. 如图,已知直线a,b和平面α ,a∥b,a∥α ,a,b都在平面α外 .求证:b∥α . 证明:过直线a作平面β交平面α于直线c,∵a∥α∴a∥c,又a∥b,∴b∥c,而b α,c α ∴b∥α 知识探究(三):平面与平面平行的性质分析 思考8:若 ,则直线l与平面β的位置关系如何? 思考2:若 ,直线l与平面α平行,那么直线l与平面β的位置关系如何?思考10:若 ,平面α与平面γ相交,则平面β与平面γ的位置关系如何? 思考9:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?思考11:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?思考12:由思考5反映出来的性质就是一个定理,分别用文字语言和符号语言可以怎样表述?定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.思考13:上述定理通常称为平面与平面平行的性质定理,该定理在实际应用中有何功能作用? 判定两直线平行的依据例3.如下图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,AC∩β=B,DF∩β=E.
求证:
同理,
∴证明:连结BM、EM、BE.∵β∥γ,平面ACF分别交β、
γ于BM、CF,∴BM∥CF.∴1.直线与平面平行和平面与平面平行的性质:2.数学思想方法:转化的思想知识小结谢谢大家!
