第4章 图形的初步认识单元考试题(有答案)
文档属性
| 名称 | 第4章 图形的初步认识单元考试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-10 13:16:09 | ||
图片预览



文档简介
华师大版数学七年级上册第4章图形的初步认识单元考试题
总分:100分,时间:90分钟;
姓名: ;成绩: ;
选择题(3分×10=30分)
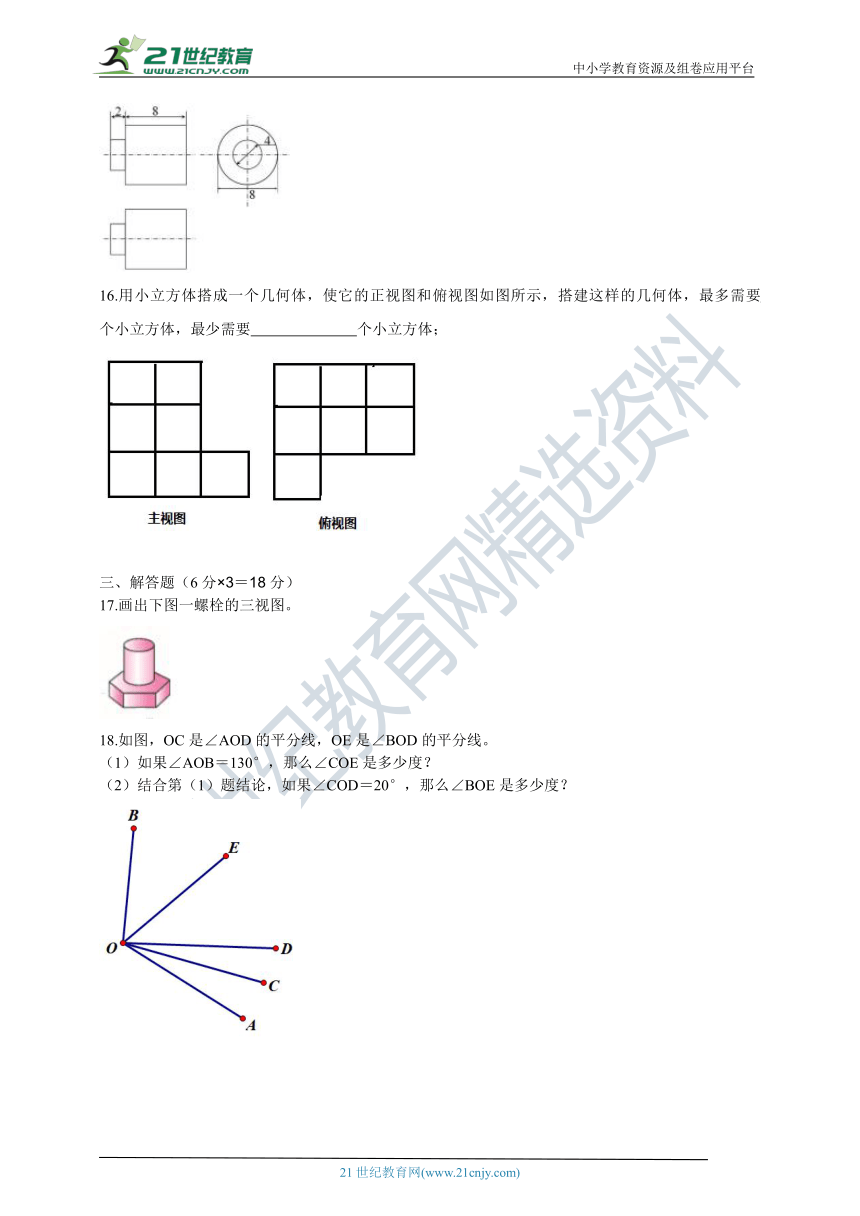
1.下列图形中,是三棱锥的是( )
如图是由5个完全相同是正方体组成的立体图形,它的主视图是( )
3.钟表上,8点30分时,时针与分针的夹角是 ( )
A.90° B.85° C.75° D.60°
4.用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,另一个是 30°,60°,90°)可以画出大于0°且小于180°的不同度数的角共有( )
A.8种 B.9种 C.10种 D.11种
两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有( )个交点.
A.45 B.42 C.40 D.36
6.点A、B、C都在同一条直线上,AB=8cm,BC=10cm,则线段AC长为( )
A.18cm或2cm B、18cm C.2cm D、8cm或10cm
7.下列四个生活中产生的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵的位置,就能确定同一行树所在的直线;③从A地到B架设电线,总是尽可能沿着线段AB方向架设;④把弯曲的公路改直,就能缩短路程。
其中可用公理“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②③ D.③④
8.如图,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )
∠AOC=∠BOD B.∠COD=∠AOB C.∠AOC=∠AOD D.∠BOD=∠BOC
9.下列说法正确的是( )
A、一个锐角的余角比这个角的补角小90°;
B、如果一个角有补角,那么这个角必是钝角;
C、若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为了补角;
D、如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角。
10.点B在线段AC上,以下四个等式①AB=BC;②BC=AC;③AC=2AB;④BC=AB.其中能表示B是AC的中点的有( )
A.1个 B、2个 C、3个 D.4个
二、填空题(3分×6=18分)
11.下面是一个正方体的展开图,图中已标出三个面在正方体中的位置,E表示前面,F表示右面,D表示上面,则A表示 ,B表示 ,C表示 ;
12..如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点。
如果MN=12cm,则AB= cm;
13.已知,则∠α的余角是 ;∠α的补角是 ;
14.在直线a上若有2个点,则有1条线段;若有3个点,则有3条线段;若有4个点,则有6条线段;若有n个点,则有 条线段;
15.如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为 ;
16.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多需要 个小立方体,最少需要 个小立方体;
解答题(6分×3=18分)
画出下图一螺栓的三视图。
18.如图,OC是∠AOD的平分线,OE是∠BOD的平分线。
(1)如果∠AOB=130°,那么∠COE是多少度?
(2)结合第(1)题结论,如果∠COD=20°,那么∠BOE是多少度?
19.如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,求AD的长。
解答题(8+8+8+10=34)
20.如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.
21.如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
(1)若∠COD=30°,求∠BOE的度数;
(2)若∠BOE=85°,求∠COD的度数.(提示:设∠COD=x°)
22.回答问题:
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=CB,点D是直线AB上满足BD=AC.请画出示意图,求出线段CD的长.
23.将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
华师大版数学七年级上册第4章图形的初步认识单元考试题答案
选择题
BBCDA DDBAB
填空题
后面,下面,左面; 12.24; 13.,;
14.; 15.136; 16.16,11;
解答题
(1)65°,(2)45°;
19.4.5cm;
解答题
(1)120°,猜想∠BOC+∠AOD=180°;(2)∠BOC=(2x﹣y)°.
(1)75°;(2)∠COD=40°.
(1)45°,(2)线段CD的长是6cm或10cm.
23.(1)2.25,45;(3)①5或10,②∠NOC﹣∠AOM=15°.
总分:100分,时间:90分钟;
姓名: ;成绩: ;
选择题(3分×10=30分)
1.下列图形中,是三棱锥的是( )
如图是由5个完全相同是正方体组成的立体图形,它的主视图是( )
3.钟表上,8点30分时,时针与分针的夹角是 ( )
A.90° B.85° C.75° D.60°
4.用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,另一个是 30°,60°,90°)可以画出大于0°且小于180°的不同度数的角共有( )
A.8种 B.9种 C.10种 D.11种
两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有( )个交点.
A.45 B.42 C.40 D.36
6.点A、B、C都在同一条直线上,AB=8cm,BC=10cm,则线段AC长为( )
A.18cm或2cm B、18cm C.2cm D、8cm或10cm
7.下列四个生活中产生的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵的位置,就能确定同一行树所在的直线;③从A地到B架设电线,总是尽可能沿着线段AB方向架设;④把弯曲的公路改直,就能缩短路程。
其中可用公理“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②③ D.③④
8.如图,OC平分∠AOD,OD平分∠BOC,下列等式不成立的是( )
∠AOC=∠BOD B.∠COD=∠AOB C.∠AOC=∠AOD D.∠BOD=∠BOC
9.下列说法正确的是( )
A、一个锐角的余角比这个角的补角小90°;
B、如果一个角有补角,那么这个角必是钝角;
C、若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为了补角;
D、如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角。
10.点B在线段AC上,以下四个等式①AB=BC;②BC=AC;③AC=2AB;④BC=AB.其中能表示B是AC的中点的有( )
A.1个 B、2个 C、3个 D.4个
二、填空题(3分×6=18分)
11.下面是一个正方体的展开图,图中已标出三个面在正方体中的位置,E表示前面,F表示右面,D表示上面,则A表示 ,B表示 ,C表示 ;
12..如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点。
如果MN=12cm,则AB= cm;
13.已知,则∠α的余角是 ;∠α的补角是 ;
14.在直线a上若有2个点,则有1条线段;若有3个点,则有3条线段;若有4个点,则有6条线段;若有n个点,则有 条线段;
15.如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为 ;
16.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多需要 个小立方体,最少需要 个小立方体;
解答题(6分×3=18分)
画出下图一螺栓的三视图。
18.如图,OC是∠AOD的平分线,OE是∠BOD的平分线。
(1)如果∠AOB=130°,那么∠COE是多少度?
(2)结合第(1)题结论,如果∠COD=20°,那么∠BOE是多少度?
19.如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,求AD的长。
解答题(8+8+8+10=34)
20.如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.
21.如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
(1)若∠COD=30°,求∠BOE的度数;
(2)若∠BOE=85°,求∠COD的度数.(提示:设∠COD=x°)
22.回答问题:
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=CB,点D是直线AB上满足BD=AC.请画出示意图,求出线段CD的长.
23.将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
华师大版数学七年级上册第4章图形的初步认识单元考试题答案
选择题
BBCDA DDBAB
填空题
后面,下面,左面; 12.24; 13.,;
14.; 15.136; 16.16,11;
解答题
(1)65°,(2)45°;
19.4.5cm;
解答题
(1)120°,猜想∠BOC+∠AOD=180°;(2)∠BOC=(2x﹣y)°.
(1)75°;(2)∠COD=40°.
(1)45°,(2)线段CD的长是6cm或10cm.
23.(1)2.25,45;(3)①5或10,②∠NOC﹣∠AOM=15°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
