第五章 平行四边形单元测试题(含答案)
图片预览


文档简介
第五章单元测试题
(60分钟 100分)
一、精心选一选(每题3分,共24分)
1.八边形的外角和是( )
A.180° B.360° C.1080o D.1440°
2.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD CAB=CD D.AC⊥BD
3.如图,在Rt△ABC中,∠A=30°,DE=1,点D,E分别是直角边BC,AC的中点,则AC的长为( )
A.1 B.2 C. D.1+
4.如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,AB=EF=2,若△CEF的面积为5,则
△ABD的面积为( )
A.2 B.4 C.5 D.10
5.四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B AB=DC,AD=BC
C AO=CO, BO= DO D.AB∥DC,AD=BC
6.(2018 株洲)已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,E是线段BC的中点,则以下说法错误的是( )
A.OE=DC B OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
7.在 ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在对角线BD上,图中面积相等的平行四边形有( )
A.0对 B.1对 C.2对 D.3对
8.在如图所示的四边形ABCD中,∠ABC=∠ADC,∠BAD=∠BCD,AC,BD相交于点O.小雨同学用大头针把一根平放在四边形上的细木条固定在点O处,拨动细木条,使它随意停留在任意位置(设细木条与边分别相交于点E,F),小雨观察几次拨动的结果发现:
①OE=OF;②AE=CF:③DE=BF;④△AOE≌△COF;⑤△DOE≌△BOF.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
二、细心填一填(每题3分,共24分)
9.如图,在同一平面内,将边长相等的正三角形与正五边形的一边重合,则∠1=_____________。
10.(2018 江西)如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为________________。
11.如图,在 ABCD中,点E,F分别在边BC,AD上,可添加条件:_____________________,使四边形AECF是平行四边形(只填一个即可)。
12.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是_____________。
13.如图,在等腰Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为_______________。
14.在平面直角坐标系中,A(1,0),B(0,2),C(-4,2),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为________________。
15.如图,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为___________。
16.如图,在 ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折90°到其原来所在的另一平面内,若点B的落点记为B',则DB'的长为_______________。
三、用心解一解(共52分)
17.(6分)在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数。
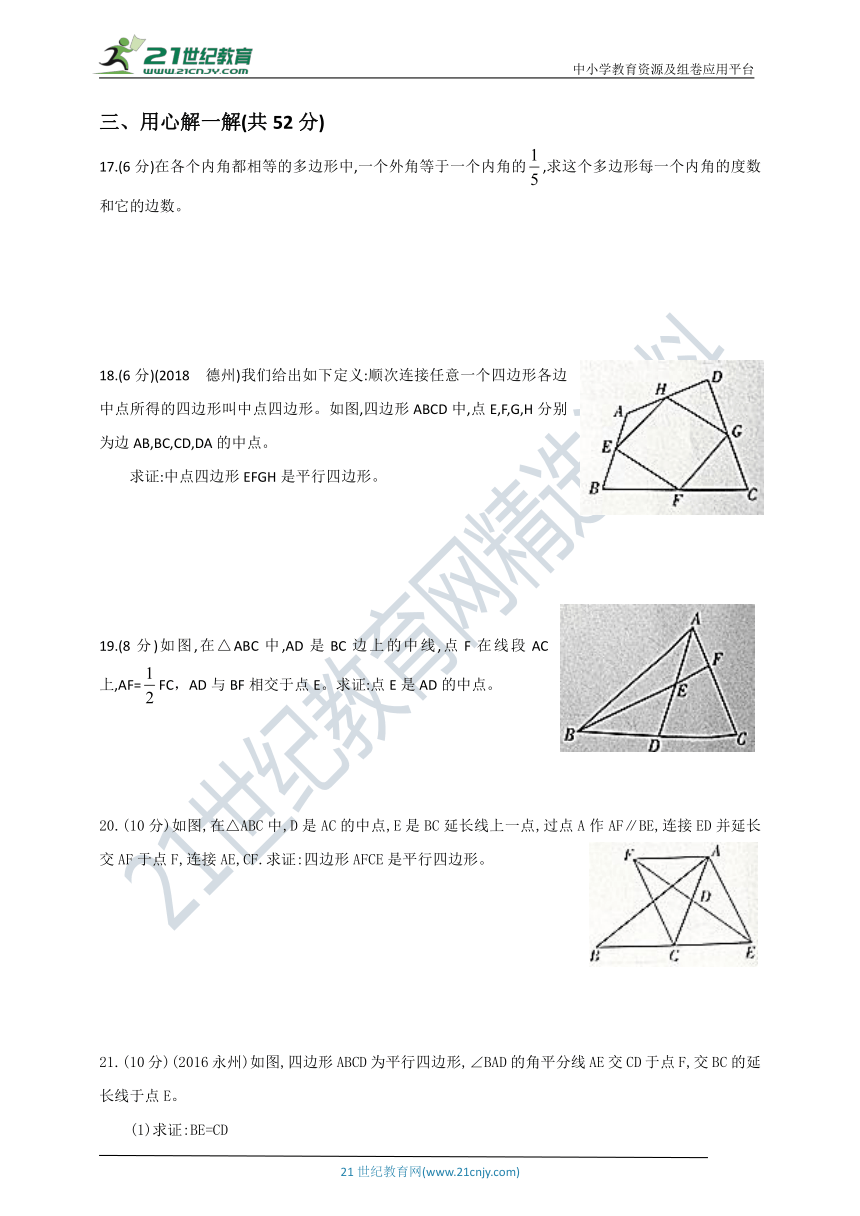
18.(6分)(2018 德州)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形。如图,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点。
求证:中点四边形EFGH是平行四边形。
19.(8分)如图,在△ABC中,AD是BC边上的中线,点F在线段AC上,AF=FC,AD与BF相交于点E。求证:点E是AD的中点。
20.(10分)如图,在△ABC中,D是AC的中点,E是BC延长线上一点,过点A作AF∥BE,连接ED并延长交AF于点F,连接AE,CF.求证:四边形AFCE是平行四边形。
21.(10分)(2016永州)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E。
(1)求证:BE=CD
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积。
22.(12分)如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G。
求证:(1)四边形AECF是平行四边形;
(2)EF与GH互相平分。
参考答案及解析
1.B 2.D 3.C 4.C 5.D 6.D 7.D 8.A 9.48 10.50°
11.答案不唯一,如BE=DF 12.35 13.8 14.(-3,0)或(5,0)或(-5,4)
15. 16.3
17.解:设这个多边形的每个内角为x0,那么180-x=x,解得x=150,那么边数为360÷(180-150)=12,故这个多边形的每一个内角的度数为150度,它的边数为12。
18.证明:如图,连接BD。
∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD,
∵点F,G分别为边BC,CD的中点, ∴FG∥BD,FG=BD,
∴EH∥FG,EH=GF,
∴中点四边形EFGH是平行四边形。
19.证明:取线段CF得中点M,连接DM ∵AF=FC,∴AF=FM=CM,
∵AD是BC边上的中线,∴BD=CD,∴DM是△BFC的中位线,∴DM∥BF,
∵AF=FM,∴AE=DE,即点E是AD的中点。
20.证明:∵D是AC的中点,∴AD=CD,∵AF∥BE,∴∠DAF=∠DCE.在△ADF和△CDE中,
∠DAF=∠DCE,AD=CD,∠ADF=∠CDE,∴△ADF≌△CDE,∴AF=CE,∴四边形AFCE是平行四边形。
21.(1)证明:∵四边形ABCD是平行四边形, AD∥BC,AB∥CD,AB=CD,
∴∠ABC+∠DCB=180°,∠AEB=∠DAE,
∵AE是∠BAD的角平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB, ∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,∴AE=AB=4, ∵BF⊥AE,∴AF=EF=2,
∴BF===,
∵AD∥BC,∴∠D=∠ECF,∠DAF=∠E,在△ADF和△ECF中,
∠D=∠ECF,∠DAF=∠E, AF-EF, ∴△ADF≌△ECF(AAS),
∴S△ADF=S△ECF,∴ SABCD=S△ABE=AE·BF=×4×=4。
22.证明:(1)∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∵AE=CF,
∴四边形AECF是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,∴AF∥CE, ∵AE=CF,AB∥CD,AB=CD, ∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,∴BF∥DE
∴四边形EGFH是平行四边形,∴EF与GH互相平分。
(60分钟 100分)
一、精心选一选(每题3分,共24分)
1.八边形的外角和是( )
A.180° B.360° C.1080o D.1440°
2.如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD CAB=CD D.AC⊥BD
3.如图,在Rt△ABC中,∠A=30°,DE=1,点D,E分别是直角边BC,AC的中点,则AC的长为( )
A.1 B.2 C. D.1+
4.如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,AB=EF=2,若△CEF的面积为5,则
△ABD的面积为( )
A.2 B.4 C.5 D.10
5.四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B AB=DC,AD=BC
C AO=CO, BO= DO D.AB∥DC,AD=BC
6.(2018 株洲)已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,E是线段BC的中点,则以下说法错误的是( )
A.OE=DC B OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
7.在 ABCD中,EF∥BC,GH∥AB,EF,GH的交点P在对角线BD上,图中面积相等的平行四边形有( )
A.0对 B.1对 C.2对 D.3对
8.在如图所示的四边形ABCD中,∠ABC=∠ADC,∠BAD=∠BCD,AC,BD相交于点O.小雨同学用大头针把一根平放在四边形上的细木条固定在点O处,拨动细木条,使它随意停留在任意位置(设细木条与边分别相交于点E,F),小雨观察几次拨动的结果发现:
①OE=OF;②AE=CF:③DE=BF;④△AOE≌△COF;⑤△DOE≌△BOF.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
二、细心填一填(每题3分,共24分)
9.如图,在同一平面内,将边长相等的正三角形与正五边形的一边重合,则∠1=_____________。
10.(2018 江西)如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为________________。
11.如图,在 ABCD中,点E,F分别在边BC,AD上,可添加条件:_____________________,使四边形AECF是平行四边形(只填一个即可)。
12.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是_____________。
13.如图,在等腰Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为_______________。
14.在平面直角坐标系中,A(1,0),B(0,2),C(-4,2),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为________________。
15.如图,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为___________。
16.如图,在 ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折90°到其原来所在的另一平面内,若点B的落点记为B',则DB'的长为_______________。
三、用心解一解(共52分)
17.(6分)在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数。
18.(6分)(2018 德州)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形。如图,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点。
求证:中点四边形EFGH是平行四边形。
19.(8分)如图,在△ABC中,AD是BC边上的中线,点F在线段AC上,AF=FC,AD与BF相交于点E。求证:点E是AD的中点。
20.(10分)如图,在△ABC中,D是AC的中点,E是BC延长线上一点,过点A作AF∥BE,连接ED并延长交AF于点F,连接AE,CF.求证:四边形AFCE是平行四边形。
21.(10分)(2016永州)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E。
(1)求证:BE=CD
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积。
22.(12分)如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G。
求证:(1)四边形AECF是平行四边形;
(2)EF与GH互相平分。
参考答案及解析
1.B 2.D 3.C 4.C 5.D 6.D 7.D 8.A 9.48 10.50°
11.答案不唯一,如BE=DF 12.35 13.8 14.(-3,0)或(5,0)或(-5,4)
15. 16.3
17.解:设这个多边形的每个内角为x0,那么180-x=x,解得x=150,那么边数为360÷(180-150)=12,故这个多边形的每一个内角的度数为150度,它的边数为12。
18.证明:如图,连接BD。
∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD,
∵点F,G分别为边BC,CD的中点, ∴FG∥BD,FG=BD,
∴EH∥FG,EH=GF,
∴中点四边形EFGH是平行四边形。
19.证明:取线段CF得中点M,连接DM ∵AF=FC,∴AF=FM=CM,
∵AD是BC边上的中线,∴BD=CD,∴DM是△BFC的中位线,∴DM∥BF,
∵AF=FM,∴AE=DE,即点E是AD的中点。
20.证明:∵D是AC的中点,∴AD=CD,∵AF∥BE,∴∠DAF=∠DCE.在△ADF和△CDE中,
∠DAF=∠DCE,AD=CD,∠ADF=∠CDE,∴△ADF≌△CDE,∴AF=CE,∴四边形AFCE是平行四边形。
21.(1)证明:∵四边形ABCD是平行四边形, AD∥BC,AB∥CD,AB=CD,
∴∠ABC+∠DCB=180°,∠AEB=∠DAE,
∵AE是∠BAD的角平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB, ∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,∴AE=AB=4, ∵BF⊥AE,∴AF=EF=2,
∴BF===,
∵AD∥BC,∴∠D=∠ECF,∠DAF=∠E,在△ADF和△ECF中,
∠D=∠ECF,∠DAF=∠E, AF-EF, ∴△ADF≌△ECF(AAS),
∴S△ADF=S△ECF,∴ SABCD=S△ABE=AE·BF=×4×=4。
22.证明:(1)∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∵AE=CF,
∴四边形AECF是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,∴AF∥CE, ∵AE=CF,AB∥CD,AB=CD, ∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,∴BF∥DE
∴四边形EGFH是平行四边形,∴EF与GH互相平分。
