含参数的二次函数最值问题(自制)
文档属性
| 名称 | 含参数的二次函数最值问题(自制) |

|
|
| 格式 | zip | ||
| 文件大小 | 781.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-12 00:00:00 | ||
图片预览






文档简介
含参数的二次函数最值问题
高中数学教师欧阳文丰
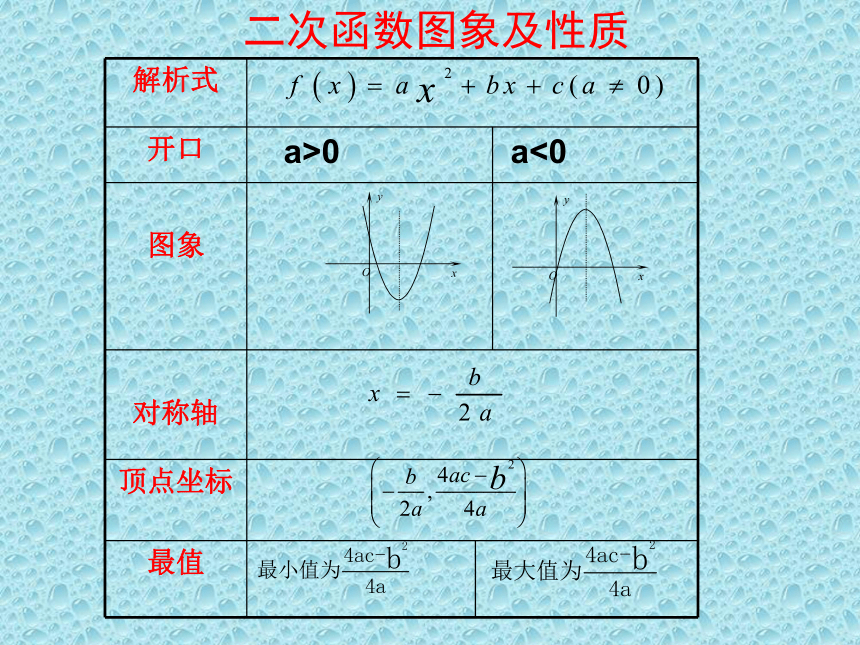
二次函数图象及性质
解析式
开口 a>0 a<0
图象
对称轴
顶点坐标
最值
求二次函数f(x)=ax2+bx+c在[m,n]上的最值或值域的一般方法是:
(2)当x0∈[m,n]时,f(m)、f(n)、f(x0)
中的较大者是最大值,较小者是最小值;
闭区间上二次函数的最值解题方法
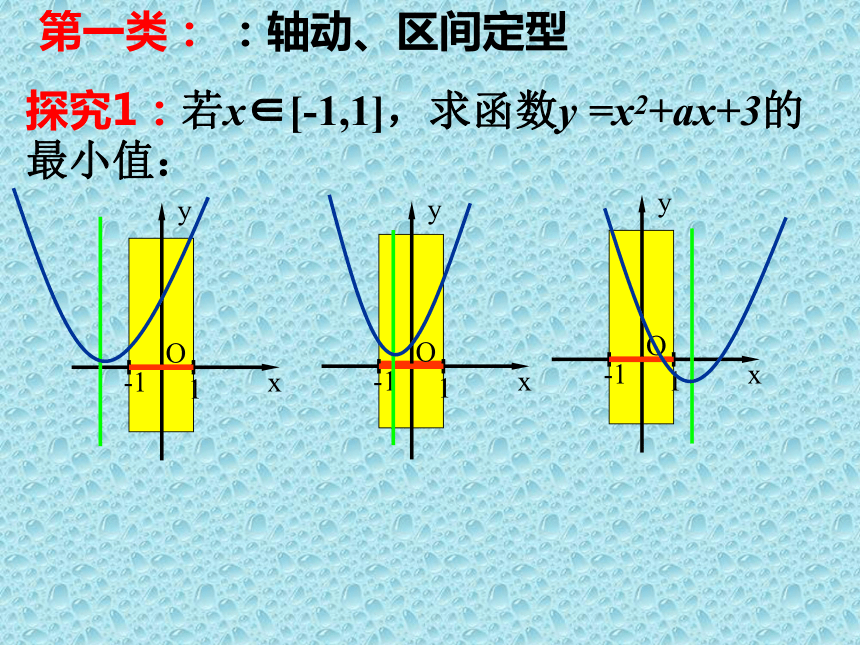
探究1:若x∈[-1,1],求函数y =x2+ax+3的最小值:
第一类: :轴动、区间定型
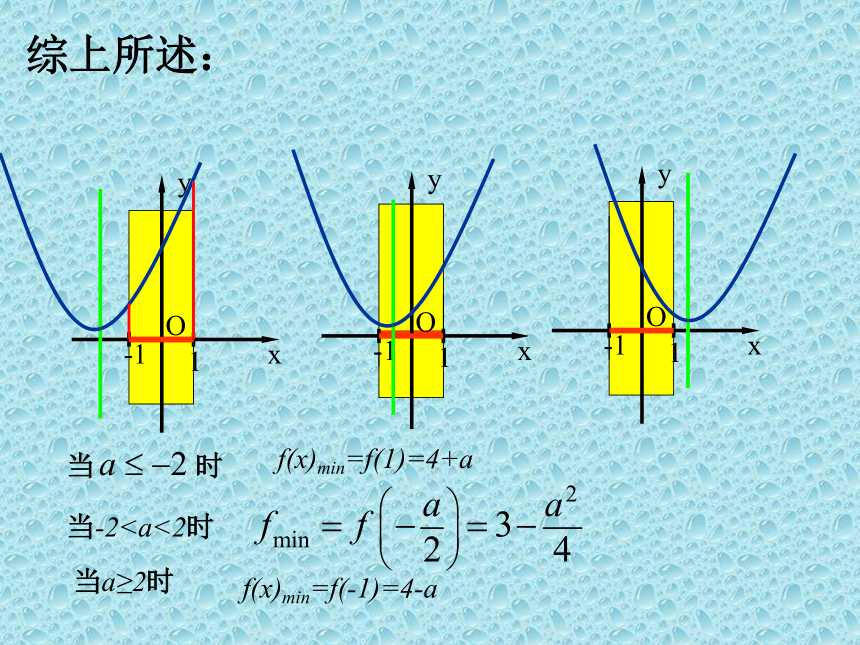
综上所述:
当 时
f(x)min=f(1)=4+a
当-2当a≥2时
f(x)min=f(-1)=4-a
评注:探究1属于“轴动区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
第一类: :轴动、区间定型
典型例题讲解
典型例题讲解
解:由题知,
函数f(x)的对称轴为x=a,开口向上
若 ,则函数f(x)的最小值为f(0)=—1
若 ,则函数f(x)的最小值为
若 ,则函数f(x)的最小值为f(2)=3—4a.
所以,
1、求二次函数f(x)=x2-2ax-1在区间[0,2]上的最小值?
变式练习一
变式练习一
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
解析:
因为函数 y=x2-2x-3=(x-1)2-4的对称
轴为 x=1 固定不变,要求函数的最值,即要看区间[k,k+2]与对称轴 x=1的位置,则从以下几个方面解决如图:
第二类: :轴定、区间动型
解:(1)当k+2≤1即k ≤-1时
f(x)min=f(k+2)
=(k+2)2-2(k+2)-3
=k2+2k-3
f(x)max=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
(2)当 k <1 < k+2 时 即-1 <k <1时
f(x)min=f(1)=- 4
①当f(k)>f(k+2)时,
即k2-2k-3 > k2+2k-3 即-1f(x)max=f(k)=k2-2k-3
②当f(k) ≤f(k+2)时,
即k2-2k-3 ≤ k2+2k-3 即0≤ k<1时
f(x)max=f(k+2)=(k+2)2-2(k+2)-3
=k2+2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
(3)当k ≥1时
f(x) max=f(k+2)=k2+2k-3
f(x) min=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
综上所述:
当k ≤-1时
当-1f(x)max=f(k)=k2-2k-3
当0≤ k<1时
f(x)max=f(k+2)=k2+2k-3
f(x)min=f(1)=- 4
f(x)min=f(1)=- 4
f(x)min=f(k+2)=k2+2k-3
f(x)max=f(k)=k2-2k-3
当k ≥1 时
f(x) max=f(k+2)=k2+2k-3
f(x) min=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
评注:探究2属于“轴定区间动”的问题,看作动区间沿x轴移动的过程中,函数最值的变化,即动区间在定轴的左、右两侧及包含定轴的变化,要注意开口方向及端点情况。
第二类: :轴定、区间动型
,
解:
的对称轴是
当
即
的最小值是
当
,即
当
当
时,
时
,或
在区间
上是减函数
的最小值是
时,
在区间
上是增函数
的最小值是
例3、已知函数f(x)= x2 –2x – 3.
x∈[ t,t+1 ],求函数f(x)的最小值;
典型例题讲解
典型例题讲解
变式练习二
解:
的对称轴是
当
,即
时,
的最大值是
当
,即
或
时;
当
时,
在区间
上是增函数
的最大值是
当
时,
在区间
上是减函数
的最大值是
变式练习二
本节课讨论了两类含参数的二次函数最值问题:
(1)轴动区间定 (2)轴定区间动
核心思想仍然是判断对称轴与区间的相对位置,从中体会到数形结合思想、分类讨论思想。
小结:
高中数学教师欧阳文丰
二次函数图象及性质
解析式
开口 a>0 a<0
图象
对称轴
顶点坐标
最值
求二次函数f(x)=ax2+bx+c在[m,n]上的最值或值域的一般方法是:
(2)当x0∈[m,n]时,f(m)、f(n)、f(x0)
中的较大者是最大值,较小者是最小值;
闭区间上二次函数的最值解题方法
探究1:若x∈[-1,1],求函数y =x2+ax+3的最小值:
第一类: :轴动、区间定型
综上所述:
当 时
f(x)min=f(1)=4+a
当-2
f(x)min=f(-1)=4-a
评注:探究1属于“轴动区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
第一类: :轴动、区间定型
典型例题讲解
典型例题讲解
解:由题知,
函数f(x)的对称轴为x=a,开口向上
若 ,则函数f(x)的最小值为f(0)=—1
若 ,则函数f(x)的最小值为
若 ,则函数f(x)的最小值为f(2)=3—4a.
所以,
1、求二次函数f(x)=x2-2ax-1在区间[0,2]上的最小值?
变式练习一
变式练习一
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
解析:
因为函数 y=x2-2x-3=(x-1)2-4的对称
轴为 x=1 固定不变,要求函数的最值,即要看区间[k,k+2]与对称轴 x=1的位置,则从以下几个方面解决如图:
第二类: :轴定、区间动型
解:(1)当k+2≤1即k ≤-1时
f(x)min=f(k+2)
=(k+2)2-2(k+2)-3
=k2+2k-3
f(x)max=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
(2)当 k <1 < k+2 时 即-1 <k <1时
f(x)min=f(1)=- 4
①当f(k)>f(k+2)时,
即k2-2k-3 > k2+2k-3 即-1
②当f(k) ≤f(k+2)时,
即k2-2k-3 ≤ k2+2k-3 即0≤ k<1时
f(x)max=f(k+2)=(k+2)2-2(k+2)-3
=k2+2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
(3)当k ≥1时
f(x) max=f(k+2)=k2+2k-3
f(x) min=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
综上所述:
当k ≤-1时
当-1
当0≤ k<1时
f(x)max=f(k+2)=k2+2k-3
f(x)min=f(1)=- 4
f(x)min=f(1)=- 4
f(x)min=f(k+2)=k2+2k-3
f(x)max=f(k)=k2-2k-3
当k ≥1 时
f(x) max=f(k+2)=k2+2k-3
f(x) min=f(k)=k2-2k-3
探究2:如何 求函数y=x2-2x-3,x∈[k,k+2]时的最值?
评注:探究2属于“轴定区间动”的问题,看作动区间沿x轴移动的过程中,函数最值的变化,即动区间在定轴的左、右两侧及包含定轴的变化,要注意开口方向及端点情况。
第二类: :轴定、区间动型
,
解:
的对称轴是
当
即
的最小值是
当
,即
当
当
时,
时
,或
在区间
上是减函数
的最小值是
时,
在区间
上是增函数
的最小值是
例3、已知函数f(x)= x2 –2x – 3.
x∈[ t,t+1 ],求函数f(x)的最小值;
典型例题讲解
典型例题讲解
变式练习二
解:
的对称轴是
当
,即
时,
的最大值是
当
,即
或
时;
当
时,
在区间
上是增函数
的最大值是
当
时,
在区间
上是减函数
的最大值是
变式练习二
本节课讨论了两类含参数的二次函数最值问题:
(1)轴动区间定 (2)轴定区间动
核心思想仍然是判断对称轴与区间的相对位置,从中体会到数形结合思想、分类讨论思想。
小结:
