2018年高中数学北师大版必修2课件:第二章解析几何初步2-1-5平面直角坐标系中的距离公式课件(17张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第二章解析几何初步2-1-5平面直角坐标系中的距离公式课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 00:00:00 | ||
图片预览



文档简介
课件17张PPT。1.5平面直角坐标系中的距离公式
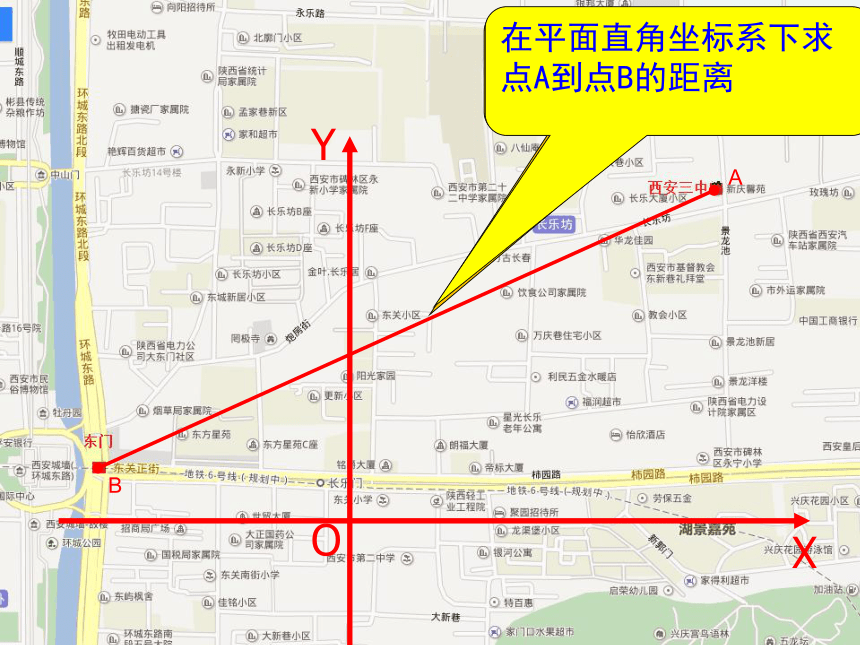
第一课时 两点间的距离公式 新课引入三中到东门的直线距离是多少?在平面直角坐标系下求点A到点B的距离AB了解平面直角坐标系中的两点间的距离公式的推导过程;
掌握平面直角坐标系中两点间的距离公式;
会用坐标法证明简单的几何问题。
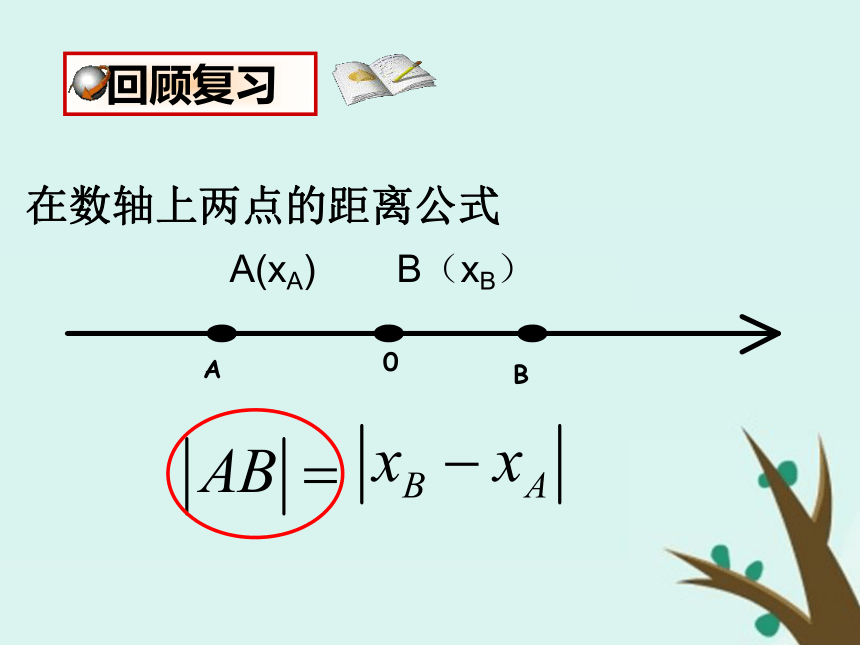
学习目标平面直角坐标系中两点间的距离公式在数轴上两点的距离公式A(xA) B(xB) 回顾复习 1. 在平面直角坐标系中,描出下列
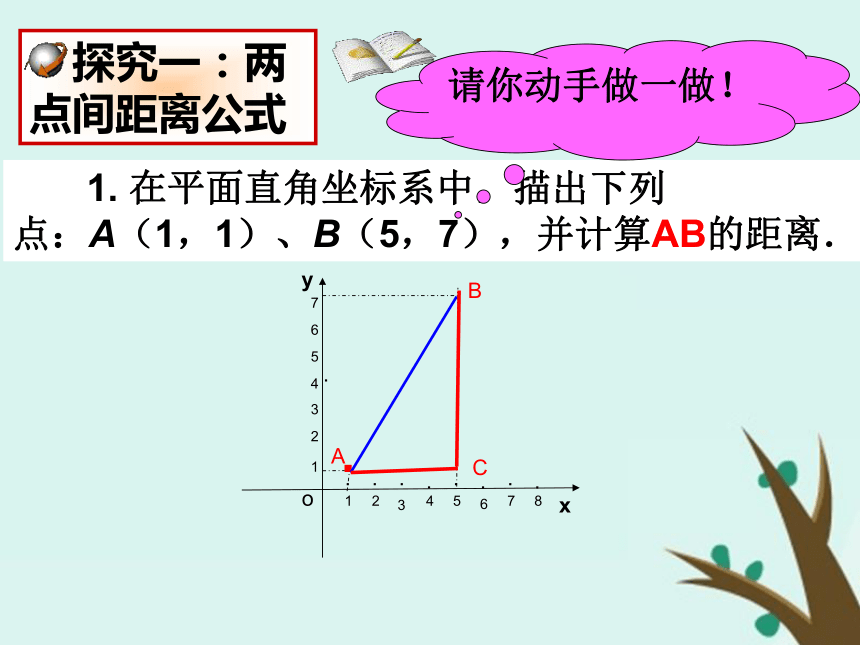
点:A(1,1)、B(5,7),并计算AB的距离. C 探究一:两点间距离公式请你动手做一做!
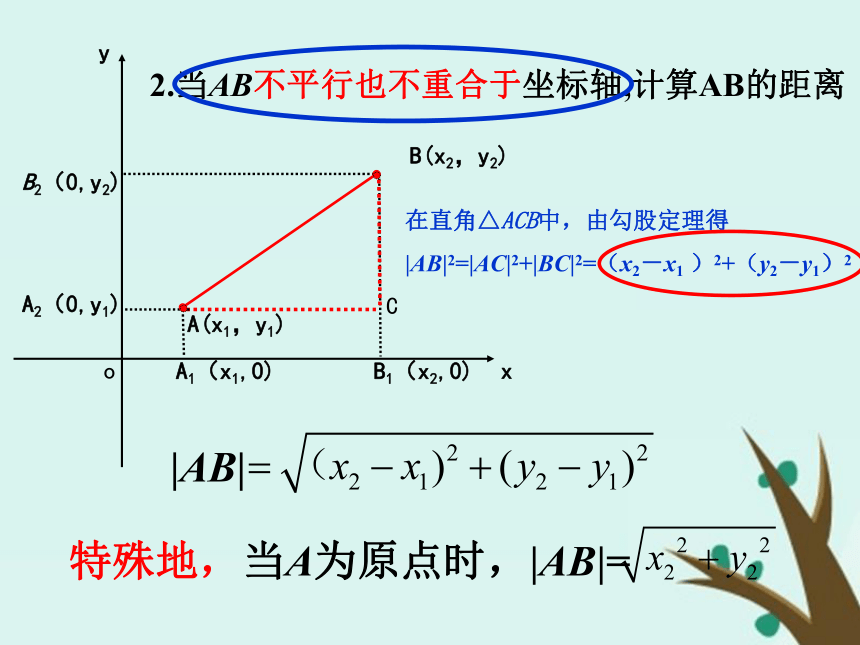
A1(x1,0)B1(x2,0)A2(0,y1)B2(0,y2)C在直角△ACB中,由勾股定理得
|AB|2=|AC|2+|BC|2=(x2-x1 )2+(y2-y1)2|AB|2.当AB不平行也不重合于坐标轴,计算AB的距离特殊地,当A为原点时,|AB|=当 平行于x轴时当 平行于y轴时3.当AB平行于坐标轴时4.当AB与坐标轴重合呢?
两点间的距离公式例1.已知点A(1,2),B(3,4),C(5,0),求证:△ABC是等腰三角形。证明:|AB|= |AC|= |BC|= 因为|AC|=|BC|,且A,B,C不共线, 所以△ABC是等腰三角形。 坐标法:就是通过建立坐标系,用代数方法解决几何问题,也就是将几何问题转化为代数问题,再通过一步步地计算来解决问题的方法. 探究二:坐标法用坐标法证题的步骤:(1)根据题设条件,在适当位置建立平面直角坐标系;
(2)设出未知坐标;
(3)根据题设条件推导出所需未知点的坐标,进而推导结论.例2、△ABC中,D是BC边上任意一点(D与B,C不重合)
且 ,求证:△ABC为等腰三角形。
证明:作AO⊥BC,垂足为O,以BC所在直线为X轴,以OA所在直线为Y轴,建立直角坐标系,
因为 则:1、探究范围:探究案2,3,4题
2、时间:5分钟
3、讨论及展示要求:
① 分享并汇总组内正确的解题方法
②讨论完请大家坐下,进行第一次纠错
③鼓励自由展示;
④鼓励自由点评,点评的时候要注意和同学的互动。
⑤点评和展示时,其他同学可进行补充、质疑,并给予加分。 合作探究1. 课堂小结 2.用坐标法证题的步骤: (1)根据题设条件,在适当位置建立平面直角坐标系;(2)设出未知坐标;(3)根据题设条件推导出所需未知点的坐标,进而推导结论. 布置作业2.完成031导学案,预习下一节内容1.(例2)△ABC中,D是BC边上任意一点(D与B,C不重合)
且 ,求证:△ABC为等腰三角形。
用其他建系的方法去证明,感受一下哪种方法更简单。Thank you!
掌握平面直角坐标系中两点间的距离公式;
会用坐标法证明简单的几何问题。
学习目标平面直角坐标系中两点间的距离公式在数轴上两点的距离公式A(xA) B(xB) 回顾复习 1. 在平面直角坐标系中,描出下列
点:A(1,1)、B(5,7),并计算AB的距离. C 探究一:两点间距离公式请你动手做一做!
A1(x1,0)B1(x2,0)A2(0,y1)B2(0,y2)C在直角△ACB中,由勾股定理得
|AB|2=|AC|2+|BC|2=(x2-x1 )2+(y2-y1)2|AB|2.当AB不平行也不重合于坐标轴,计算AB的距离特殊地,当A为原点时,|AB|=当 平行于x轴时当 平行于y轴时3.当AB平行于坐标轴时4.当AB与坐标轴重合呢?
两点间的距离公式例1.已知点A(1,2),B(3,4),C(5,0),求证:△ABC是等腰三角形。证明:|AB|= |AC|= |BC|= 因为|AC|=|BC|,且A,B,C不共线, 所以△ABC是等腰三角形。 坐标法:就是通过建立坐标系,用代数方法解决几何问题,也就是将几何问题转化为代数问题,再通过一步步地计算来解决问题的方法. 探究二:坐标法用坐标法证题的步骤:(1)根据题设条件,在适当位置建立平面直角坐标系;
(2)设出未知坐标;
(3)根据题设条件推导出所需未知点的坐标,进而推导结论.例2、△ABC中,D是BC边上任意一点(D与B,C不重合)
且 ,求证:△ABC为等腰三角形。
证明:作AO⊥BC,垂足为O,以BC所在直线为X轴,以OA所在直线为Y轴,建立直角坐标系,
因为 则:1、探究范围:探究案2,3,4题
2、时间:5分钟
3、讨论及展示要求:
① 分享并汇总组内正确的解题方法
②讨论完请大家坐下,进行第一次纠错
③鼓励自由展示;
④鼓励自由点评,点评的时候要注意和同学的互动。
⑤点评和展示时,其他同学可进行补充、质疑,并给予加分。 合作探究1. 课堂小结 2.用坐标法证题的步骤: (1)根据题设条件,在适当位置建立平面直角坐标系;(2)设出未知坐标;(3)根据题设条件推导出所需未知点的坐标,进而推导结论. 布置作业2.完成031导学案,预习下一节内容1.(例2)△ABC中,D是BC边上任意一点(D与B,C不重合)
且 ,求证:△ABC为等腰三角形。
用其他建系的方法去证明,感受一下哪种方法更简单。Thank you!
