2018年高中数学北师大版必修2课件:第二章解析几何初步2-3-1空间直角坐标系的建立课件(34张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第二章解析几何初步2-3-1空间直角坐标系的建立课件(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 22:22:37 | ||
图片预览









文档简介
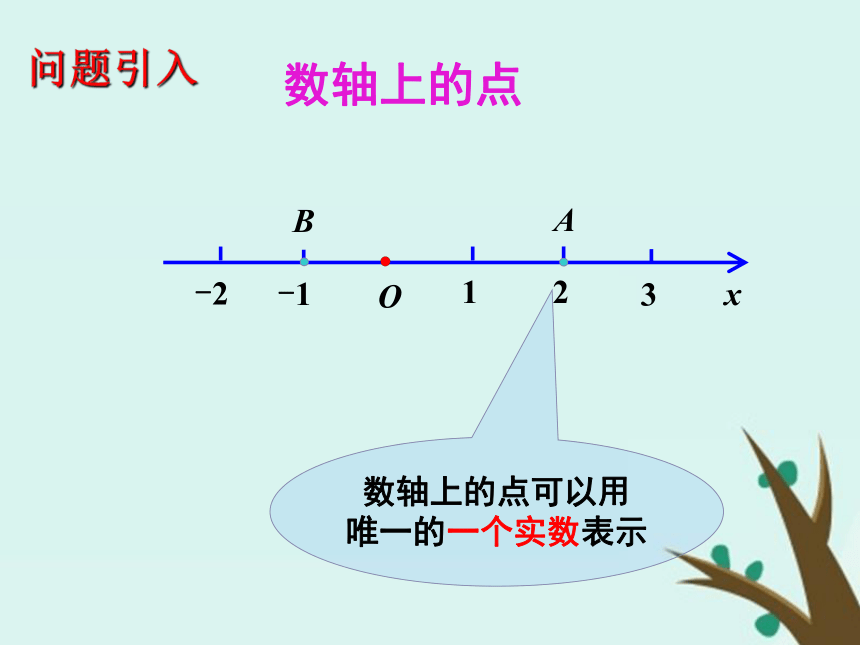
课件34张PPT。空间直角坐标系问题引入 1.数轴Ox上的点M,用代数的方法怎样表示呢? 2.直角坐标平面上的点M,怎样表示呢? 数轴Ox上的点M,可用与它对应的实数x表示; 直角坐标平面上的点M,可用一对有序实数(x,y)表示.xO数轴上的点可以用
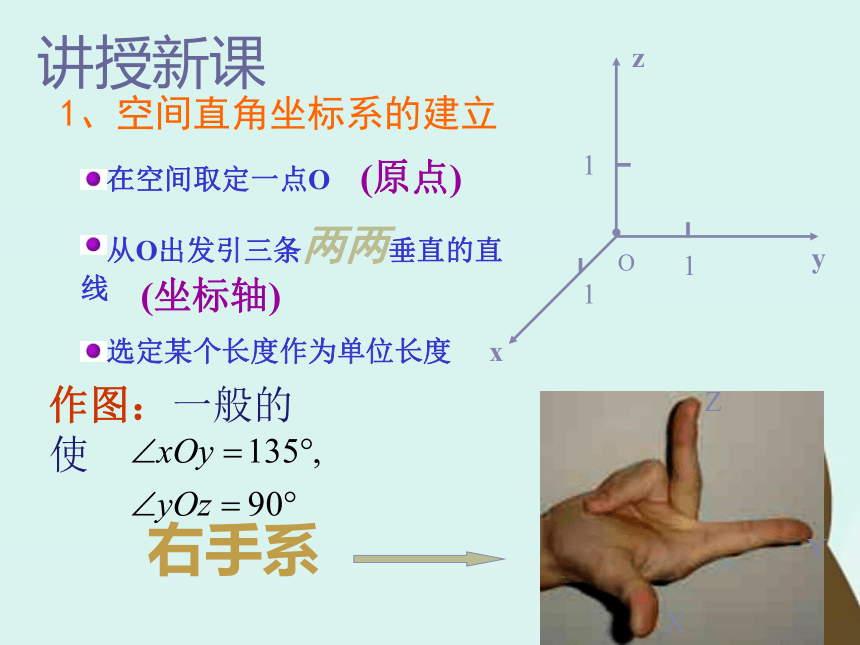
唯一的一个实数表示-1-2123AB数轴上的点问题引入xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示点平面坐标系中的点问题引入1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)讲授新课作图: 通过每两个坐标轴的
平面叫 坐标平面,二、讲授新课O为坐标原点x轴,y轴,z轴叫 坐标轴面面面空间直角坐标系共有八个卦限2、空间直角坐标系的划分?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz M点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。XY x称为点P的x坐标PxPzx z yPPyy称为点P的y坐标z称为点P的z坐标反之:(x,y,z)对应唯一的点P 空间的点P有序数组二、空间中点的坐标二、空间中点的坐标有序实数组(x,y,z)叫做点P在此空间
直角坐标系中的坐标,记作P(x,y,z)
其中x叫做点P的横坐标,y叫做点P的
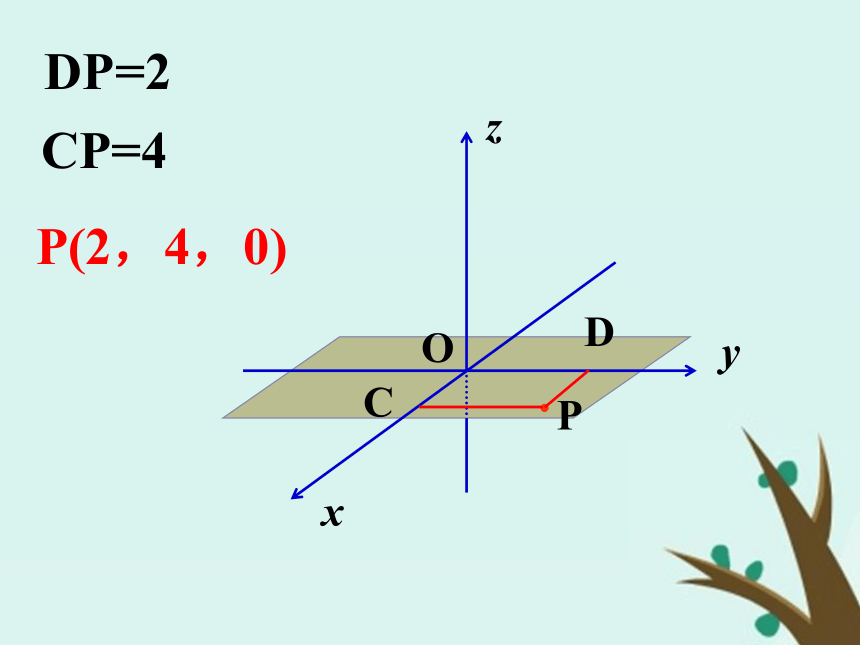
纵坐标,z叫做点P的竖坐标POy xzCDDP=2CP=4P(2,4,0)POy xzP′CDDP′=2CP′=4P(2,4,5)P′P=5′Oy xzP′PD=2PC=4P(2,4,-5)P′P= - 5三、空间中点的射影点与对称点坐标1.点P(x , y , z) 在下列坐标平面中的射影点为:
(1)在xoy平面射影点为P1__________;
(2)在xoz平面射影点为P2__________;
(3)在yoz平面射影点为P3__________;
;
(x,y,0)(x,0,z)(0,y,z)关于坐标平面对称2点P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)xoz平面对称的点P3为__________;
关于谁对称谁不变(x,y,-z)(-x,y,z)(x, -y, z)对称点3.点P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变在空间坐标系中画出空间中的点A(0,-1,2)
B(1,2,3)Bxoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点规律总结:B设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?空间两点中点坐标公式3.2 空间两点间的距离公式两点间距离公式类比猜想O(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:P`(x,y,0)空间两点间的距离公式O(1) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:NMH1、在空间直角坐标系中标出求A、B两点,并求出它们之间的距离:
(1) A(2,3,5) B(3,1,4)
(2) A(6,0,1) B(3,5,7) 练习课本P138 练习12、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等.课本P138 练习2解设P点坐标为所求点为MN3、如图,正方体OABC-D`A`B`C`的棱长为a,|AN|=2|CN|,|BM|=2|MC`|,求MN的长. 练习课本P138 练习4解原结论成立.
唯一的一个实数表示-1-2123AB数轴上的点问题引入xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示点平面坐标系中的点问题引入1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)讲授新课作图: 通过每两个坐标轴的
平面叫 坐标平面,二、讲授新课O为坐标原点x轴,y轴,z轴叫 坐标轴面面面空间直角坐标系共有八个卦限2、空间直角坐标系的划分?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz M点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。XY x称为点P的x坐标PxPzx z yPPyy称为点P的y坐标z称为点P的z坐标反之:(x,y,z)对应唯一的点P 空间的点P有序数组二、空间中点的坐标二、空间中点的坐标有序实数组(x,y,z)叫做点P在此空间
直角坐标系中的坐标,记作P(x,y,z)
其中x叫做点P的横坐标,y叫做点P的
纵坐标,z叫做点P的竖坐标POy xzCDDP=2CP=4P(2,4,0)POy xzP′CDDP′=2CP′=4P(2,4,5)P′P=5′Oy xzP′PD=2PC=4P(2,4,-5)P′P= - 5三、空间中点的射影点与对称点坐标1.点P(x , y , z) 在下列坐标平面中的射影点为:
(1)在xoy平面射影点为P1__________;
(2)在xoz平面射影点为P2__________;
(3)在yoz平面射影点为P3__________;
;
(x,y,0)(x,0,z)(0,y,z)关于坐标平面对称2点P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)xoz平面对称的点P3为__________;
关于谁对称谁不变(x,y,-z)(-x,y,z)(x, -y, z)对称点3.点P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变在空间坐标系中画出空间中的点A(0,-1,2)
B(1,2,3)Bxoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点规律总结:B设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?空间两点中点坐标公式3.2 空间两点间的距离公式两点间距离公式类比猜想O(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:P`(x,y,0)空间两点间的距离公式O(1) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:NMH1、在空间直角坐标系中标出求A、B两点,并求出它们之间的距离:
(1) A(2,3,5) B(3,1,4)
(2) A(6,0,1) B(3,5,7) 练习课本P138 练习12、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等.课本P138 练习2解设P点坐标为所求点为MN3、如图,正方体OABC-D`A`B`C`的棱长为a,|AN|=2|CN|,|BM|=2|MC`|,求MN的长. 练习课本P138 练习4解原结论成立.
