2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(18张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 396.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 22:28:58 | ||
图片预览





文档简介
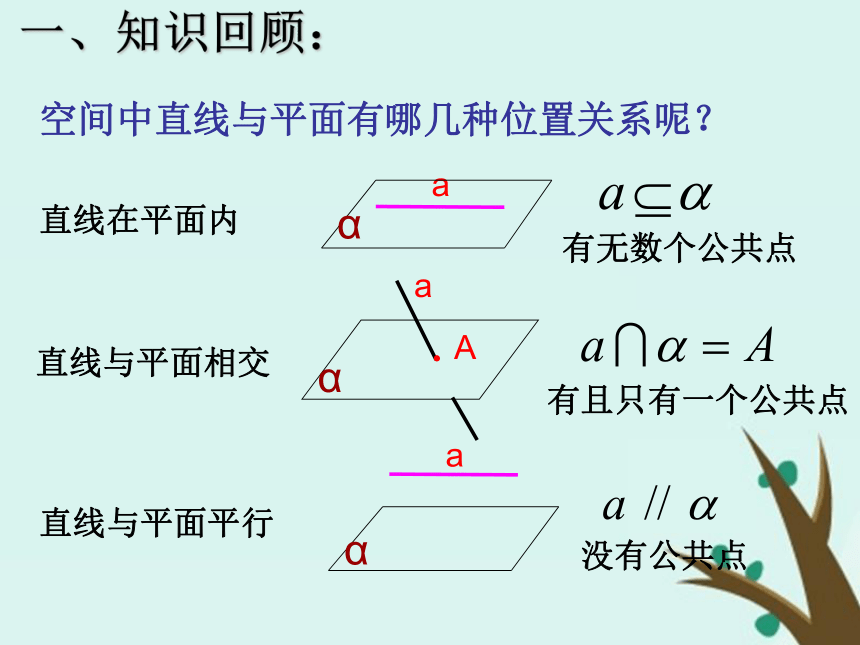
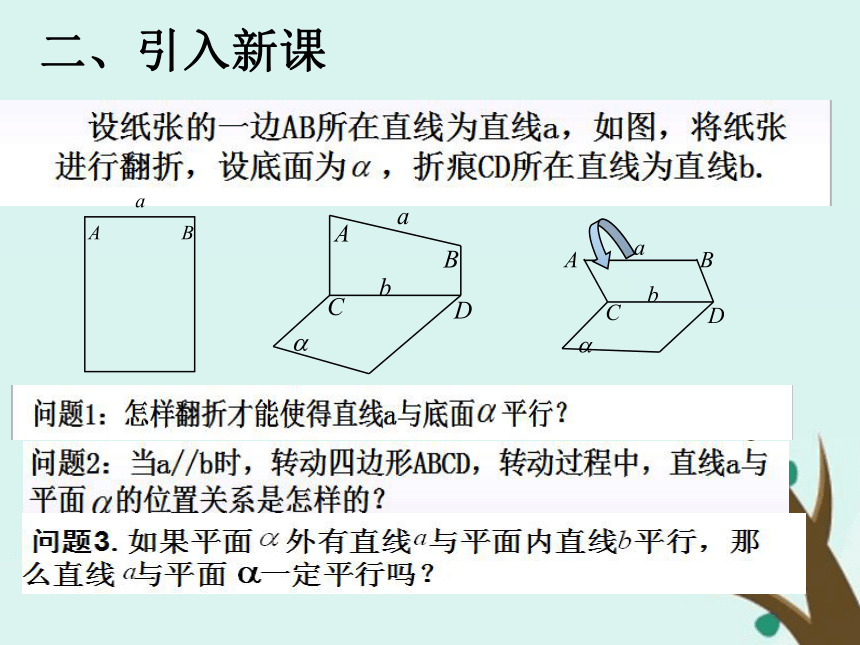
课件18张PPT。平行关系的判定一、知识回顾:空间中直线与平面有哪几种位置关系呢?直线在平面内 直线与平面相交直线与平面平行有无数个公共点有且只有一个公共点没有公共点二、引入新课三、解决问题 平面外的一条直线和此平面内的一条直线平行,则该直线和此平面平行.直线和平面平行的判定定理:四、新知讲解 五、随堂练习
正确的个数有( 个 例1 已知:空间四边形ABCD 中,E,F 分别是AB,AD 的中点。
求证:EF//平面BCD.分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连接BD立刻就清楚了。
六、典型例题例1 已知:空间四边形ABCD 中,E,F分别是
AB,AD 的中点.
求证:EF//平面BCD. 证明:连接BD.因为E,F分别是AB,
AD 的中点,所以EF//BDAEFBDC______________.EF//平面BCDABCDEFPABCDEMN例2:在四棱锥P—ABCD中,底面ABCD为平行四边形,N为PB 的中点,E为AD中点。
求证:EN//平面PDC证明:取PC的中点为M,连接MN,MD,EN.
M,N分别为PC,PB的中点,则MN//BC且
MN= BC.(三角形中位线定理)
ABCD是平行四边形,且E为AD的中点.
ED//BC且ED= BC.故MN//ED且MN=ED,则四边形ENMD为平行四边形
EN//MD
又
由直线与平面平行的判定定理得:
EN//平面PDC例2.变式3、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM 变式4.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 .1、如图,已知在三棱柱ABC——A1B1C1中,D是AC的中点。
求证:AB1//平面DBC1P练一练2.注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.关键是找平行线方法一:通过相似找线线平行,常见的有三角形的中位线定理、平行线分线段成比例的逆命题 ;
方法二:平行四边形的平行关系。4.数学思想方法:转化与化归的思想 通过直线间的平行,推证直线与平面平行,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题).
正确的个数有( 个 例1 已知:空间四边形ABCD 中,E,F 分别是AB,AD 的中点。
求证:EF//平面BCD.分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连接BD立刻就清楚了。
六、典型例题例1 已知:空间四边形ABCD 中,E,F分别是
AB,AD 的中点.
求证:EF//平面BCD. 证明:连接BD.因为E,F分别是AB,
AD 的中点,所以EF//BDAEFBDC______________.EF//平面BCDABCDEFPABCDEMN例2:在四棱锥P—ABCD中,底面ABCD为平行四边形,N为PB 的中点,E为AD中点。
求证:EN//平面PDC证明:取PC的中点为M,连接MN,MD,EN.
M,N分别为PC,PB的中点,则MN//BC且
MN= BC.(三角形中位线定理)
ABCD是平行四边形,且E为AD的中点.
ED//BC且ED= BC.故MN//ED且MN=ED,则四边形ENMD为平行四边形
EN//MD
又
由直线与平面平行的判定定理得:
EN//平面PDC例2.变式3、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM 变式4.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 .1、如图,已知在三棱柱ABC——A1B1C1中,D是AC的中点。
求证:AB1//平面DBC1P练一练2.注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.关键是找平行线方法一:通过相似找线线平行,常见的有三角形的中位线定理、平行线分线段成比例的逆命题 ;
方法二:平行四边形的平行关系。4.数学思想方法:转化与化归的思想 通过直线间的平行,推证直线与平面平行,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题).
