2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(15张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 127.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 22:29:18 | ||
图片预览

文档简介
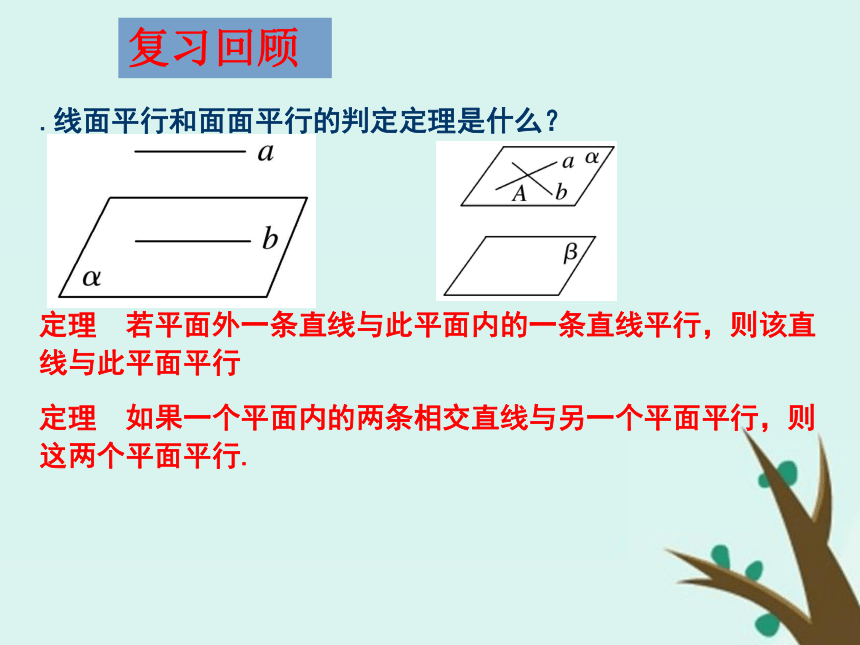
课件15张PPT。 平行关系的性质复习回顾.线面平行和面面平行的判定定理是什么?
定理 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
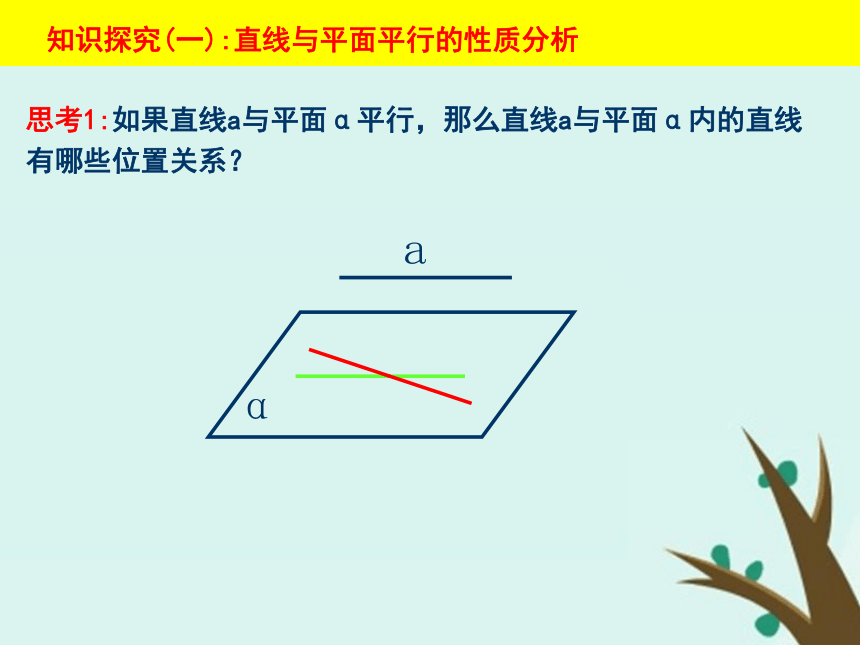
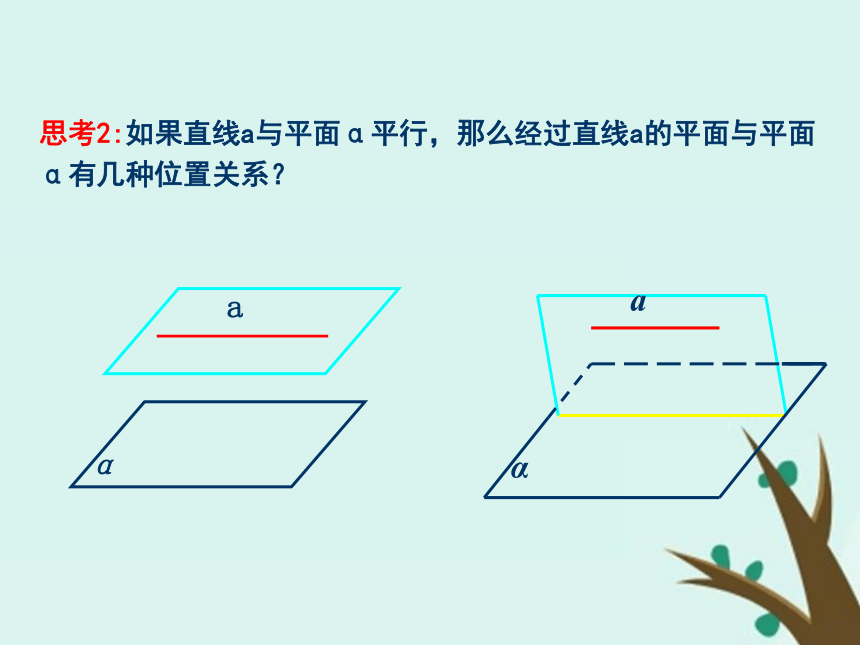
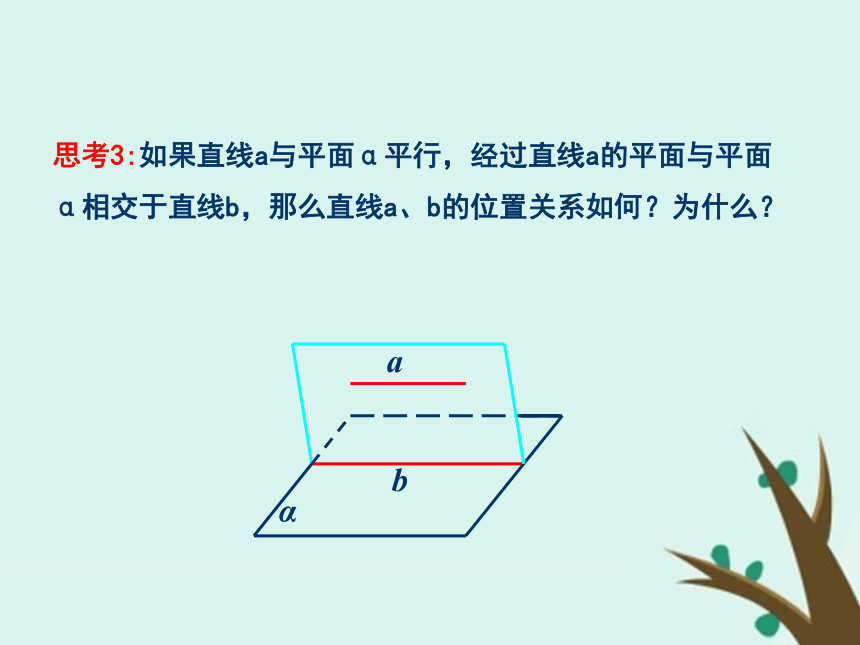
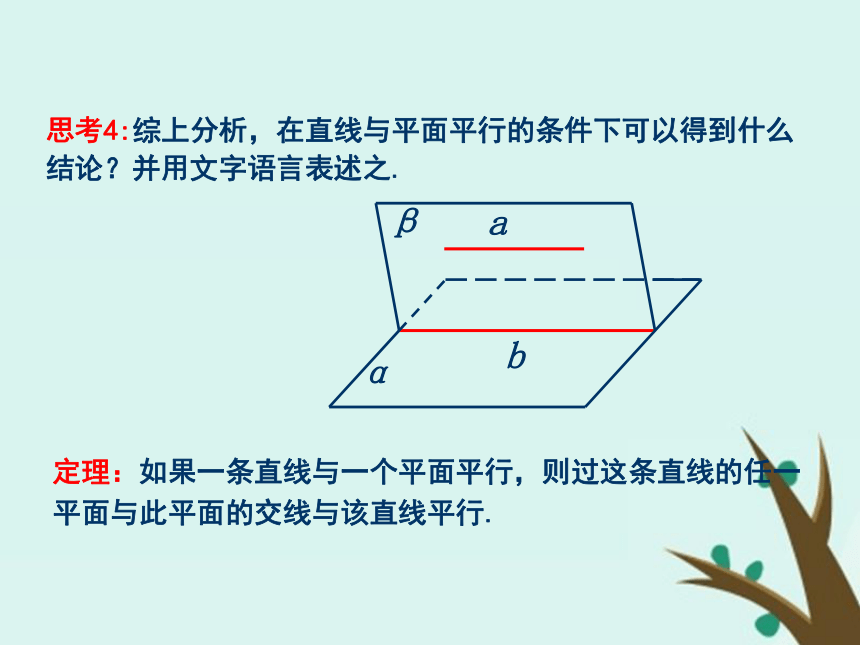
知识探究(一):直线与平面平行的性质分析 思考1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?思考2:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?思考3:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?思考4:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
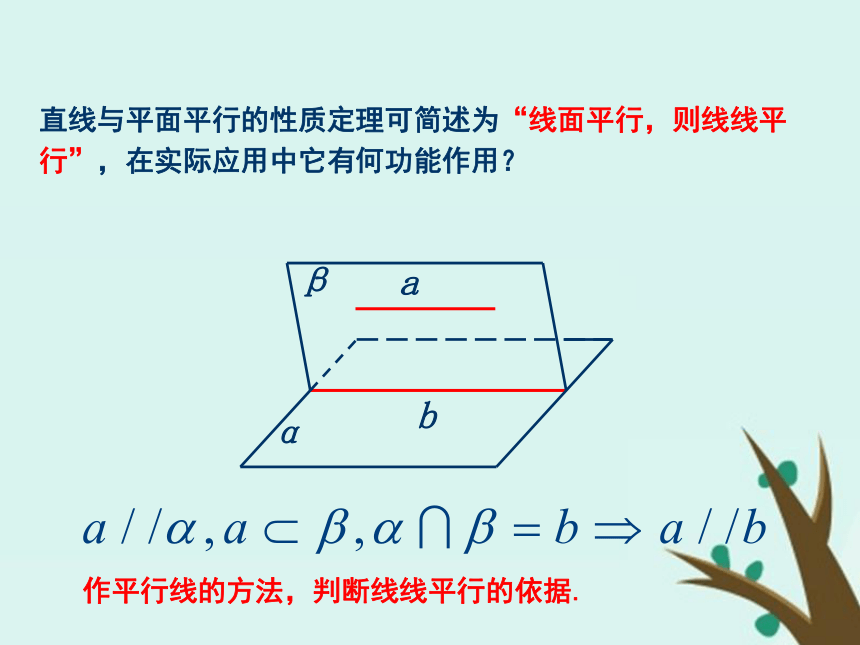
直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 例1.已知:如图,AB//平面β,AC//BD,
且AC、BD与 β分别相 交于点C, D.
求证:AC=BD.证明:∵AB∥β ,平面AD∩β=CD∴AB∥CD∴四边形ABCD是平行四边形∴AC=BD例题解析∵AC ∥BD,∴AC与BD确定一个平面AD 例2.在四面体ABCD中,E、F分别是AB、 AC的中点,过直线EF作平面α,分别交BD, CD于M、N,求证:EF∥MN.例题解析知识探究(二):平面与平面平行的性质分析 思考6:若 ,则直线l与平面β的位置关系如何? “若面面平行,则线面平行”思考7:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.“若面面平行,则线线平行”例3.如下图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,AC∩β=B,DF∩β=E.
求证:
同理,
证明:连结AF交β于M,连结BM、EM,BE.∵β∥γ,平面ACF分别交β、
γ于BM、CF,∴BM∥CF.
∴ 1.直线与平面平行和平面与平面平行的性质:
2.数学思想方法:转化的思想知识小结
定理 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
知识探究(一):直线与平面平行的性质分析 思考1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?思考2:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?思考3:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?思考4:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 例1.已知:如图,AB//平面β,AC//BD,
且AC、BD与 β分别相 交于点C, D.
求证:AC=BD.证明:∵AB∥β ,平面AD∩β=CD∴AB∥CD∴四边形ABCD是平行四边形∴AC=BD例题解析∵AC ∥BD,∴AC与BD确定一个平面AD 例2.在四面体ABCD中,E、F分别是AB、 AC的中点,过直线EF作平面α,分别交BD, CD于M、N,求证:EF∥MN.例题解析知识探究(二):平面与平面平行的性质分析 思考6:若 ,则直线l与平面β的位置关系如何? “若面面平行,则线面平行”思考7:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.“若面面平行,则线线平行”例3.如下图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,AC∩β=B,DF∩β=E.
求证:
同理,
证明:连结AF交β于M,连结BM、EM,BE.∵β∥γ,平面ACF分别交β、
γ于BM、CF,∴BM∥CF.
∴ 1.直线与平面平行和平面与平面平行的性质:
2.数学思想方法:转化的思想知识小结
