2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(14张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 22:31:45 | ||
图片预览





文档简介
课件14张PPT。直线与平面垂直的性质
1.理解直线与平面垂直的性质定理,并能用文字、符号和图形语言描述该定理.
2.掌握证明直线与平面垂直的性质定理的证明方法.
3.了解垂直的判定定理和性质定理的相互联系,能运用性质定理解决一些简单问题.
4.通过定理的学习,培养空间想象、推理论证、几何直观能力.
【重点】直线与平面垂直的性质定理
【难点】反证法的学习和掌握,性质定理的证明及应用.
生活中的数学1.直线和平面的位置关系2.直线与平面垂直的方法
?直线和平面垂直的定义:
如果一条直线和平面内的 任何一条直线都垂直,那么称这条直线和这个平面垂直。
ɑ为平面α内任一直线
?直线和平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么称这条直线垂直于这个平面.
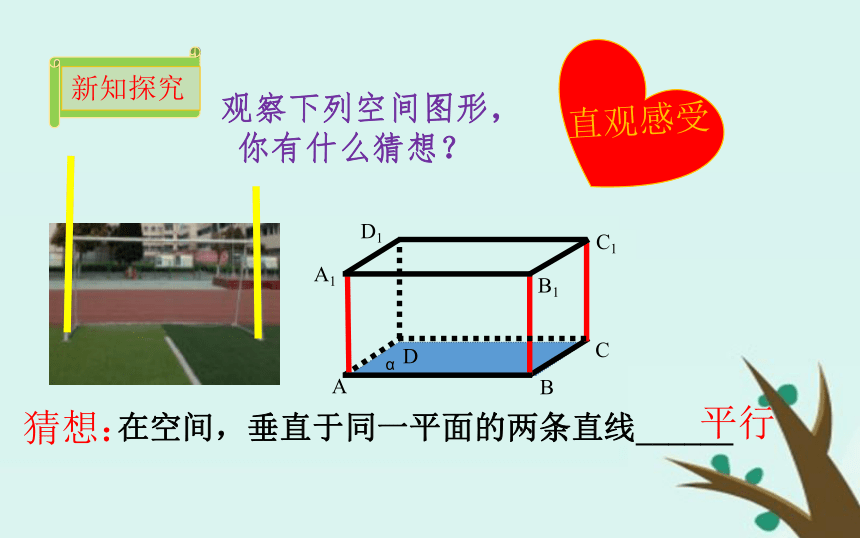
aαɑbA性质平行 在空间是否有相同的或类似的结论呢?在空间,垂直于同一平面的两条直线______平行观察下列空间图形,
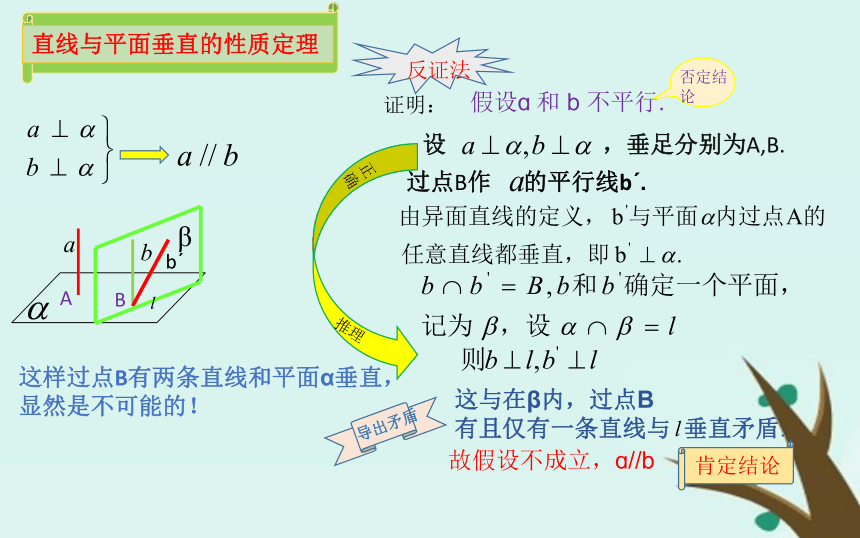
你有什么猜想?猜想:AB 假设ɑ 和 b 不平行.设 ,垂足分别为A,B.这样过点B有两条直线和平面α垂直,
显然是不可能的! 故假设不成立,ɑ//b肯定结论证明:这与在β内,过点B
有且仅有一条直线与 垂直矛盾. 过点B作 的平行线bˊ.文字语言:
如果两条直线同垂直于一个平面,那么这两条直线平行。
符号语言 图形语言:
作用:
证明两条直线平行
定理证明方法:
反正法线面垂直的性质定理??例1.如图,在正方体ABCD-AˊBˊCˊDˊ中,AD',A'D分别为三条面对角线,AˊC为一条体对角线,MN⊥平面ADC.
求证:MN//ADˊ.证明:证题原则:从已知想性质,从求证想判定。例2: 如图,AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.∵ A D⊥α,BC⊥α∴AD//BC,AD⊥DC∵AD//BC,∴AD与BC在平面ABCD内.证明:∴AB//CD∵PA⊥AB∴PA⊥CD∴CD⊥平面PAD又AD⊥DCD3.下列说法正确的是________(1),(3),(4)2.如图,如果MC 菱形ABCD所在平面,那么MA与BD的位置关系是( )DA B CMA.平行 B.垂直相交
C.异面且垂直 D.相交但不垂直 C 1、知识:
2、数学方法
反证法 类比探究
3.思想方法
作业:1.P42 习题1-6 A组第7题.2.B组第1题
谢谢各位老师和同学
1.理解直线与平面垂直的性质定理,并能用文字、符号和图形语言描述该定理.
2.掌握证明直线与平面垂直的性质定理的证明方法.
3.了解垂直的判定定理和性质定理的相互联系,能运用性质定理解决一些简单问题.
4.通过定理的学习,培养空间想象、推理论证、几何直观能力.
【重点】直线与平面垂直的性质定理
【难点】反证法的学习和掌握,性质定理的证明及应用.
生活中的数学1.直线和平面的位置关系2.直线与平面垂直的方法
?直线和平面垂直的定义:
如果一条直线和平面内的 任何一条直线都垂直,那么称这条直线和这个平面垂直。
ɑ为平面α内任一直线
?直线和平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么称这条直线垂直于这个平面.
aαɑbA性质平行 在空间是否有相同的或类似的结论呢?在空间,垂直于同一平面的两条直线______平行观察下列空间图形,
你有什么猜想?猜想:AB 假设ɑ 和 b 不平行.设 ,垂足分别为A,B.这样过点B有两条直线和平面α垂直,
显然是不可能的! 故假设不成立,ɑ//b肯定结论证明:这与在β内,过点B
有且仅有一条直线与 垂直矛盾. 过点B作 的平行线bˊ.文字语言:
如果两条直线同垂直于一个平面,那么这两条直线平行。
符号语言 图形语言:
作用:
证明两条直线平行
定理证明方法:
反正法线面垂直的性质定理??例1.如图,在正方体ABCD-AˊBˊCˊDˊ中,AD',A'D分别为三条面对角线,AˊC为一条体对角线,MN⊥平面ADC.
求证:MN//ADˊ.证明:证题原则:从已知想性质,从求证想判定。例2: 如图,AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.∵ A D⊥α,BC⊥α∴AD//BC,AD⊥DC∵AD//BC,∴AD与BC在平面ABCD内.证明:∴AB//CD∵PA⊥AB∴PA⊥CD∴CD⊥平面PAD又AD⊥DCD3.下列说法正确的是________(1),(3),(4)2.如图,如果MC 菱形ABCD所在平面,那么MA与BD的位置关系是( )DA B CMA.平行 B.垂直相交
C.异面且垂直 D.相交但不垂直 C 1、知识:
2、数学方法
反证法 类比探究
3.思想方法
作业:1.P42 习题1-6 A组第7题.2.B组第1题
谢谢各位老师和同学
