江苏省仪征市第三中学2018年七年级数学第6章《平面图形的认识一》同步提高测试(含答案)
文档属性
| 名称 | 江苏省仪征市第三中学2018年七年级数学第6章《平面图形的认识一》同步提高测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 284.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-12 00:00:00 | ||
图片预览

文档简介
七年级数学第6章《平面图形的认识一》同步提高测试
一、选择题:
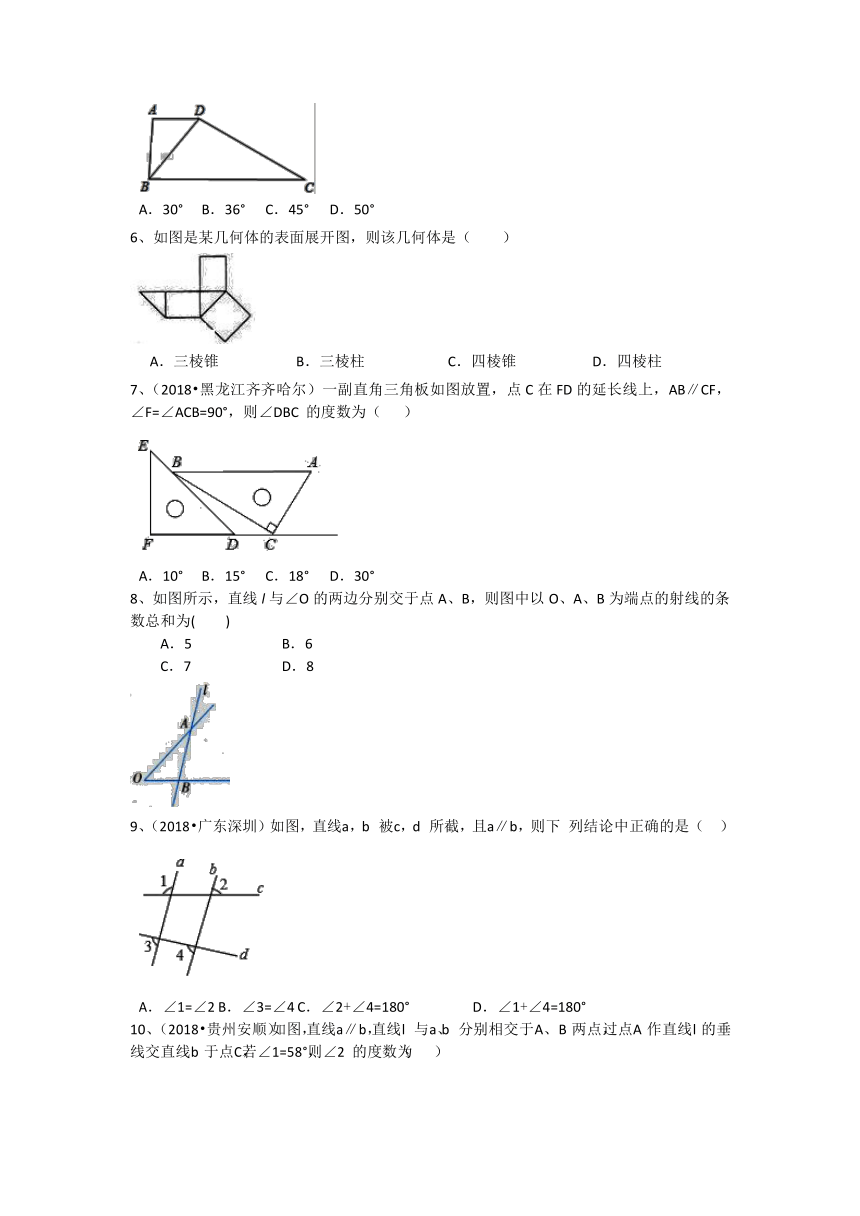
1、(2018?浙江衢州)如图,直线 a,b 被直线 c 所截,那么∠1 的 同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
3、下列图形中不是正方体的平面展开图的是( )
A. B.
C. D.
4、(2018?广东广州)如图,直线 AD,BE 被直线 BF 和 AC 所截,则∠1 的同位角和∠5 的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
5、(2018?湖北江汉)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,则∠DBC 的度数是( )
A.30° B.36° C.45° D.50°
6、如图是某几何体的表面展开图,则该几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
7、(2018?黑龙江齐齐哈尔)一副直角三角板如图放置,点 C在 FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC 的度数为( )
A.10° B.15° C.18° D.30°
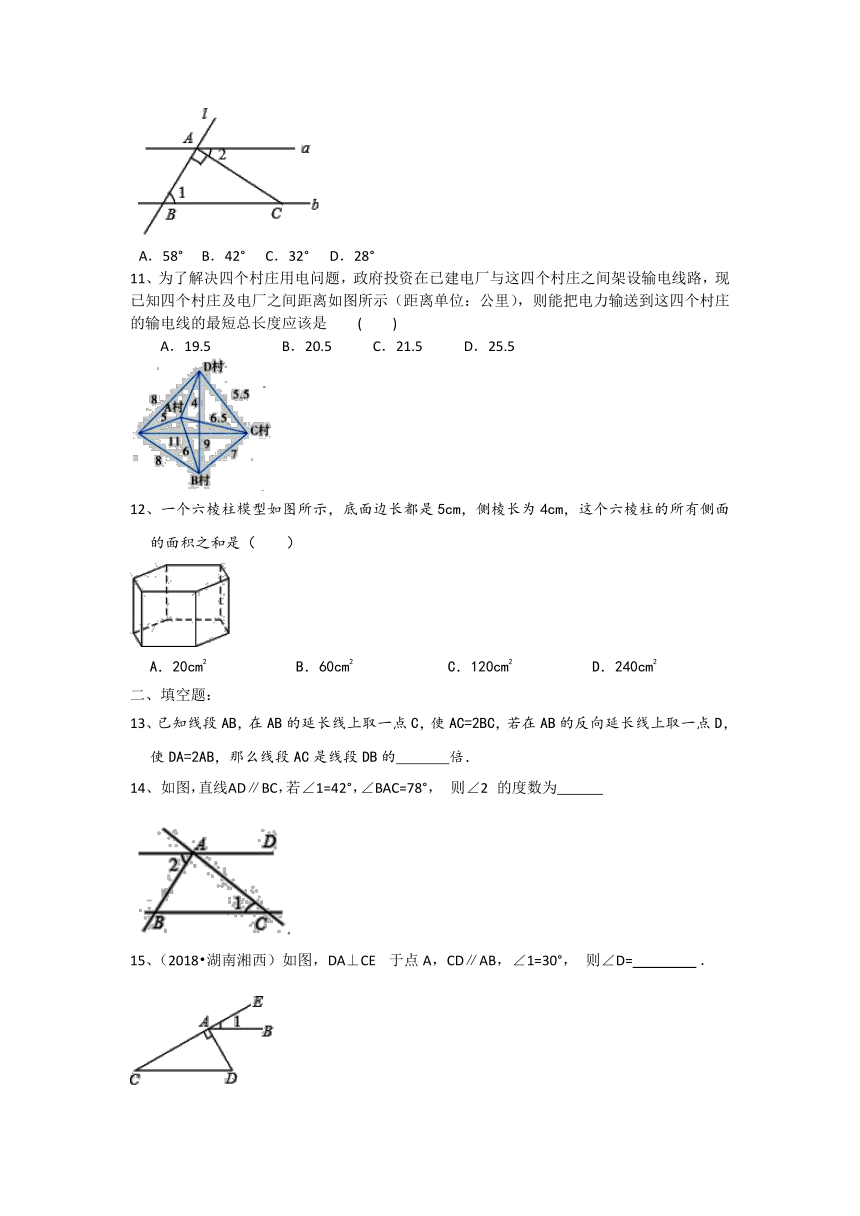
8、如图所示,直线l与∠O的两边分别交于点A、B,则图中以O、A、B为端点的射线的条数总和为( )
A.5 B.6
C.7 D.8
9、(2018?广东深圳)如图,直线 a,b 被 c,d 所截,且 a∥b,则下 列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=180° D.∠1+∠4=180°
10、(2018?贵州安顺)如图,直线 a∥b,直线 l 与 a、b 分别相交于 A、B 两点,过点 A 作直线 l 的垂线交直线 b 于点 C,若∠1=58°,则∠2 的度数为( )
A.58° B.42° C.32° D.28°
11、为了解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路,现已知四个村庄及电厂之间距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线的最短总长度应该是 ( )
A.19.5 B.20.5 C.21.5 D.25.5
12、一个六棱柱模型如图所示,底面边长都是5cm,侧棱长为4cm,这个六棱柱的所有侧面的面积之和是( )
A.20cm2 B.60cm2 C.120cm2 D.240cm2
二、填空题:
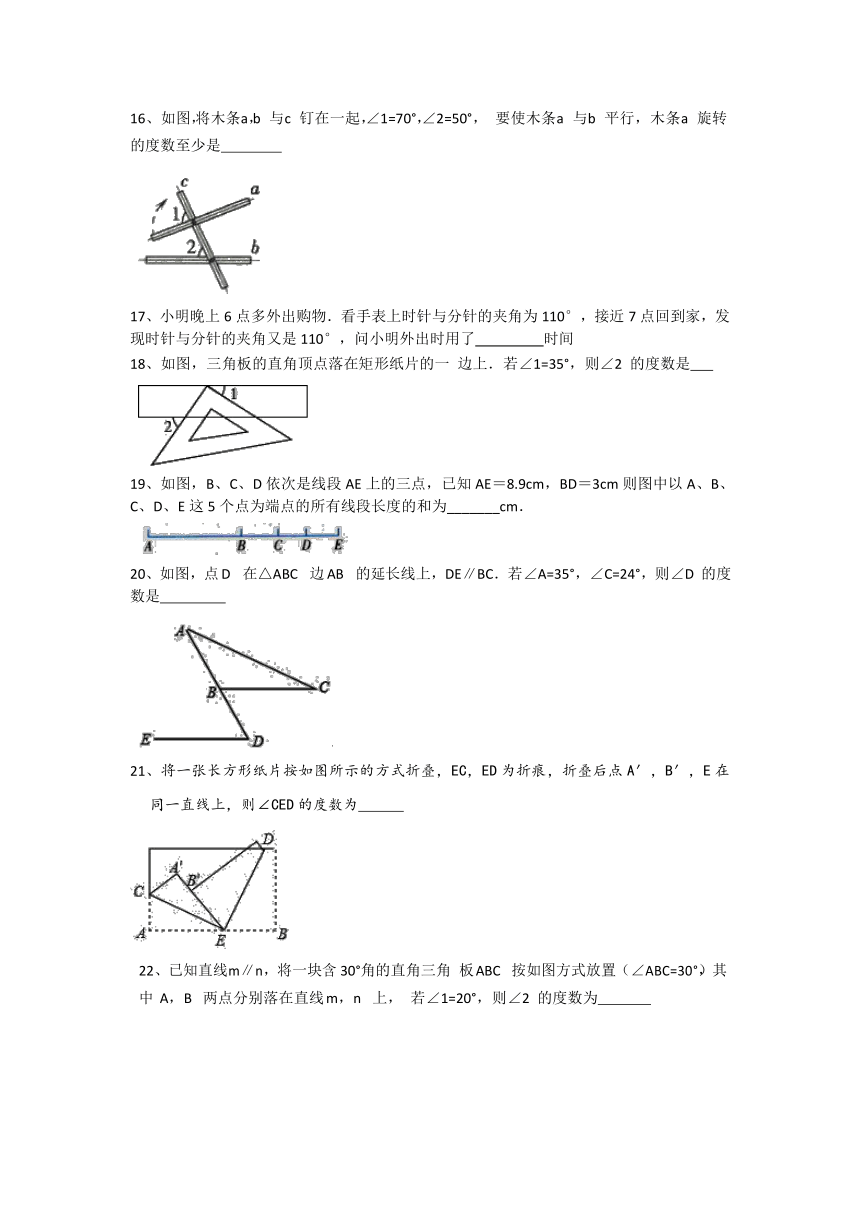
13、已知线段AB,在AB的延长线上取一点C,使AC=2BC,若在AB的反向延长线上取一点D,使DA=2AB,那么线段AC是线段DB的 倍.
14、如图,直线 AD∥BC,若∠1=42°,∠BAC=78°, 则∠2 的度数为
15、(2018?湖南湘西)如图,DA⊥CE 于点 A,CD∥AB,∠1=30°, 则∠D= .
16、如图,将木条 a,b 与 c 钉在一起,∠1=70°,∠2=50°, 要使木条 a 与 b 平行,木条 a 旋转的度数至少是
17、小明晚上6点多外出购物.看手表上时针与分针的夹角为110°,接近7点回到家,发现时针与分针的夹角又是110°,问小明外出时用了 时间
18、如图,三角板的直角顶点落在矩形纸片的一 边上.若∠1=35°,则∠2 的度数是
19、如图,B、C、D依次是线段AE上的三点,已知AE=8.9cm,BD=3cm则图中以A、B、C、D、E这5个点为端点的所有线段长度的和为_______cm.
20、如图,点 D 在△ABC 边 AB 的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D 的度数是
21、将一张长方形纸片按如图所示的方式折叠,EC,ED为折痕,折叠后点A′,B′,E在同一直线上,则∠CED的度数为
22、已知直线 m∥n,将一块含 30°角的直角三角 板 ABC 按如图方式放置(∠ABC=30°),其中 A,B 两点分别落在直线 m,n 上, 若∠1=20°,则∠2 的度数为
三、解答题:
23、如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
24、如图,AB∥CD,点 E 在线段 BC 上,CD=CE.若∠ABC=30°, 则∠D的度数为多少?
25、如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
26、设有甲、乙、丙三人,他们的步行速度相同,骑车速度也相同,骑车的速度为步行速度的3倍,现甲自A地去B地,乙、丙则从B地去A地,双方同时出发,出发时,甲、乙为步行,丙骑车,途中,当甲、丙相遇时,丙将车给甲骑,自己改为步行,三人仍按各自原有方向继续前进;当甲、乙相遇时,甲将车给乙骑,自己又步行,三人仍按各自方向继续前进,问:三人之中谁最选到达自己的目的地?谁最后到达目的地?
27、(1)如图①,已知点A,B位于直线MN的两侧,请在直线MN上找一点P,使PA+PB最小,并说明依据.
(2)如图②,动点O在直线MN上运动,连接AO,分别作∠AOM,∠AON的平分线OC,OD,∠COD的度数是否发生变化?若不变,求出∠COD的度数;若变化,说明理由.
一、选择题:
1、C
2、B
3、C
4、B
5、D
6、B
7、B
8、D
9、B
10、C
11、B
12、C
二、填空题:
13、2/3
14、60°
15、60°
16、20°
17、40分钟
18、55°
19、41.6
20、59°
21、90°
22、50°
三、解答题:
23、(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
24、∵AB∥CD,
∴∠C=∠ABC=30°, 又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即 30°+2∠D=180°,
∴∠D=75°.
25、(1)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∵∠BOC=50°,∠BOA=80°,
∴∠BOD=25°,∠BOE=40°,
∴∠DOE=25°+40°=65°;
(2)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∵∠AOC=150°,
∴∠DOE=∠DOB+∠EOB=(∠BOC+∠BOA)=∠AOC=75°;
(3)∠DOE=∠AOC;
理由是:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∴∠DOE=∠DOB+∠EOB=(∠BOC+∠BOA)=∠AOC.
26、丙最先到达目的地,甲最后到达目的地.
27、(1)连接AB交MN于点P,则P就是所求的点(图略).依据:两点之间线段最短.
(2)∠COD的度数不会发生变化.
∵OC是∠AOM的平分线,
∴∠COA=∠AOM.
∵OD是∠AON的平分线,
∴∠AOD=∠AON.
∵∠AOM+∠AON=180°,
∴∠COD=∠COA+∠AOD=∠AOM+∠AON=(∠AOM+∠AON)=90°.
一、选择题:
1、(2018?浙江衢州)如图,直线 a,b 被直线 c 所截,那么∠1 的 同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
3、下列图形中不是正方体的平面展开图的是( )
A. B.
C. D.
4、(2018?广东广州)如图,直线 AD,BE 被直线 BF 和 AC 所截,则∠1 的同位角和∠5 的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
5、(2018?湖北江汉)如图,AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,则∠DBC 的度数是( )
A.30° B.36° C.45° D.50°
6、如图是某几何体的表面展开图,则该几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
7、(2018?黑龙江齐齐哈尔)一副直角三角板如图放置,点 C在 FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC 的度数为( )
A.10° B.15° C.18° D.30°
8、如图所示,直线l与∠O的两边分别交于点A、B,则图中以O、A、B为端点的射线的条数总和为( )
A.5 B.6
C.7 D.8
9、(2018?广东深圳)如图,直线 a,b 被 c,d 所截,且 a∥b,则下 列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=180° D.∠1+∠4=180°
10、(2018?贵州安顺)如图,直线 a∥b,直线 l 与 a、b 分别相交于 A、B 两点,过点 A 作直线 l 的垂线交直线 b 于点 C,若∠1=58°,则∠2 的度数为( )
A.58° B.42° C.32° D.28°
11、为了解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路,现已知四个村庄及电厂之间距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线的最短总长度应该是 ( )
A.19.5 B.20.5 C.21.5 D.25.5
12、一个六棱柱模型如图所示,底面边长都是5cm,侧棱长为4cm,这个六棱柱的所有侧面的面积之和是( )
A.20cm2 B.60cm2 C.120cm2 D.240cm2
二、填空题:
13、已知线段AB,在AB的延长线上取一点C,使AC=2BC,若在AB的反向延长线上取一点D,使DA=2AB,那么线段AC是线段DB的 倍.
14、如图,直线 AD∥BC,若∠1=42°,∠BAC=78°, 则∠2 的度数为
15、(2018?湖南湘西)如图,DA⊥CE 于点 A,CD∥AB,∠1=30°, 则∠D= .
16、如图,将木条 a,b 与 c 钉在一起,∠1=70°,∠2=50°, 要使木条 a 与 b 平行,木条 a 旋转的度数至少是
17、小明晚上6点多外出购物.看手表上时针与分针的夹角为110°,接近7点回到家,发现时针与分针的夹角又是110°,问小明外出时用了 时间
18、如图,三角板的直角顶点落在矩形纸片的一 边上.若∠1=35°,则∠2 的度数是
19、如图,B、C、D依次是线段AE上的三点,已知AE=8.9cm,BD=3cm则图中以A、B、C、D、E这5个点为端点的所有线段长度的和为_______cm.
20、如图,点 D 在△ABC 边 AB 的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D 的度数是
21、将一张长方形纸片按如图所示的方式折叠,EC,ED为折痕,折叠后点A′,B′,E在同一直线上,则∠CED的度数为
22、已知直线 m∥n,将一块含 30°角的直角三角 板 ABC 按如图方式放置(∠ABC=30°),其中 A,B 两点分别落在直线 m,n 上, 若∠1=20°,则∠2 的度数为
三、解答题:
23、如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
24、如图,AB∥CD,点 E 在线段 BC 上,CD=CE.若∠ABC=30°, 则∠D的度数为多少?
25、如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
26、设有甲、乙、丙三人,他们的步行速度相同,骑车速度也相同,骑车的速度为步行速度的3倍,现甲自A地去B地,乙、丙则从B地去A地,双方同时出发,出发时,甲、乙为步行,丙骑车,途中,当甲、丙相遇时,丙将车给甲骑,自己改为步行,三人仍按各自原有方向继续前进;当甲、乙相遇时,甲将车给乙骑,自己又步行,三人仍按各自方向继续前进,问:三人之中谁最选到达自己的目的地?谁最后到达目的地?
27、(1)如图①,已知点A,B位于直线MN的两侧,请在直线MN上找一点P,使PA+PB最小,并说明依据.
(2)如图②,动点O在直线MN上运动,连接AO,分别作∠AOM,∠AON的平分线OC,OD,∠COD的度数是否发生变化?若不变,求出∠COD的度数;若变化,说明理由.
一、选择题:
1、C
2、B
3、C
4、B
5、D
6、B
7、B
8、D
9、B
10、C
11、B
12、C
二、填空题:
13、2/3
14、60°
15、60°
16、20°
17、40分钟
18、55°
19、41.6
20、59°
21、90°
22、50°
三、解答题:
23、(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
24、∵AB∥CD,
∴∠C=∠ABC=30°, 又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即 30°+2∠D=180°,
∴∠D=75°.
25、(1)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∵∠BOC=50°,∠BOA=80°,
∴∠BOD=25°,∠BOE=40°,
∴∠DOE=25°+40°=65°;
(2)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∵∠AOC=150°,
∴∠DOE=∠DOB+∠EOB=(∠BOC+∠BOA)=∠AOC=75°;
(3)∠DOE=∠AOC;
理由是:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=∠BOC,∠BOE=∠COE=∠BOA,
∴∠DOE=∠DOB+∠EOB=(∠BOC+∠BOA)=∠AOC.
26、丙最先到达目的地,甲最后到达目的地.
27、(1)连接AB交MN于点P,则P就是所求的点(图略).依据:两点之间线段最短.
(2)∠COD的度数不会发生变化.
∵OC是∠AOM的平分线,
∴∠COA=∠AOM.
∵OD是∠AON的平分线,
∴∠AOD=∠AON.
∵∠AOM+∠AON=180°,
∴∠COD=∠COA+∠AOD=∠AOM+∠AON=(∠AOM+∠AON)=90°.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
