江苏省徐州市2019届高三12月月考试题数学(小题解析)
文档属性
| 名称 | 江苏省徐州市2019届高三12月月考试题数学(小题解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-13 22:56:23 | ||
图片预览



文档简介
江苏省徐州市2019届高三12月月考试题
数学Ⅰ试卷
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1.设集合,,则= ▲ .
考点:集合的运算,绝对值不等式,二次函数的图象及性质。
答案:
解析:A=,,
所以,=
2.已知,其中为虚数单位,则= ▲ .
考点:复数的运算,复数相等的性质。
答案:2
解析:,
所以,m=-1,n=3,m+n=2
3. 函数的定义域是,则函数的定义域为 ▲ .
考点:函数的定义域,对数函数的性质。
答案:
解析:因为的定义域是,所以,
,所以,
4. 在△ABC中,角A,B,C的对边分别为a,b,c,若a=3,b=5,c=7,则角C= ▲ .
考点:余弦定理。
答案:
解析:由余弦定理,得:cosC=,
所以,C=。
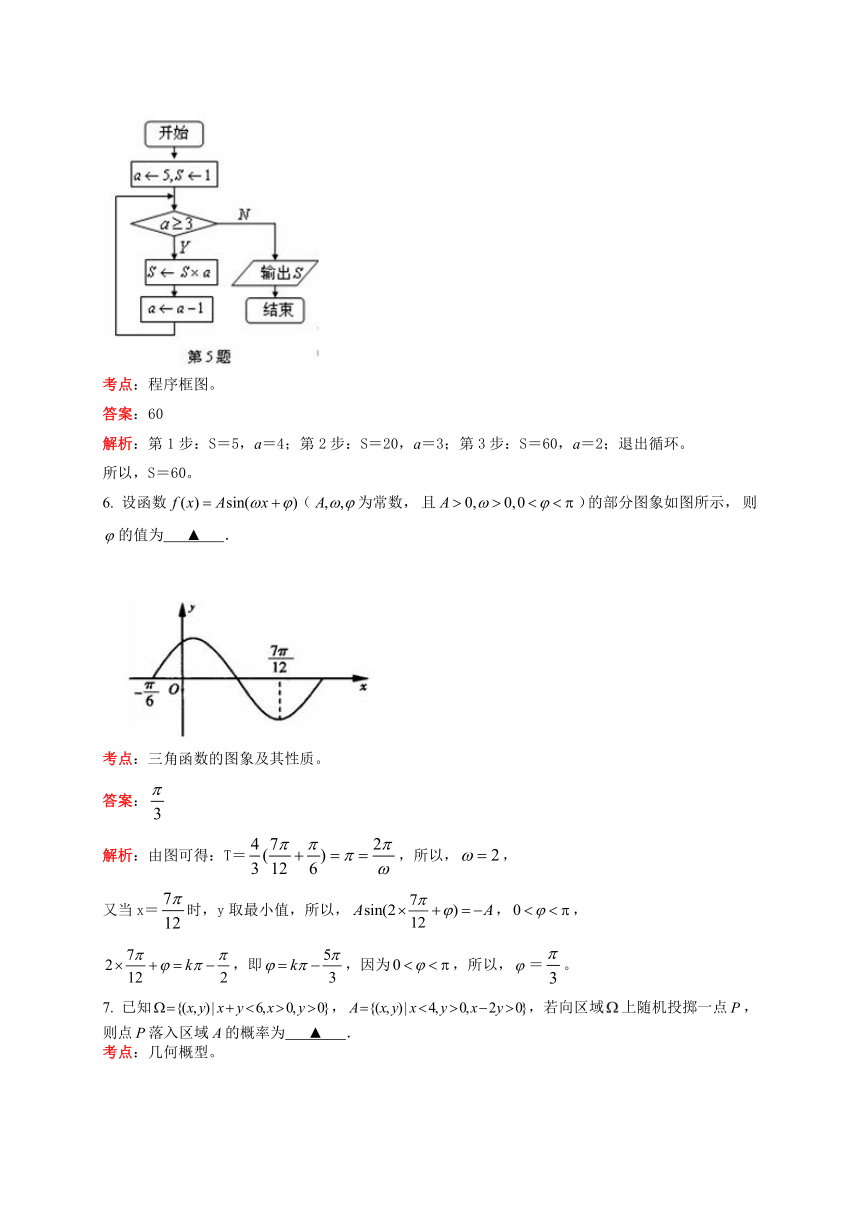
5. 如图,程序执行后输出的结果为 ▲ .
考点:程序框图。
答案:60
解析:第1步:S=5,a=4;第2步:S=20,a=3;第3步:S=60,a=2;退出循环。
所以,S=60。
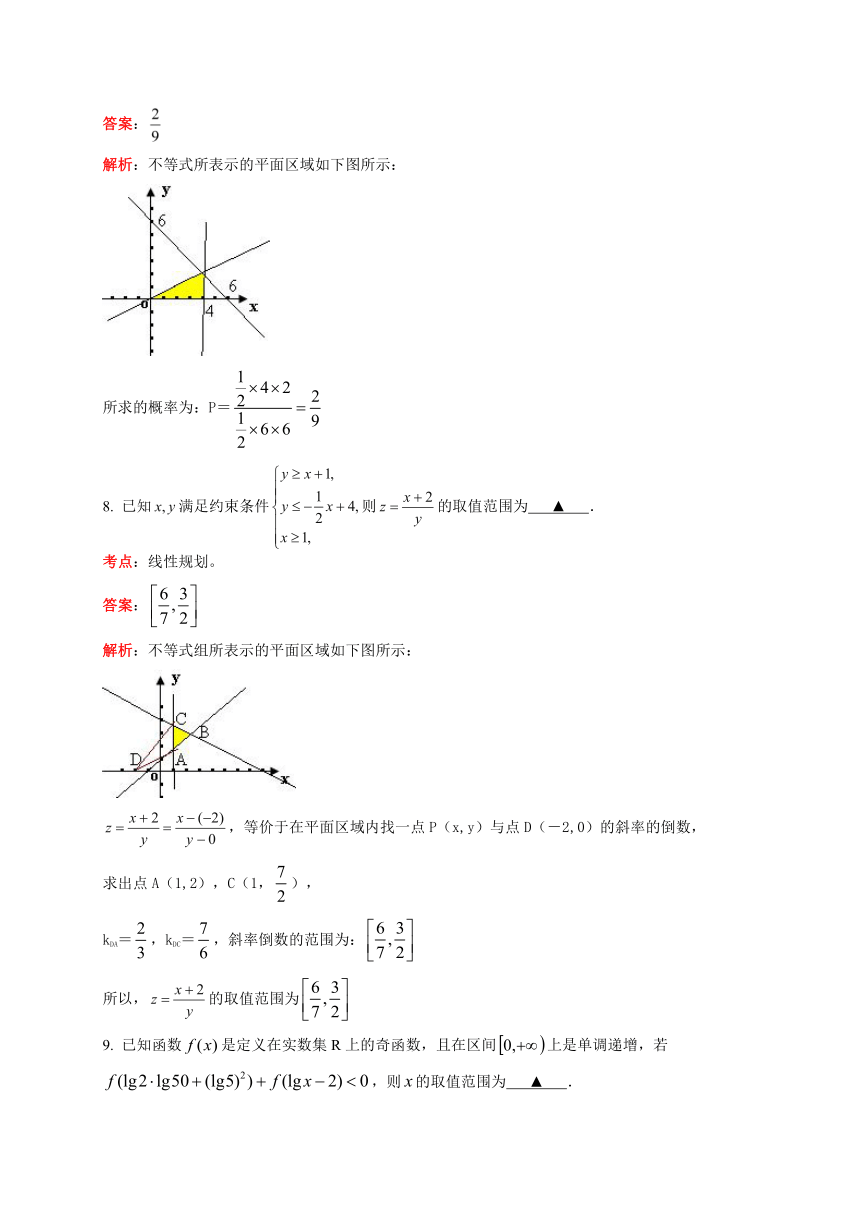
6. 设函数(为常数, 且)的部分图象如图所示, 则的值为 ▲ .
考点:三角函数的图象及其性质。
答案:
解析:由图可得:T=,所以,,
又当x=时,y取最小值,所以,,,
,即,因为,所以,=。
7. 已知,,若向区域上随机投掷一点,则点落入区域的概率为 ▲ .
考点:几何概型。
答案:
解析:不等式所表示的平面区域如下图所示:
所求的概率为:P=
8. 已知满足约束条件则的取值范围为 ▲ .
考点:线性规划。
答案:
解析:不等式组所表示的平面区域如下图所示:
,等价于在平面区域内找一点P(x,y)与点D(-2,0)的斜率的倒数,
求出点A(1,2),C(1,),
kDA=,kDC=,斜率倒数的范围为:
所以,的取值范围为
9. 已知函数是定义在实数集R上的奇函数,且在区间上是单调递增,若
,则的取值范围为 ▲ .
考点:对数运算,函数的奇偶性,单调性。
答案:
解析:=
=1
所以,,化为:
,由函数是奇函数,得:,
∵函数f(x)是定义在实数集R上的奇函数,且在区间[0,+∞)上是单调递增,
∴函数f(x)是在实数集R上单调递增
∴lgx-2<-1,∴lgx<1,∴0<x<10,
故答案为:(0,10)
10. 已知,则 ▲
考点:三角恒等变换,同角三角函数之间的关系。
答案:
解析:,
,所以,,所以,
==。
11. 设数列的前项和为,若,则数列的通项公式为 ▲ .
考点:由数列的前项和为,求的通项公式,等比数列。
答案:
解析:(1)当n=1时,,得:,
(2)当n>1时,,所以,,即
,化为:-1,即2
所以,数列是以-2为首项2为公比的等比数列,
所以,,所以
12. 已知正实数满足,则的最小值为 ▲ .
考点:一元二次不等式,配方法,换元法。
答案:
解析:化为:,
令令m=2(x+y),可化为,
去分母,得:,即:,
化为,
因为m为正数,所以,得:,
即:,所以,,
即的最小值为。
13. 已知函数,如果存在实数,其中,使得,则的取值范围是 ▲ .
考点:对数函数的图象,分段函数图象,函数的导数及其应用。
答案:
解析:画出分段函数图象如下图,
存在实数,其中,使得,
如图可知:-2≤m≤-1,-1<n≤e-2,
且,即:,
所以,,
=0,得:n=0,所以,
n (-1,0) 0 (0,e-2]
- 0 +
↘ ↗
所以,有最小值为:3-ln2,
又2,<2
所以,的值域为
14. 设函数,则满足的的取值范围是 ▲ .
考点:指数函数,函数的奇偶性,导数及其应用,对数函数,基本不等式等。
答案:
解析:函数的定义域为R,
所以,f(x)是R上的奇函数,所以:f(0)=0,
求导:f'(x)=+-2≥2ln3-2>0
所以,f(x)是R上的单调递增函数,
不等式,则有:
,或,
即:,或,
所以,x>2或0<x<1
二.解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤.
15.(本小题满分14分)
如图,在四棱锥中,平面平面,BC//平面PAD,,
.求证:
(1)平面;
(2)平面平面.
16.(本小题满分14分)
在△ABC中,角A,B,C所对边分别为a,b,c,且.
(1)求角A;
(2)若m,n,试求|mn|的最小值.
17.(本小题满分14分)
如图,在平面直角坐标系中,过椭圆:的左顶点作直线,与椭圆和轴正半轴分别交于点,.
(1)若,求直线的斜率;
(2)过原点作直线的平行线,与椭圆交于点,求证:为定值.
18.(本小题满分16分)
如图,某森林公园有一直角梯形区域ABCD,其四条边均为道路,AD∥BC,∠ADC=90°,AB=5千米,BC=8千米,CD=3千米.现甲、乙两管理员同时从地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.
(1)若甲、乙两管理员到达D的时间相差不超过15分钟,求乙的速度v的取值
范围;
(2)已知对讲机有效通话的最大距离是5千米.若乙先到达D,且乙从A到D的过程中始终能用对讲机与甲保持有效通话,求乙的速度v的取值范围.
19.(本小题满分16分)
设数列的前n项和为,数列满足: ,且数列的前n项和为.
(1)求的值;
(2)求证:数列是等比数列;
(3)抽去数列中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列,若的前n项和为,求证:.
20.(本小题满分16分)
已知函数,.
(1)当时,求的单调增区间;
(2)若恰有三个不同的零点().
①求实数的取值范围;
②求证:.
第Ⅱ卷(附加题 共40分)
21.【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分。解答应写出文字说明、证明过程或演算步骤.
A.选修4—1 几何证明选讲
如图,AB为⊙O的直径,BD是⊙O的切线,连接AD交⊙O于E,若BD∥CE,
AB交CE于M,求证:
B.选修4—2 矩阵与变换
已知矩阵,其中,若点在矩阵的变换下得到点.
(1)求实数a的值;
(2)求矩阵的特征值及其对应的特征向量.
C.选修4—4 参数方程与极坐标
已知圆的极坐标方程为,求的最大值.
D.选修4—5 不等式证明选讲
已知均为正数,求证:.
【必做题】第22题、第23题,每题10分,共计20分.
22.(本小题满分10分)
设为整数,集合中的数由小到大组成数列.
(1)写出数列的前三项;
(2)求.
23.(本小题满分10分)
如图,过抛物线上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点
(1) 求的值;
(2) 若,求面积的最大值。
江苏省徐州市2019届高三12月月考试题
数学Ⅰ试卷参考答案
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
二.解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或计算步骤.
15.证明:(1)因为BC//平面PAD,
而BC平面ABCD,平面ABCD平面PAD = AD,
所以BC//AD. …………………………………3分
因为AD 平面PBC,BC平面PBC,
所以平面.………………………………………………6分
(2)自P作PHAB于H,因为平面平面,且平面平面=AB,
所以平面.………………………………………9分
因为BC平面ABCD,所以BCPH.
因为,所以BCPB,
而,于是点H与B不重合,即PB PH = H.
因为PB,PH平面PAB,所以BC平面PAB.…12分
因为BC平面PBC,故平面PBC平面PAB.……………………………… 14分
16.解:(1), ………………………3分
即,
∴,∴. ……………………………5分
∵,∴. ……………………………………7分
(2)mn ,
|mn|.…10分
∵,∴,∴.
从而. …………………………12分
∴当=1,即时,|mn|取得最小值. ………13分
所以,|mn|. …………………………………………14分
17. 解:(1)依题意,椭圆的左顶点,
设直线的斜率为,点的横坐标为,
则直线的方程为.① …………………………… 2分
又椭圆:, ②
由①②得,,
则,从而. ………………………… 5分
因为,所以.
所以,解得(负值已舍). ………………… 8分
(2)设点的横坐标为.结合(1)知,直线的方程为.③
由②③得,. ……………………… 10分
从而 ………………………………… 12分
,即证. ………………………………… 14分
18.解:(1)由题意,可得AD=12千米.
由题可知|-|≤, ··············································2分
解得≤v≤. ······································4分
(2) 解法一:经过t小时,甲、乙之间的距离的平方为f(t).
由于先乙到达D地,故<2,即v>8. ······························6分
①当0<vt≤5,即0<t≤时,
f(t)=(6t)2+(vt)2-2×6t×vt×cos∠DAB=(v2-v+36) t2.
因为v2-v+36>0,所以当t=时,f(t)取最大值,
所以(v2-v+36)×()2≤25,解得v≥. ···································9分
②当5<vt≤13,即<t≤时,
f(t)=(vt-1-6t)2+9=(v-6) 2 (t-)2+9.
因为v>8,所以<,(v-6) 2>0,所以当t=时,f(t)取最大值,
所以(v-6) 2 (-)2+9≤25,解得≤v≤. ···························13分
③当13≤vt≤16, ≤t≤时,
f(t)=(12-6t)2+(16-vt)2,
因为12-6t>0,16-vt>0,所以当f(t)在(,)递减,所以当t=时,f(t)取最大值,
(12-6×)2+(16-v×)2≤25,解得≤v≤.
因为v>8,所以 8<v≤. ······································16分
解法二:设经过t小时,甲、乙之间的距离的平方为f(t).
由于先乙到达D地,故<2,即v>8. ··································6分
以A点为原点,AD为x轴建立直角坐标系,
①当0<vt≤5时,f(t)=(vt-6t)2+(vt)2.
由于(vt-6t)2+(vt)2≤25,所以(v-6)2+(v)2≤对任意0<t≤都成立,
所以(v-6)2+(v)2≤v2,解得v≥. ·······································9分
②当5<vt<13时,f(t)=(vt-1-6t)2+32.
由于(vt-1-6t)2+32≤25,所以-4≤vt-1-6t≤4对任意<t<都成立,
即eq \b\lc\{(\a\al(v-6≤,,-≤v-6,))对任意≤t≤都成立,
所以eq \b\lc\{(\a\al(v-6≤,,-≤v-6,))解得≤v≤. ······································13分
③当13≤vt≤16即≤t≤,此时f (t)=(12-6t)2+(16-vt)2.
由①及②知:8<v≤,于是0<12-6t≤12-≤12-eq \F(78,)=4,
又因为0≤16-vt≤3,所以f (t)=(12-6t)2+(16-vt)2≤42+32=25恒成立.
综上①②③可知8<v≤. ·······································16分
19. (1)由题意得: ;………………1分
当n=1时,则有: 解得: ;
当n=2时,则有: ,即,解得: ;
………………3分
(2) 由 ① 得:
② ………………4分
② - ①得: ,
即: 即:; ……………5分
,由知:
数列是以4为首项,2为公比的等比数列.…………………………………7分
(3)由(2)知: ,即……………………8分
当n≥2时, 对n=1也成立,
即(n………………………………………………………….…10分
数列为,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………11分
当n=2k-1 时,
…………………14分
当n=2k 时,
.……………………………………………………………16分
20.(1)当时,,定义域为.
.
所以,在上单调递增;
即的单调增区间为. …………………………………………3分
(2)①由题意可得,关于的方程在上有三个不同的解.
即关于的方程在上有三个不同的解.
令,.
所以. ………………………5分
显然,当时,,证明如下:
令,.
当时,,函数在上单调递减;
当时,,函数在上单调递增.
所以当时,取最小值.
所以,当时,. ………………………………………7分
令,可得或.
将x,h1(x),h(x)变化情况列表如下
极小值 极大值
又当
所以,实数的取值范围为. ………………………………10分
②由①可知,当时,.
令,则,
即,,. ……………12分
不妨设,则.
又,,
当时,,在上单调递增;
当时,,在上单调递减.
显然,当时,;当时,.
所以,. ……………………………………14分
所以
.
即. ………………………16分
附加题答案
21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.(几何证明选讲,本小题满分10分)
解:连接CB
因为AB为⊙O的直径,BD是⊙O的切线,
所以
因为BD∥CE,所以
因为AB交CE于M,所以M为CE的中点,
所以AC=AE,……………………5分
因为BD是⊙O的切线,所以∠ABD=90°
因为AB为⊙O的直径,所以∠ACB=90°
所以∠ACB=∠ABD
因为,所以△ACB∽△ABD
所以,所以
即……………………10分
B.(矩阵与变换,本小题满分10分)
(1)由=,(2分) ∴. (3分)
(2)由(1)知,则矩阵的特征多项式为
(5分)
令,得矩阵的特征值为与4. (6分)
当时,
∴矩阵的属于特征值的一个特征向量为; (8分)
当时,
∴矩阵的属于特征值的一个特征向量为. (10分)
C.(极坐标与参数方程,本小题满分10分)
原方程化为
即………………………3分
∴圆的直角坐标方程为 ……………5分
圆心M(2 , 2),半径为……………………7分
∴…………………10分
D.(不等式选讲,本小题满分10分)
证明:由柯西不等式得…………………5分
则,
即………………………10分
22.(本题满分10分)
∵为整数且,∴最小取2,此时符合条件的数有;…4分
,可在中取,符合条件有的数有;……5分
同理,时,符合条件有的数有;……6分
时,符合条件有的数有;……7分
时,符合条件有的数有;……8分
时,符合条件有的数有;……9分
因此,是中的最小值,即……10分
23.(本题满分10分)
⑴因为,在抛物线上,
所以, ,
同理,依题有,
因为,所以. ……………………………4分
⑵由⑴知,设的方程为,
到的距离为,,
所以=
, …………………………………………………8分
令,由,,可知.,
因为为偶函数,只考虑的情况,
记,,故在是单调增函数,故的最大值为,故的最大值为6.……………………10分
C
B
A
P
D
H
同课章节目录
