【易错题】冀教版九年级上第25章图形的相似单元检测试卷含解析
文档属性
| 名称 | 【易错题】冀教版九年级上第25章图形的相似单元检测试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 253.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-12 19:45:03 | ||
图片预览


文档简介
【易错题解析】冀教版九年级数学上册 第25章 图形的相似 单元检测试卷
一、单选题(共10题;共30分)
1.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.?15m?????????????????????????????????/B.?60m?????????????????????????????????/C.?20m?????????????????????????????????/D.?10 /m
2.如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ /= /?;④AB2=BD?BC . 其中一定能够判定△ABC是直角三角形的有( ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
3.线段MN长为1cm,点P是MN的黄金分割点,则MP的长是(?? )
A.?
5
?1
2
???????????????????????????/B.?
3?
5
2
???????????????????????????/C.?
5
?1
2
或
3?
5
2
???????????????????????????/D.?不能确定
4.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=
1
2
OD′,则A′B′∶AB为( ??) /
A.?2∶3????????????????????????????????????/B.?3∶2????????????????????????????????????/C.?1∶2????????????????????????????????????/D.?2∶1
5.如图,l1∥l2∥l3 , 其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③
????
????
=
????
????
. 其中正确的有( )
/
A.?3个 B.?2个 ????C.?1个 ?D.?0个
6.如图,小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为(?? ) /
A.?10m??????????????????????????????????????/B.?9m??????????????????????????????????????/C.?8m??????????????????????????????????????/D.?7m
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.?75cm,115cm???????????????/B.?60cm,100cm???????????????/C.?85cm,125cm???????????????/D.?45cm,85cm
8.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM∶MC等于 (???? ) /
A.?1∶2????????????????????????????????????/B.?1∶3????????????????????????????????????/C.?1∶4????????????????????????????????????/D.?1∶5
9.如图,在△??????中,点??、??分别在????、????上,????//????,若????=4,????=2,则
????
????
的值为(???? ) //
A.?
1
2
??????????????????????????????????????????/B.?
2
3
??????????????????????????????????????????/C.?
3
4
??????????????????????????????????????????/D.?2
10.(2017?贵港)如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是
1
2
,其中正确结论的个数是(?? )
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
二、填空题(共10题;共33分)
11.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=10,BD=5,AE=6,则CE的长为________。//
12.在某天的同一时刻,高为 1.5?? 的小明的影长为 1?? ,烟囱的影长为 20?? ,则这座烟囱的高为________ ?? .
13.如图,在△ABC中,DE∥BC,
????
????
=
1
3
,则
????
????
=________. 14.为了测量校园里水平地面上的一棵大树的高度,数学综合实践活动小组的同学们开展如下活动:某一时刻,测得身高1.6m的小明在阳光下的影长是1.2m,在同一时刻测得这棵大树的影长是3.6m,则此树的高度是________m.
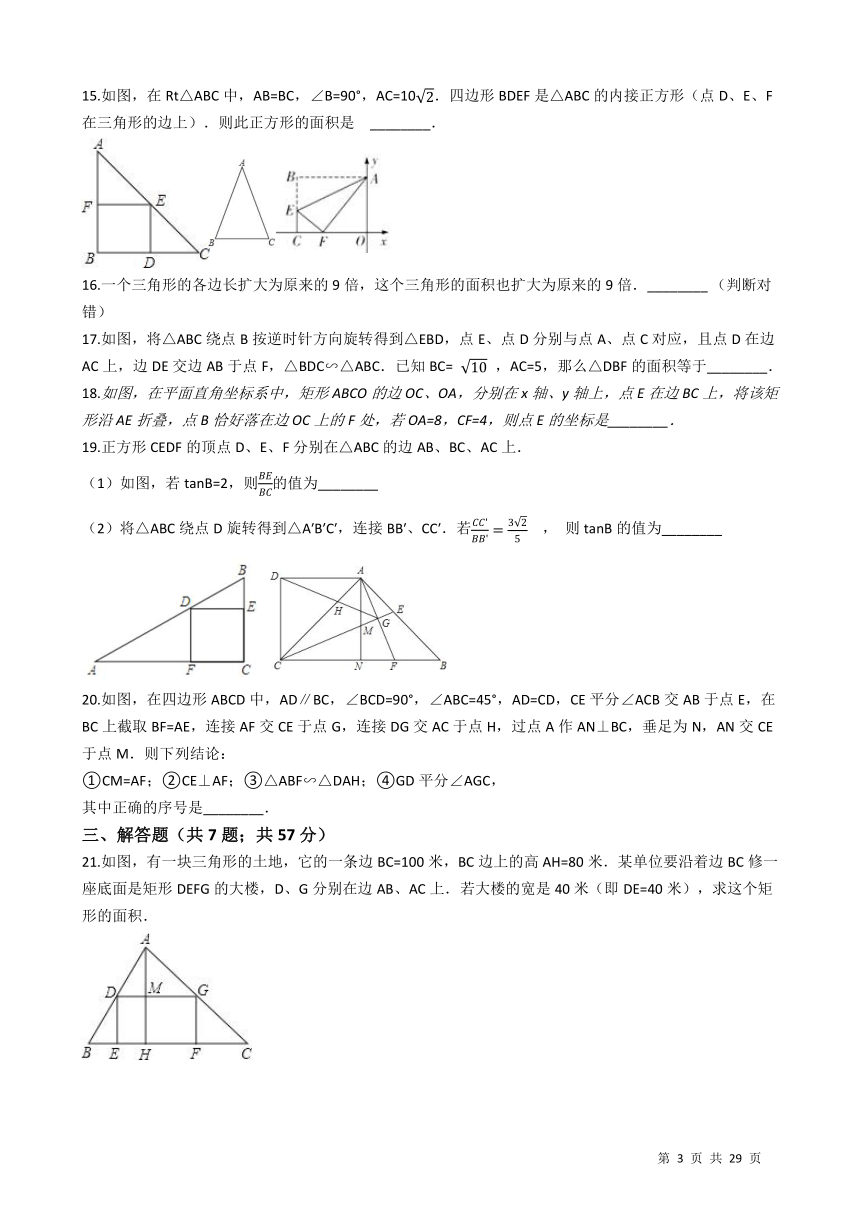
15.如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10
2
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 ________. ///
16.一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.________?(判断对错)
17.如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC=
10
,AC=5,那么△DBF的面积等于________.
18.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. 19.正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. (1)如图,若tanB=2,则
????
????
的值为________? (2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若
????′
????′
=
3
2
5
, 则tanB的值为________? //
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. 三、解答题(共7题;共57分)
21.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积. /?
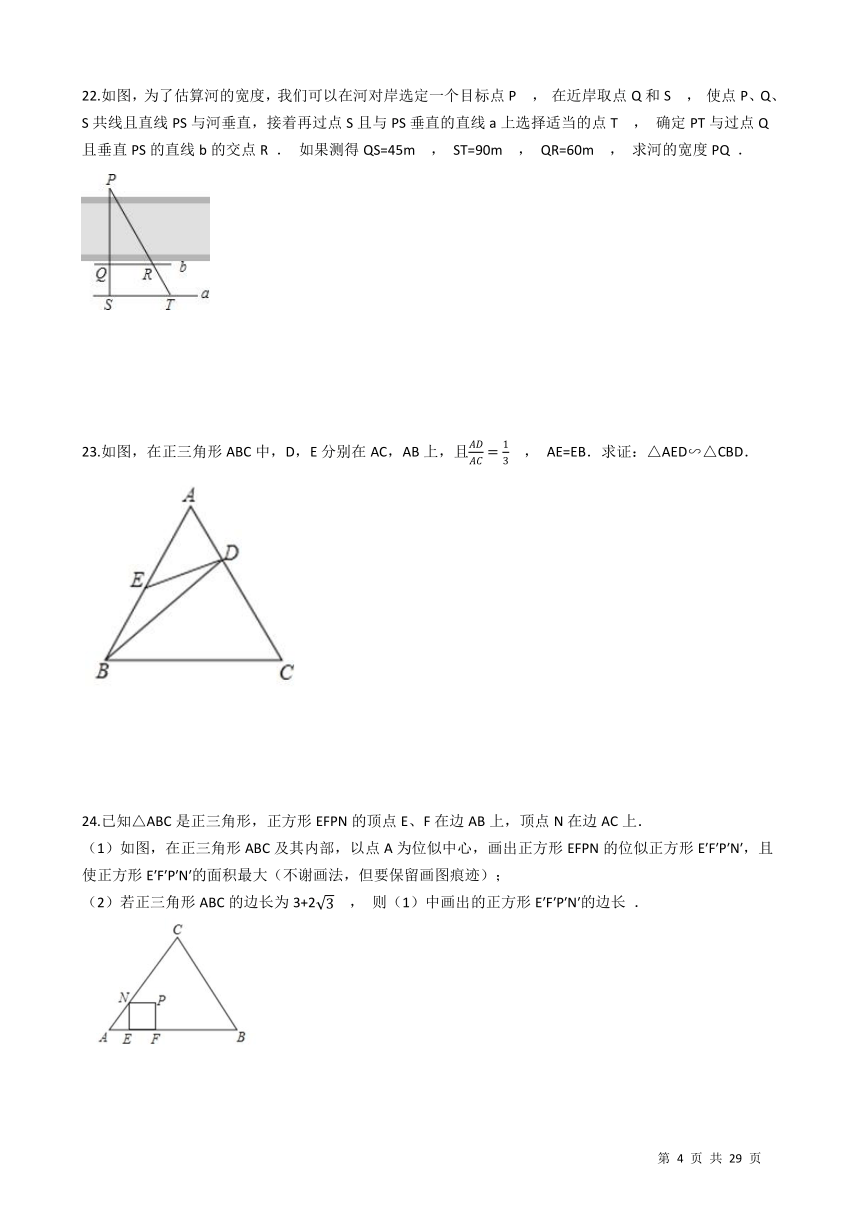
22.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . /?
23.如图,在正三角形ABC中,D,E分别在AC,AB上,且
????
????
=
1
3
, AE=EB.求证:△AED∽△CBD. ?/
24.已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上. (1)如图,在正三角形ABC及其内部,以点A为位似中心,画出正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不谢画法,但要保留画图痕迹); (2)若正三角形ABC的边长为3+2
3
, 则(1)中画出的正方形E′F′P′N′的边长 . ?/
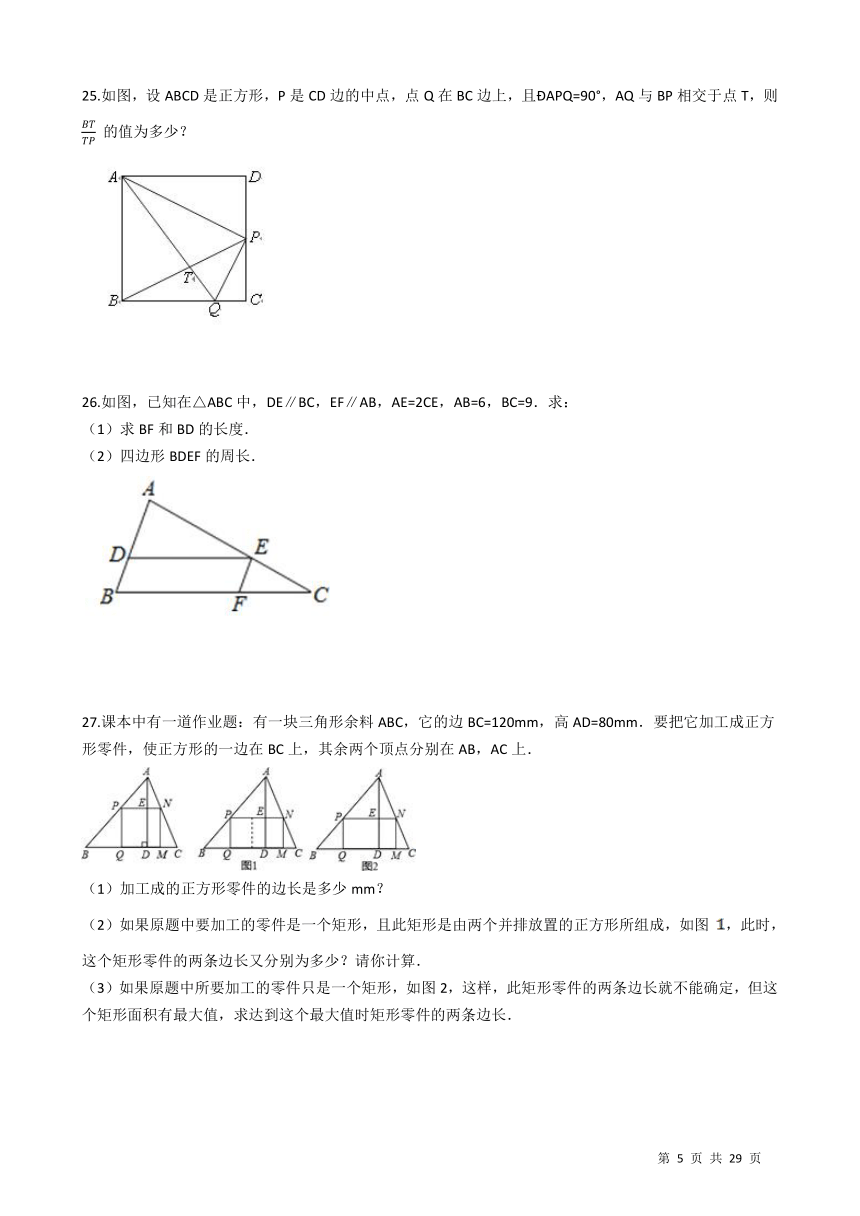
25.如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,且DAPQ=90°,AQ与BP相交于点T,则
????
????
的值为多少? /
26.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
27.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. /
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图 /,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
答案解析部分
一、单选题
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】3
12.【答案】30
13.【答案】
1
3
14.【答案】4.8
15.【答案】25
16.【答案】×
17.【答案】
45
16
18.【答案】(-10,3)
19.【答案】
1
3
;
3
4
20.【答案】①②③④
三、解答题
21.【答案】解答:由已知得,DG∥BC ∴△ADG∽△ABC , ∵AH⊥BC ∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) /= /, 即DG= /=50(m), ∴S矩形DEFG=DE×DG=2000(m2).
22.【答案】解答:根据题意得出:QR∥ST , 则△PQR∽△PST , 故 /= /, ∵QS=45m,ST=90m,QR=60m, ∴ /= /, 解得:PQ=90(m), ∴河的宽度为90米.
23.【答案】证明:∵△ABC为正三角形, ∴∠A=∠C=60°,BC=AB, ∵AE=BE, ∴CB=2AE, ∵
????
????
=
1
3
, ∴CD=2AD, ∴
????
????
=
????
????
=
1
2
, 而∠A=∠C, ∴△AED∽△CBD.
24.【答案】解:(1)如图①,正方形E′F′P′N′即为所求. (2)设正方形E′F′P′N′的边长为x, ∵△ABC为正三角形, ∴AE′=BF′=
3
3
x. ∵E′F′+AE′+BF′=AB, ∴x+
3
3
x+
3
3
x=3+2
3
, ∴解得:x=3, 故答案为:3. ?/
25.【答案】解:
6
5
26.【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
27.【答案】(1)解:如图1, / 设正方形的边长为xmm,则PN=PQ=ED=x, ∴AE=AD-ED=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
??
120
=
80???
80
, 解得x=48. ∴加工成的正方形零件的边长是48mm (2)解:如图2, / 设PQ=x,则PN=2x,AE=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
2??
120
=
80???
80
, 解得: ??=
240
7
, ∴ 2??=
480
7
, ∴这个矩形零件的两条边长分别为
240
7
mm,
480
7
mm (3)解:如图3, / 设PN=x(mm),矩形PQMN的面积为S (??
??
2
) , 由条件可得 △??????~△?????? , ∴
????
????
=
????
????
, 即
??
120
=
80?????
80
, 解得: ????=80?
2
3
?? . 则 ??=?????????=??(80?
2
3
??)=?
2
3
??
2
+80??=?
2
3
(???60)
2
+2400 , 故S的最大值为 2400??
??
2
,此时 ????=60???? , ????=80?
2
3
×60=40(????)
【易错题解析】冀教版九年级数学上册 第25章 图形的相似 单元检测试卷
一、单选题(共10题;共30分)
1.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.?15m?????????????????????????????????/B.?60m?????????????????????????????????/C.?20m?????????????????????????????????/D.?10 /m
【答案】A
【考点】相似三角形的应用
【解析】【解答】设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得: /= /, ∴x= /=15 ∴这棵树的高度是15m. 故选A. 【分析】在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
2.如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ /= /?;④AB2=BD?BC . 其中一定能够判定△ABC是直角三角形的有( ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
【答案】B
【考点】相似三角形的判定与性质
【解析】解答:(1)∠B+∠DAC=90°,该条件无法判定△ABC是直角三角形;(2)∵∠B=∠DAC , ∠BAD+∠B=90°,∴∠BAD+∠DAC=90°,即∠BAC=90°,故该条件可以判定△ABC是直角三角形;(3) /= /,该条件无法判定△ABC是直角三角形;(4)∵AB2=BD?BC , ∴ /= /, ∵∠B=∠B , ∴△ABD∽△CBA , ∴∠BAC=90°,故该条件可以判定△ABC是直角三角形; 故选 B 分析:对题干中给出的条件逐一验证,证明∠BAC=90°即可解题.
3.线段MN长为1cm,点P是MN的黄金分割点,则MP的长是(?? )
A.?
5
?1
2
???????????????????????????/B.?
3?
5
2
???????????????????????????/C.?
5
?1
2
或
3?
5
2
???????????????????????????/D.?不能确定
【答案】C
【考点】黄金分割
【解析】【解答】解:设MP=x,则PN=1﹣x,根据题意得
??
1???
=
1???
1
, 解得,x=
3?
5
2
或
3+
5
2
>1(不合题意,舍去), 又因为题中没强调MP是长的一段还是短的一段,所以MP的长也可以为1﹣
3?
5
2
=
5
?1
2
. 故选C. 【分析】根据黄金分割点的概念,结合题目要求,列出方程求解即可.
4.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=
1
2
OD′,则A′B′∶AB为( ??) /
A.?2∶3????????????????????????????????????/B.?3∶2????????????????????????????????????/C.?1∶2????????????????????????????????????/D.?2∶1
【答案】D
【考点】位似变换
【解析】【解答】解:位似图形上任意一对对应点,到位似中心的距离之比都等于相似比. ∴A′B′:AB=OD′:OD=2:1. 故答案为:D. 【分析】由题,根据OD与OD′的数量关系,可以得出两个图形的位似比。
5.如图,l1∥l2∥l3 , 其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③
????
????
=
????
????
. 其中正确的有( )
/
A.?3个
???????????????????????????????????????B.?2个
???????????????????????????????????????C.?1个
???????????????????????????????????????D.?0个
【答案】A
【考点】相似三角形的判定与性质
【解析】【解答】解:l1与l2、l2与l3间的距离为l,则△ADE和△ABC分别是l,2l,
∵l1∥l2∥l3 ,
∴△ADE∽△ABC,
∴故选项②正确.
∵△ADE∽△ABC,
∴
????
????
=
????
????
,
∴故选项③正确,
∵△ADE∽△ABC,
????
????
=
1
21
=
1
2
,
即BC=2DE,
故正确的有3个,
故选:A.
【分析】根据l1∥l2∥l3判断△ADE∽△ABC,根据相似三角形的性质对所给命题进行判断.
6.如图,小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为(?? ) /
A.?10m??????????????????????????????????????/B.?9m??????????????????????????????????????/C.?8m??????????????????????????????????????/D.?7m
【答案】B
【考点】相似三角形的应用
【解析】【解答】解:因为竹竿和旗杆均垂直于地面,所以构成两个相似三角形, 若设旗杆高x米, 则
2.4
??
=
8
8+22
, ∴x=9. 故选B. 【分析】利用相似三角形对应边成比例解题.
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.?75cm,115cm???????????????/B.?60cm,100cm???????????????/C.?85cm,125cm???????????????/D.?45cm,85cm
【答案】A
【考点】相似三角形的性质
【解析】【解答】解:根据题意两个三角形的相似比是15:23,周长比就是15:23, 大小周长相差8份,所以每份的周长是40÷8=5cm, 所以两个三角形的周长分别为5×15=75cm,5×23=115cm.故选A. 【分析】根据题意两个三角形的相似比是15:23,可得周长比为15:23,计算出周长相差8份及每份的长,可得两三角形周长.
8.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM∶MC等于 (???? ) /
A.?1∶2????????????????????????????????????/B.?1∶3????????????????????????????????????/C.?1∶4????????????????????????????????????/D.?1∶5
【答案】B
【考点】三角形中位线定理,相似三角形的判定与性质
【解析】【分析】根据中位线定理证明△NDM∽△NBC后求解.
【解答】∵DE是△ABC的中位线,M是DE的中点, ∴DM∥BC,DM=ME=
1
4
BC. ∴△NDM∽△NBC,
????
????
=
????
????
=
1
4
. ∴
????
????
=
1
3
.
故选:B
【点评】本题考查了三角形中位线定理及相似三角形的性质.
9.如图,在△??????中,点??、??分别在????、????上,????//????,若????=4,????=2,则
????
????
的值为(???? ) /
A.?
1
2
??????????????????????????????????????????/B.?
2
3
??????????????????????????????????????????/C.?
3
4
??????????????????????????????????????????/D.?2
【答案】B
【考点】相似三角形的判定与性质
【解析】【分析】由????//????可证得△??????~△??????,再根据相似三角形的性质求解即可。 【解答】∵????//???? ∴△??????~△?????? ∵????=4,????=2 ∴
????
????
=
????
????
=
4
6
=
2
3
故选B。 【点评】相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握。
10.(2017?贵港)如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是
1
2
,其中正确结论的个数是(?? ) /
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
【答案】D
【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
【解析】【解答】解:∵正方形ABCD中,CD=BC,∠BCD=90°, ∴∠BCN+∠DCN=90°, 又∵CN⊥DM, ∴∠CDM+∠DCN=90°, ∴∠BCN=∠CDM, 又∵∠CBN=∠DCM=90°, ∴△CNB≌△DMC(ASA),故①正确; 根据△CNB≌△DMC,可得CM=BN, 又∵∠OCM=∠OBN=45°,OC=OB, ∴△OCM≌△OBN(SAS), ∴OM=ON,∠COM=∠BON, ∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON, 又∵DO=CO, ∴△CON≌△DOM(SAS),故②正确; ∵∠BON+∠BOM=∠COM+∠BOM=90°, ∴∠MON=90°,即△MON是等腰直角三角形, 又∵△AOD是等腰直角三角形, ∴△OMN∽△OAD,故③正确; ∵AB=BC,CM=BN, ∴BM=AN, 又∵Rt△BMN中,BM2+BN2=MN2 , ∴AN2+CM2=MN2 , 故④正确; ∵△OCM≌△OBN, ∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1, ∴当△MNB的面积最大时,△MNO的面积最小, 设BN=x=CM,则BM=2﹣x, ∴△MNB的面积=
1
2
x(2﹣x)=﹣
1
2
x2+x, ∴当x=1时,△MNB的面积有最大值
1
2
, 此时S△OMN的最小值是1﹣
1
2
=
1
2
,故⑤正确; 综上所述,正确结论的个数是5个, 故选:D. / 【分析】根据正方形的性质,依次判定△CNB≌△DMC,△OCM≌△OBN,△CON≌△DOM,△OMN∽△OAD,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
二、填空题(共10题;共33分)
11.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=10,BD=5,AE=6,则CE的长为________。/
【答案】3
【考点】平行线分线段成比例
【解析】【解答】根据平行线分线段成比例定理即由DE∥BC,可直接得
????
????
=
????
????
,即
10
5
=
6
????
,解得EC=3.【分析】运用平分线分线段成比例,列出比例等式求CE的长即可。
12.在某天的同一时刻,高为 1.5?? 的小明的影长为 1?? ,烟囱的影长为 20?? ,则这座烟囱的高为________ ?? .
【答案】30
【考点】平行线分线段成比例
【解析】【解答】解: 设烟囱的高为x, 由题意得:
1.5
1
=
??
20
,
∴x=30
∴烟囱的高为30米.
故答案为:30.
【分析】根据同一时刻,同一地点同一水平面上,不同物体的高度与影长成比例,即可列出方程,求解即可。
13.如图,在△ABC中,DE∥BC,
????
????
=
1
3
,则
????
????
=________. /
【答案】
1
3
【考点】相似三角形的判定与性质
【解析】【解答】解:∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C, ∴△ADE∽△ABC, ∴
????
????
=
????
????
=
1
3
. 故答案为:
1
3
【分析】根据相似三角形的对应边成比例求解。
14.为了测量校园里水平地面上的一棵大树的高度,数学综合实践活动小组的同学们开展如下活动:某一时刻,测得身高1.6m的小明在阳光下的影长是1.2m,在同一时刻测得这棵大树的影长是3.6m,则此树的高度是________m.
【答案】4.8
【考点】相似三角形的应用,平行投影
【解析】【解答】解:设此树的高度是hm,则
1.6
1.2
=
?
3.6
,解得h=4.8(m). 故答案为:4.8. 【分析】设此树的高度是hm,再根据同一时刻物高与影长成正比即可得出结论.
15.(2015?佛山市)如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10
2
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 ________. /
【答案】25
【考点】正方形的性质,相似三角形的判定与性质
【解析】【解答】∵在Rt△ABC中,AB2+BC2=AC2 , ∵AB=BC,AC=10
2
. ∴2AB2=200, ∴AB=BC=10, 设EF=x,则AF=10﹣x ∵EF∥BC, ∴△AFE∽△ABC ∴
????
????
=
????
????
,即
x
10
=
10???
10
, ∴x=5, ∴EF=5, ∴此正方形的面积为5×5=25. 故答案为25. 【点评】主要考查了正方形基本性质和比例线段的运用.解题的关键是准确的找到相似三角形并根据其相似比列方程求解.
16.一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.________?(判断对错)
【答案】×
【考点】相似三角形的性质
【解析】【解答】解:∵相似三角形的边长的比等于相似比,面积的比等于相似比的平方, ∴一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍,错误. 故答案为:×. 【分析】根据相似多边形的面积的比等于相似比的平方解答.
17.如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC=
10
,AC=5,那么△DBF的面积等于________. /
【答案】
45
16
【考点】相似三角形的性质,旋转的性质
【解析】【解答】解:∵△BDC∽△ABC, ∴
????
????
=
????
????
,∠CBD=∠A, ∴CD=
??
??
2
????
, ∵BC=
10
,AC=5, ∴CD=2, ∴AD=3, ∵将△ABC绕点B按逆时针方向旋转得到△EBD, / ∴∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC, ∴∠EBF=∠CBD, ∴∠EBF=∠A, ∴BE∥AC, ∴∠ADF=∠E, ∴∠E=∠EBF=∠A=∠ADF, ∴EF=BF,AF=DF, ∴AF+BF=EF+DF, 即AB=DE=AC=5, ∵AD∥BE, ∴△ADF∽△BEF, ∴
????
????
=
????
????
=
3
5
, ∴
????
????
=
3
8
, 过A 作AH⊥BC于H, ∴AH=
5
2
?
(
10
2
)
2
=
3
10
2
, ∵S△BDE=S△ABC=
1
2
×
10
×
3
10
2
=
15
2
, ∴△DBF的面积=
3
8
S△ABC=
45
16
. 故答案为:
45
16
. 【分析】根据相似三角形的性质得到
????
????
=
????
????
,∠CBD=∠A,得到CD=2,AD=3,根据旋转的性质得到∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,得到∠EBF=∠A,根据平行线的判定和性质得到∠ADF=∠E,等量代换得到∠E=∠EBF=∠A=∠ADF,根据等腰三角形的判定得到EF=BF,AF=DF,得到AB=DE=AC=5,根据相似三角形的性质得到
????
????
=
3
8
,过A 作AH⊥BC于H,于是得到结论.
18.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. /
【答案】(-10,3)
【考点】勾股定理,矩形的性质,翻折变换(折叠问题),相似三角形的判定与性质
【解析】【解答】解:∵矩形ABCO中, ∴CE∥AO. ∴△CEF∽△OFA. ∴
????
????
=
????
????
. 又∵OA=8,CF=4. ∴OF=2CE. 设CE=x,则BE=8-x. 根据折叠的性质,可得EF=8-x. ∴
??
2
+
4
2
=
(8???)
2
, ∴x=3, ∴OF=6, ∴OC=10, ∴点E的坐标为(-10,3). 故答案为:(-10,3) 【分析】根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得 x 2 + 4 2 = ( 8 ? x ) 2 ,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).
19.正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. (1)如图,若tanB=2,则
????
????
的值为________? (2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若
????′
????′
=
3
2
5
, 则tanB的值为________? /
【答案】
1
3
;
3
4
【考点】相似三角形的判定与性质
【解析】解:(1)∵四边形CEDF为正方形, ∴ED=EC,∠CED=90°, 在Rt△BDE中,∵tanB=
????
????
=2, ∴DE=2BE, ∴/ (2)连结DC、DC′,如图, ∵△ABC绕点D旋转得到△A′B′C′, ∴DB=DB′,DC=DC′,∠BDB′=∠CDC′, 即/ ∴△DBB′∽△DCC′, ∴
????
????
=
????′
????′
=
3
2
5
设DC=3
2
x,BD=5x, ∵四边形CEDF为正方形, ∴DE=3x, 在Rt△BDE中,BE=/ ∴tanB=/ 故答案为
1
3
,
3
4
. / 【分析】(1)由正方形的性质得ED=EC,∠CED=90°,再在Rt△BDE中,利用正切的定义得到DE=2BE,则CE=BE,所以
????
????
=
1
3
; ???????????? (2)连结DC、DC′,如图,根据旋转的性质得DB=DB′,DC=DC′,∠BDB′=∠CDC′,则可判断△DBB′∽△DCC′,根据相似三角形的性质得
????
????
=
????′
????′
=
3
2
5
, 则可设DC=3
2
x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. /
【答案】①②③④
【考点】全等三角形的判定与性质,相似三角形的判定与性质
【解析】【解答】解: / ⑴结论①正确.理由如下: ∵∠1=∠2,∠1+∠CMN=90°,∠2+∠6=90°, ∴∠6=∠CMN,又∵∠5=∠CMN, ∴∠5=∠6, ∴AM=AE=BF. 易知ADCN为正方形,△ABC为等腰直角三角形,∴AB=AC. 在△ACM与△ABF中, {
????=????
∠??????=∠??=45°
????=????
, ∴△ACM≌△ABF(SAS), ∴CM=AF; ⑵结论②正确.理由如下: ∵△ACM≌△ABF,???????????????????????????????? ∴∠2=∠4, ∵∠2+∠6=90°, ∴∠4+∠6=90°, ∴CE⊥AF; ⑶结论③正确.理由如下: 证法一:∵CE⊥AF, ∴∠ADC+∠AGC=180°, ∴A、D、C、G四点共圆, ∴∠7=∠2, ∵∠2=∠4, ∴∠7=∠4, 又∵∠DAH=∠B=45°, ∴△ABF∽△DAH; 证法二:∵CE⊥AF,∠1=∠2, ∴△ACF为等腰三角形,AC=CF,点G为AF中点. 在Rt△ANF中,点G为斜边AF中点, ∴NG=AG, ∴∠MNG=∠3, ∴∠DAG=∠CNG. 在△ADG与△NCG中, {
????=????
∠??????=∠??????
????=????
, ∴△ADG≌△NCG(SAS), ∴∠7=∠1, 又∵∠1=∠2=∠4, ∴∠7=∠4, 又∵∠DAH=∠B=45°, ∴△ABF∽△DAH; ⑷结论④正确.理由如下: 证法一:∵A、D、C、G四点共圆, ∴∠DGC=∠DAC=45°,∠DGA=∠DCA=45°, ∴∠DGC=∠DGA,即GD平分∠AGC. 证法二:∵AM=AE,CE⊥AF, ∴∠3=∠4,又∠2=∠4,∴∠3=∠2 则∠CGN=180°﹣∠1﹣90°﹣∠MNG=180°﹣∠1﹣90°﹣∠3=90°﹣∠1﹣∠2=45°. ∵△ADG≌△NCG, ∴∠DGA=∠CGN=45°=
1
2
∠AGC, ∴GD平分∠AGC. 综上所述,正确的结论是:①②③④,共4个. 故答案为:①②③④ 【分析】 结论①正确,证明△ACM≌△ABF即可;结论②正确,由△ACM≌△ABF得出∠2=∠4,进而得∠4+∠6=90°,即CE⊥AF,结论③正确,证法一:利用四点共圆;证法二:利用三角形全等;结论④正确,证法一:利用四点共圆,证法二:利用三角形全等。
三、解答题(共7题;共57分)
21.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积. /?
【答案】解答:由已知得,DG∥BC ∴△ADG∽△ABC , ∵AH⊥BC ∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) /= /, 即DG= /=50(m), ∴S矩形DEFG=DE×DG=2000(m2).
【考点】相似三角形的应用
【解析】【分析】由于四边形DEFG是矩形,即DG∥EF , 此时有∠ADG=∠B , ∠AGD=∠C , 所以△ADG∽△ABC , 利用相似三角形的性质求得线段DG的长,最后求得矩形的面积.
22.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . /?
【答案】解答:根据题意得出:QR∥ST , 则△PQR∽△PST , 故 /= /, ∵QS=45m,ST=90m,QR=60m, ∴ /= /, 解得:PQ=90(m), ∴河的宽度为90米.
【考点】相似三角形的应用
【解析】【分析】根据相似三角形的性质得出 /= /,进而代入求出即可.
23.如图,在正三角形ABC中,D,E分别在AC,AB上,且
????
????
=
1
3
, AE=EB.求证:△AED∽△CBD. ?/
【答案】证明:∵△ABC为正三角形, ∴∠A=∠C=60°,BC=AB, ∵AE=BE, ∴CB=2AE, ∵
????
????
=
1
3
, ∴CD=2AD, ∴
????
????
=
????
????
=
1
2
, 而∠A=∠C, ∴△AED∽△CBD.
【考点】相似三角形的判定
【解析】【分析】先根据等边三角形的性质得到∠A=∠C=60°,BC=AB,由AE=BE可得到CB=2AE,再由
????
????
=
1
3
得到CD=2AD,则
????
????
=
????
????
, 然后根据两边及其夹角法可得到结论.
24.已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上. (1)如图,在正三角形ABC及其内部,以点A为位似中心,画出正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不谢画法,但要保留画图痕迹); (2)若正三角形ABC的边长为3+2
3
, 则(1)中画出的正方形E′F′P′N′的边长 . ?/
【答案】解:(1)如图①,正方形E′F′P′N′即为所求. (2)设正方形E′F′P′N′的边长为x, ∵△ABC为正三角形, ∴AE′=BF′=
3
3
x. ∵E′F′+AE′+BF′=AB, ∴x+
3
3
x+
3
3
x=3+2
3
, ∴解得:x=3, 故答案为:3. ?/
【考点】位似变换
【解析】【分析】(1)利用位似图形的性质,作出正方形EFPN的位似正方形E′F′P′N′,如答图①所示; (2)根据正三角形、正方形、直角三角形相关线段之间的关系,利用等式E′F′+AE′+BF′=AB,列方程求得正方形E′F′P′N′的边长.
25.如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,且DAPQ=90°,AQ与BP相交于点T,则
????
????
的值为多少? /
【答案】解:
6
5
【考点】平行线的判定,勾股定理,正方形的性质,相似三角形的判定与性质
【解析】【解答】解 : 过点B作BE⊥AQ于点E,过点 P作PH⊥AQ于点H,?? / 设正方形的边长是2.则DP=CP=1,AD=2. ∴AP=
5
∵∠APQ=90°, ∴∠APD+∠CPQ=90° , 又∵∠APD+∠PAD=90° , ∴∠PAD=∠CPQ, ∵∠C=∠D ; ∴△ADP∽△PCQ. ∴AD:PC=AP:PQ=DP:CQ. 即2:1=
5
:PQ=1:CQ, 所以PQ=
5
2
, CQ=0.5. BQ=2?0.5=1.5. ∴AQ=
5
2
S△ABQ=
1
2
AB×BQ=
1
2
AQ×BE BE=
????·????
????
=
6
5
S△APQ=
1
2
AP×PQ=
1
2
AQ×PH, PH=
????·????
????
=1; 又BE⊥AQ,PH⊥AQ, ∴BE∥PH; ∴△BET∽△PHT, BT:PT=BE:PH=6:5. 【分析】 过点B作BE⊥AQ于点E,过点 P作PH⊥AQ于点H, 设正方形的边长是2.则DP=CP=1,AD=2.根据勾股定理得出AQ的长度,根据平角的定义,及直角三角形两锐角互余得出∠APD+∠CPQ=90°,∠APD+∠PAD=90°,根据同角的余角相等得出∠PAD=∠CPQ,从而判断出△ADP∽△PCQ.根据相似三角形对应边成比例得出AD:PC=AP:PQ=DP:CQ.从而得出PQ.CQ,BQ,AQ,的长度,根据面积法得出BE,PH的长度,根据垂直于同一直线的两条直线互相平行得出BE∥PH;根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似,得出△BET∽△PHT,根据相似三角形对应边的比等于对应高的比得出结论。
26.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
【考点】平行线分线段成比例
【解析】【分析】(1)由平行线分线段成比例得出比例式,即可得出结果; (2)先证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
27.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. /
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图 /,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
【答案】(1)解:如图1, / 设正方形的边长为xmm,则PN=PQ=ED=x, ∴AE=AD-ED=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
??
120
=
80???
80
, 解得x=48. ∴加工成的正方形零件的边长是48mm (2)解:如图2, / 设PQ=x,则PN=2x,AE=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
2??
120
=
80???
80
, 解得: ??=
240
7
, ∴ 2??=
480
7
, ∴这个矩形零件的两条边长分别为
240
7
mm,
480
7
mm (3)解:如图3, / 设PN=x(mm),矩形PQMN的面积为S (??
??
2
) , 由条件可得 △??????~△?????? , ∴
????
????
=
????
????
, 即
??
120
=
80?????
80
, 解得: ????=80?
2
3
?? . 则 ??=?????????=??(80?
2
3
??)=?
2
3
??
2
+80??=?
2
3
(???60)
2
+2400 , 故S的最大值为 2400??
??
2
,此时 ????=60???? , ????=80?
2
3
×60=40(????)
【考点】相似三角形的判定与性质,配方法的应用
【解析】【分析】(1)设正方形的边长为x,则PN=PQ=ED=x,AE=AD-ED=80-x,由△APN ~ △ABC,根据相似三角形的性质可得
????
????
=
????
????
,代入可得x。 (2) 设PQ=x,则PN=2x,AE=80-x,由△APN~△ABC,根据相似三角形性质可得,
????
????
=
????
????
, 代入求得PQ,再求得PN。 (3) 根据相似三角形的性质可得
????
????
=
????
????
, 用含有x的代数式表示PQ,再表示面积S,最后配方求得S的最大值。
一、单选题(共10题;共30分)
1.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.?15m?????????????????????????????????/B.?60m?????????????????????????????????/C.?20m?????????????????????????????????/D.?10 /m
2.如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ /= /?;④AB2=BD?BC . 其中一定能够判定△ABC是直角三角形的有( ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
3.线段MN长为1cm,点P是MN的黄金分割点,则MP的长是(?? )
A.?
5
?1
2
???????????????????????????/B.?
3?
5
2
???????????????????????????/C.?
5
?1
2
或
3?
5
2
???????????????????????????/D.?不能确定
4.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=
1
2
OD′,则A′B′∶AB为( ??) /
A.?2∶3????????????????????????????????????/B.?3∶2????????????????????????????????????/C.?1∶2????????????????????????????????????/D.?2∶1
5.如图,l1∥l2∥l3 , 其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③
????
????
=
????
????
. 其中正确的有( )
/
A.?3个 B.?2个 ????C.?1个 ?D.?0个
6.如图,小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为(?? ) /
A.?10m??????????????????????????????????????/B.?9m??????????????????????????????????????/C.?8m??????????????????????????????????????/D.?7m
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.?75cm,115cm???????????????/B.?60cm,100cm???????????????/C.?85cm,125cm???????????????/D.?45cm,85cm
8.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM∶MC等于 (???? ) /
A.?1∶2????????????????????????????????????/B.?1∶3????????????????????????????????????/C.?1∶4????????????????????????????????????/D.?1∶5
9.如图,在△??????中,点??、??分别在????、????上,????//????,若????=4,????=2,则
????
????
的值为(???? ) //
A.?
1
2
??????????????????????????????????????????/B.?
2
3
??????????????????????????????????????????/C.?
3
4
??????????????????????????????????????????/D.?2
10.(2017?贵港)如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是
1
2
,其中正确结论的个数是(?? )
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
二、填空题(共10题;共33分)
11.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=10,BD=5,AE=6,则CE的长为________。//
12.在某天的同一时刻,高为 1.5?? 的小明的影长为 1?? ,烟囱的影长为 20?? ,则这座烟囱的高为________ ?? .
13.如图,在△ABC中,DE∥BC,
????
????
=
1
3
,则
????
????
=________. 14.为了测量校园里水平地面上的一棵大树的高度,数学综合实践活动小组的同学们开展如下活动:某一时刻,测得身高1.6m的小明在阳光下的影长是1.2m,在同一时刻测得这棵大树的影长是3.6m,则此树的高度是________m.
15.如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10
2
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 ________. ///
16.一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.________?(判断对错)
17.如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC=
10
,AC=5,那么△DBF的面积等于________.
18.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. 19.正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. (1)如图,若tanB=2,则
????
????
的值为________? (2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若
????′
????′
=
3
2
5
, 则tanB的值为________? //
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. 三、解答题(共7题;共57分)
21.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积. /?
22.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . /?
23.如图,在正三角形ABC中,D,E分别在AC,AB上,且
????
????
=
1
3
, AE=EB.求证:△AED∽△CBD. ?/
24.已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上. (1)如图,在正三角形ABC及其内部,以点A为位似中心,画出正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不谢画法,但要保留画图痕迹); (2)若正三角形ABC的边长为3+2
3
, 则(1)中画出的正方形E′F′P′N′的边长 . ?/
25.如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,且DAPQ=90°,AQ与BP相交于点T,则
????
????
的值为多少? /
26.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
27.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. /
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图 /,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
答案解析部分
一、单选题
1.【答案】A
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】D
二、填空题
11.【答案】3
12.【答案】30
13.【答案】
1
3
14.【答案】4.8
15.【答案】25
16.【答案】×
17.【答案】
45
16
18.【答案】(-10,3)
19.【答案】
1
3
;
3
4
20.【答案】①②③④
三、解答题
21.【答案】解答:由已知得,DG∥BC ∴△ADG∽△ABC , ∵AH⊥BC ∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) /= /, 即DG= /=50(m), ∴S矩形DEFG=DE×DG=2000(m2).
22.【答案】解答:根据题意得出:QR∥ST , 则△PQR∽△PST , 故 /= /, ∵QS=45m,ST=90m,QR=60m, ∴ /= /, 解得:PQ=90(m), ∴河的宽度为90米.
23.【答案】证明:∵△ABC为正三角形, ∴∠A=∠C=60°,BC=AB, ∵AE=BE, ∴CB=2AE, ∵
????
????
=
1
3
, ∴CD=2AD, ∴
????
????
=
????
????
=
1
2
, 而∠A=∠C, ∴△AED∽△CBD.
24.【答案】解:(1)如图①,正方形E′F′P′N′即为所求. (2)设正方形E′F′P′N′的边长为x, ∵△ABC为正三角形, ∴AE′=BF′=
3
3
x. ∵E′F′+AE′+BF′=AB, ∴x+
3
3
x+
3
3
x=3+2
3
, ∴解得:x=3, 故答案为:3. ?/
25.【答案】解:
6
5
26.【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
27.【答案】(1)解:如图1, / 设正方形的边长为xmm,则PN=PQ=ED=x, ∴AE=AD-ED=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
??
120
=
80???
80
, 解得x=48. ∴加工成的正方形零件的边长是48mm (2)解:如图2, / 设PQ=x,则PN=2x,AE=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
2??
120
=
80???
80
, 解得: ??=
240
7
, ∴ 2??=
480
7
, ∴这个矩形零件的两条边长分别为
240
7
mm,
480
7
mm (3)解:如图3, / 设PN=x(mm),矩形PQMN的面积为S (??
??
2
) , 由条件可得 △??????~△?????? , ∴
????
????
=
????
????
, 即
??
120
=
80?????
80
, 解得: ????=80?
2
3
?? . 则 ??=?????????=??(80?
2
3
??)=?
2
3
??
2
+80??=?
2
3
(???60)
2
+2400 , 故S的最大值为 2400??
??
2
,此时 ????=60???? , ????=80?
2
3
×60=40(????)
【易错题解析】冀教版九年级数学上册 第25章 图形的相似 单元检测试卷
一、单选题(共10题;共30分)
1.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.?15m?????????????????????????????????/B.?60m?????????????????????????????????/C.?20m?????????????????????????????????/D.?10 /m
【答案】A
【考点】相似三角形的应用
【解析】【解答】设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得: /= /, ∴x= /=15 ∴这棵树的高度是15m. 故选A. 【分析】在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
2.如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ /= /?;④AB2=BD?BC . 其中一定能够判定△ABC是直角三角形的有( ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
【答案】B
【考点】相似三角形的判定与性质
【解析】解答:(1)∠B+∠DAC=90°,该条件无法判定△ABC是直角三角形;(2)∵∠B=∠DAC , ∠BAD+∠B=90°,∴∠BAD+∠DAC=90°,即∠BAC=90°,故该条件可以判定△ABC是直角三角形;(3) /= /,该条件无法判定△ABC是直角三角形;(4)∵AB2=BD?BC , ∴ /= /, ∵∠B=∠B , ∴△ABD∽△CBA , ∴∠BAC=90°,故该条件可以判定△ABC是直角三角形; 故选 B 分析:对题干中给出的条件逐一验证,证明∠BAC=90°即可解题.
3.线段MN长为1cm,点P是MN的黄金分割点,则MP的长是(?? )
A.?
5
?1
2
???????????????????????????/B.?
3?
5
2
???????????????????????????/C.?
5
?1
2
或
3?
5
2
???????????????????????????/D.?不能确定
【答案】C
【考点】黄金分割
【解析】【解答】解:设MP=x,则PN=1﹣x,根据题意得
??
1???
=
1???
1
, 解得,x=
3?
5
2
或
3+
5
2
>1(不合题意,舍去), 又因为题中没强调MP是长的一段还是短的一段,所以MP的长也可以为1﹣
3?
5
2
=
5
?1
2
. 故选C. 【分析】根据黄金分割点的概念,结合题目要求,列出方程求解即可.
4.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=
1
2
OD′,则A′B′∶AB为( ??) /
A.?2∶3????????????????????????????????????/B.?3∶2????????????????????????????????????/C.?1∶2????????????????????????????????????/D.?2∶1
【答案】D
【考点】位似变换
【解析】【解答】解:位似图形上任意一对对应点,到位似中心的距离之比都等于相似比. ∴A′B′:AB=OD′:OD=2:1. 故答案为:D. 【分析】由题,根据OD与OD′的数量关系,可以得出两个图形的位似比。
5.如图,l1∥l2∥l3 , 其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③
????
????
=
????
????
. 其中正确的有( )
/
A.?3个
???????????????????????????????????????B.?2个
???????????????????????????????????????C.?1个
???????????????????????????????????????D.?0个
【答案】A
【考点】相似三角形的判定与性质
【解析】【解答】解:l1与l2、l2与l3间的距离为l,则△ADE和△ABC分别是l,2l,
∵l1∥l2∥l3 ,
∴△ADE∽△ABC,
∴故选项②正确.
∵△ADE∽△ABC,
∴
????
????
=
????
????
,
∴故选项③正确,
∵△ADE∽△ABC,
????
????
=
1
21
=
1
2
,
即BC=2DE,
故正确的有3个,
故选:A.
【分析】根据l1∥l2∥l3判断△ADE∽△ABC,根据相似三角形的性质对所给命题进行判断.
6.如图,小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为(?? ) /
A.?10m??????????????????????????????????????/B.?9m??????????????????????????????????????/C.?8m??????????????????????????????????????/D.?7m
【答案】B
【考点】相似三角形的应用
【解析】【解答】解:因为竹竿和旗杆均垂直于地面,所以构成两个相似三角形, 若设旗杆高x米, 则
2.4
??
=
8
8+22
, ∴x=9. 故选B. 【分析】利用相似三角形对应边成比例解题.
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.?75cm,115cm???????????????/B.?60cm,100cm???????????????/C.?85cm,125cm???????????????/D.?45cm,85cm
【答案】A
【考点】相似三角形的性质
【解析】【解答】解:根据题意两个三角形的相似比是15:23,周长比就是15:23, 大小周长相差8份,所以每份的周长是40÷8=5cm, 所以两个三角形的周长分别为5×15=75cm,5×23=115cm.故选A. 【分析】根据题意两个三角形的相似比是15:23,可得周长比为15:23,计算出周长相差8份及每份的长,可得两三角形周长.
8.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM∶MC等于 (???? ) /
A.?1∶2????????????????????????????????????/B.?1∶3????????????????????????????????????/C.?1∶4????????????????????????????????????/D.?1∶5
【答案】B
【考点】三角形中位线定理,相似三角形的判定与性质
【解析】【分析】根据中位线定理证明△NDM∽△NBC后求解.
【解答】∵DE是△ABC的中位线,M是DE的中点, ∴DM∥BC,DM=ME=
1
4
BC. ∴△NDM∽△NBC,
????
????
=
????
????
=
1
4
. ∴
????
????
=
1
3
.
故选:B
【点评】本题考查了三角形中位线定理及相似三角形的性质.
9.如图,在△??????中,点??、??分别在????、????上,????//????,若????=4,????=2,则
????
????
的值为(???? ) /
A.?
1
2
??????????????????????????????????????????/B.?
2
3
??????????????????????????????????????????/C.?
3
4
??????????????????????????????????????????/D.?2
【答案】B
【考点】相似三角形的判定与性质
【解析】【分析】由????//????可证得△??????~△??????,再根据相似三角形的性质求解即可。 【解答】∵????//???? ∴△??????~△?????? ∵????=4,????=2 ∴
????
????
=
????
????
=
4
6
=
2
3
故选B。 【点评】相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握。
10.(2017?贵港)如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是
1
2
,其中正确结论的个数是(?? ) /
A.?2???????????????????????????????????????????/B.?3???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?5
【答案】D
【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
【解析】【解答】解:∵正方形ABCD中,CD=BC,∠BCD=90°, ∴∠BCN+∠DCN=90°, 又∵CN⊥DM, ∴∠CDM+∠DCN=90°, ∴∠BCN=∠CDM, 又∵∠CBN=∠DCM=90°, ∴△CNB≌△DMC(ASA),故①正确; 根据△CNB≌△DMC,可得CM=BN, 又∵∠OCM=∠OBN=45°,OC=OB, ∴△OCM≌△OBN(SAS), ∴OM=ON,∠COM=∠BON, ∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON, 又∵DO=CO, ∴△CON≌△DOM(SAS),故②正确; ∵∠BON+∠BOM=∠COM+∠BOM=90°, ∴∠MON=90°,即△MON是等腰直角三角形, 又∵△AOD是等腰直角三角形, ∴△OMN∽△OAD,故③正确; ∵AB=BC,CM=BN, ∴BM=AN, 又∵Rt△BMN中,BM2+BN2=MN2 , ∴AN2+CM2=MN2 , 故④正确; ∵△OCM≌△OBN, ∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1, ∴当△MNB的面积最大时,△MNO的面积最小, 设BN=x=CM,则BM=2﹣x, ∴△MNB的面积=
1
2
x(2﹣x)=﹣
1
2
x2+x, ∴当x=1时,△MNB的面积有最大值
1
2
, 此时S△OMN的最小值是1﹣
1
2
=
1
2
,故⑤正确; 综上所述,正确结论的个数是5个, 故选:D. / 【分析】根据正方形的性质,依次判定△CNB≌△DMC,△OCM≌△OBN,△CON≌△DOM,△OMN∽△OAD,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
二、填空题(共10题;共33分)
11.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD=10,BD=5,AE=6,则CE的长为________。/
【答案】3
【考点】平行线分线段成比例
【解析】【解答】根据平行线分线段成比例定理即由DE∥BC,可直接得
????
????
=
????
????
,即
10
5
=
6
????
,解得EC=3.【分析】运用平分线分线段成比例,列出比例等式求CE的长即可。
12.在某天的同一时刻,高为 1.5?? 的小明的影长为 1?? ,烟囱的影长为 20?? ,则这座烟囱的高为________ ?? .
【答案】30
【考点】平行线分线段成比例
【解析】【解答】解: 设烟囱的高为x, 由题意得:
1.5
1
=
??
20
,
∴x=30
∴烟囱的高为30米.
故答案为:30.
【分析】根据同一时刻,同一地点同一水平面上,不同物体的高度与影长成比例,即可列出方程,求解即可。
13.如图,在△ABC中,DE∥BC,
????
????
=
1
3
,则
????
????
=________. /
【答案】
1
3
【考点】相似三角形的判定与性质
【解析】【解答】解:∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C, ∴△ADE∽△ABC, ∴
????
????
=
????
????
=
1
3
. 故答案为:
1
3
【分析】根据相似三角形的对应边成比例求解。
14.为了测量校园里水平地面上的一棵大树的高度,数学综合实践活动小组的同学们开展如下活动:某一时刻,测得身高1.6m的小明在阳光下的影长是1.2m,在同一时刻测得这棵大树的影长是3.6m,则此树的高度是________m.
【答案】4.8
【考点】相似三角形的应用,平行投影
【解析】【解答】解:设此树的高度是hm,则
1.6
1.2
=
?
3.6
,解得h=4.8(m). 故答案为:4.8. 【分析】设此树的高度是hm,再根据同一时刻物高与影长成正比即可得出结论.
15.(2015?佛山市)如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10
2
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 ________. /
【答案】25
【考点】正方形的性质,相似三角形的判定与性质
【解析】【解答】∵在Rt△ABC中,AB2+BC2=AC2 , ∵AB=BC,AC=10
2
. ∴2AB2=200, ∴AB=BC=10, 设EF=x,则AF=10﹣x ∵EF∥BC, ∴△AFE∽△ABC ∴
????
????
=
????
????
,即
x
10
=
10???
10
, ∴x=5, ∴EF=5, ∴此正方形的面积为5×5=25. 故答案为25. 【点评】主要考查了正方形基本性质和比例线段的运用.解题的关键是准确的找到相似三角形并根据其相似比列方程求解.
16.一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.________?(判断对错)
【答案】×
【考点】相似三角形的性质
【解析】【解答】解:∵相似三角形的边长的比等于相似比,面积的比等于相似比的平方, ∴一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍,错误. 故答案为:×. 【分析】根据相似多边形的面积的比等于相似比的平方解答.
17.如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC=
10
,AC=5,那么△DBF的面积等于________. /
【答案】
45
16
【考点】相似三角形的性质,旋转的性质
【解析】【解答】解:∵△BDC∽△ABC, ∴
????
????
=
????
????
,∠CBD=∠A, ∴CD=
??
??
2
????
, ∵BC=
10
,AC=5, ∴CD=2, ∴AD=3, ∵将△ABC绕点B按逆时针方向旋转得到△EBD, / ∴∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC, ∴∠EBF=∠CBD, ∴∠EBF=∠A, ∴BE∥AC, ∴∠ADF=∠E, ∴∠E=∠EBF=∠A=∠ADF, ∴EF=BF,AF=DF, ∴AF+BF=EF+DF, 即AB=DE=AC=5, ∵AD∥BE, ∴△ADF∽△BEF, ∴
????
????
=
????
????
=
3
5
, ∴
????
????
=
3
8
, 过A 作AH⊥BC于H, ∴AH=
5
2
?
(
10
2
)
2
=
3
10
2
, ∵S△BDE=S△ABC=
1
2
×
10
×
3
10
2
=
15
2
, ∴△DBF的面积=
3
8
S△ABC=
45
16
. 故答案为:
45
16
. 【分析】根据相似三角形的性质得到
????
????
=
????
????
,∠CBD=∠A,得到CD=2,AD=3,根据旋转的性质得到∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,得到∠EBF=∠A,根据平行线的判定和性质得到∠ADF=∠E,等量代换得到∠E=∠EBF=∠A=∠ADF,根据等腰三角形的判定得到EF=BF,AF=DF,得到AB=DE=AC=5,根据相似三角形的性质得到
????
????
=
3
8
,过A 作AH⊥BC于H,于是得到结论.
18.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. /
【答案】(-10,3)
【考点】勾股定理,矩形的性质,翻折变换(折叠问题),相似三角形的判定与性质
【解析】【解答】解:∵矩形ABCO中, ∴CE∥AO. ∴△CEF∽△OFA. ∴
????
????
=
????
????
. 又∵OA=8,CF=4. ∴OF=2CE. 设CE=x,则BE=8-x. 根据折叠的性质,可得EF=8-x. ∴
??
2
+
4
2
=
(8???)
2
, ∴x=3, ∴OF=6, ∴OC=10, ∴点E的坐标为(-10,3). 故答案为:(-10,3) 【分析】根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得 x 2 + 4 2 = ( 8 ? x ) 2 ,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).
19.正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. (1)如图,若tanB=2,则
????
????
的值为________? (2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若
????′
????′
=
3
2
5
, 则tanB的值为________? /
【答案】
1
3
;
3
4
【考点】相似三角形的判定与性质
【解析】解:(1)∵四边形CEDF为正方形, ∴ED=EC,∠CED=90°, 在Rt△BDE中,∵tanB=
????
????
=2, ∴DE=2BE, ∴/ (2)连结DC、DC′,如图, ∵△ABC绕点D旋转得到△A′B′C′, ∴DB=DB′,DC=DC′,∠BDB′=∠CDC′, 即/ ∴△DBB′∽△DCC′, ∴
????
????
=
????′
????′
=
3
2
5
设DC=3
2
x,BD=5x, ∵四边形CEDF为正方形, ∴DE=3x, 在Rt△BDE中,BE=/ ∴tanB=/ 故答案为
1
3
,
3
4
. / 【分析】(1)由正方形的性质得ED=EC,∠CED=90°,再在Rt△BDE中,利用正切的定义得到DE=2BE,则CE=BE,所以
????
????
=
1
3
; ???????????? (2)连结DC、DC′,如图,根据旋转的性质得DB=DB′,DC=DC′,∠BDB′=∠CDC′,则可判断△DBB′∽△DCC′,根据相似三角形的性质得
????
????
=
????′
????′
=
3
2
5
, 则可设DC=3
2
x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
20.如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论: ①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC, 其中正确的序号是________. /
【答案】①②③④
【考点】全等三角形的判定与性质,相似三角形的判定与性质
【解析】【解答】解: / ⑴结论①正确.理由如下: ∵∠1=∠2,∠1+∠CMN=90°,∠2+∠6=90°, ∴∠6=∠CMN,又∵∠5=∠CMN, ∴∠5=∠6, ∴AM=AE=BF. 易知ADCN为正方形,△ABC为等腰直角三角形,∴AB=AC. 在△ACM与△ABF中, {
????=????
∠??????=∠??=45°
????=????
, ∴△ACM≌△ABF(SAS), ∴CM=AF; ⑵结论②正确.理由如下: ∵△ACM≌△ABF,???????????????????????????????? ∴∠2=∠4, ∵∠2+∠6=90°, ∴∠4+∠6=90°, ∴CE⊥AF; ⑶结论③正确.理由如下: 证法一:∵CE⊥AF, ∴∠ADC+∠AGC=180°, ∴A、D、C、G四点共圆, ∴∠7=∠2, ∵∠2=∠4, ∴∠7=∠4, 又∵∠DAH=∠B=45°, ∴△ABF∽△DAH; 证法二:∵CE⊥AF,∠1=∠2, ∴△ACF为等腰三角形,AC=CF,点G为AF中点. 在Rt△ANF中,点G为斜边AF中点, ∴NG=AG, ∴∠MNG=∠3, ∴∠DAG=∠CNG. 在△ADG与△NCG中, {
????=????
∠??????=∠??????
????=????
, ∴△ADG≌△NCG(SAS), ∴∠7=∠1, 又∵∠1=∠2=∠4, ∴∠7=∠4, 又∵∠DAH=∠B=45°, ∴△ABF∽△DAH; ⑷结论④正确.理由如下: 证法一:∵A、D、C、G四点共圆, ∴∠DGC=∠DAC=45°,∠DGA=∠DCA=45°, ∴∠DGC=∠DGA,即GD平分∠AGC. 证法二:∵AM=AE,CE⊥AF, ∴∠3=∠4,又∠2=∠4,∴∠3=∠2 则∠CGN=180°﹣∠1﹣90°﹣∠MNG=180°﹣∠1﹣90°﹣∠3=90°﹣∠1﹣∠2=45°. ∵△ADG≌△NCG, ∴∠DGA=∠CGN=45°=
1
2
∠AGC, ∴GD平分∠AGC. 综上所述,正确的结论是:①②③④,共4个. 故答案为:①②③④ 【分析】 结论①正确,证明△ACM≌△ABF即可;结论②正确,由△ACM≌△ABF得出∠2=∠4,进而得∠4+∠6=90°,即CE⊥AF,结论③正确,证法一:利用四点共圆;证法二:利用三角形全等;结论④正确,证法一:利用四点共圆,证法二:利用三角形全等。
三、解答题(共7题;共57分)
21.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积. /?
【答案】解答:由已知得,DG∥BC ∴△ADG∽△ABC , ∵AH⊥BC ∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) /= /, 即DG= /=50(m), ∴S矩形DEFG=DE×DG=2000(m2).
【考点】相似三角形的应用
【解析】【分析】由于四边形DEFG是矩形,即DG∥EF , 此时有∠ADG=∠B , ∠AGD=∠C , 所以△ADG∽△ABC , 利用相似三角形的性质求得线段DG的长,最后求得矩形的面积.
22.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . /?
【答案】解答:根据题意得出:QR∥ST , 则△PQR∽△PST , 故 /= /, ∵QS=45m,ST=90m,QR=60m, ∴ /= /, 解得:PQ=90(m), ∴河的宽度为90米.
【考点】相似三角形的应用
【解析】【分析】根据相似三角形的性质得出 /= /,进而代入求出即可.
23.如图,在正三角形ABC中,D,E分别在AC,AB上,且
????
????
=
1
3
, AE=EB.求证:△AED∽△CBD. ?/
【答案】证明:∵△ABC为正三角形, ∴∠A=∠C=60°,BC=AB, ∵AE=BE, ∴CB=2AE, ∵
????
????
=
1
3
, ∴CD=2AD, ∴
????
????
=
????
????
=
1
2
, 而∠A=∠C, ∴△AED∽△CBD.
【考点】相似三角形的判定
【解析】【分析】先根据等边三角形的性质得到∠A=∠C=60°,BC=AB,由AE=BE可得到CB=2AE,再由
????
????
=
1
3
得到CD=2AD,则
????
????
=
????
????
, 然后根据两边及其夹角法可得到结论.
24.已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上. (1)如图,在正三角形ABC及其内部,以点A为位似中心,画出正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不谢画法,但要保留画图痕迹); (2)若正三角形ABC的边长为3+2
3
, 则(1)中画出的正方形E′F′P′N′的边长 . ?/
【答案】解:(1)如图①,正方形E′F′P′N′即为所求. (2)设正方形E′F′P′N′的边长为x, ∵△ABC为正三角形, ∴AE′=BF′=
3
3
x. ∵E′F′+AE′+BF′=AB, ∴x+
3
3
x+
3
3
x=3+2
3
, ∴解得:x=3, 故答案为:3. ?/
【考点】位似变换
【解析】【分析】(1)利用位似图形的性质,作出正方形EFPN的位似正方形E′F′P′N′,如答图①所示; (2)根据正三角形、正方形、直角三角形相关线段之间的关系,利用等式E′F′+AE′+BF′=AB,列方程求得正方形E′F′P′N′的边长.
25.如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,且DAPQ=90°,AQ与BP相交于点T,则
????
????
的值为多少? /
【答案】解:
6
5
【考点】平行线的判定,勾股定理,正方形的性质,相似三角形的判定与性质
【解析】【解答】解 : 过点B作BE⊥AQ于点E,过点 P作PH⊥AQ于点H,?? / 设正方形的边长是2.则DP=CP=1,AD=2. ∴AP=
5
∵∠APQ=90°, ∴∠APD+∠CPQ=90° , 又∵∠APD+∠PAD=90° , ∴∠PAD=∠CPQ, ∵∠C=∠D ; ∴△ADP∽△PCQ. ∴AD:PC=AP:PQ=DP:CQ. 即2:1=
5
:PQ=1:CQ, 所以PQ=
5
2
, CQ=0.5. BQ=2?0.5=1.5. ∴AQ=
5
2
S△ABQ=
1
2
AB×BQ=
1
2
AQ×BE BE=
????·????
????
=
6
5
S△APQ=
1
2
AP×PQ=
1
2
AQ×PH, PH=
????·????
????
=1; 又BE⊥AQ,PH⊥AQ, ∴BE∥PH; ∴△BET∽△PHT, BT:PT=BE:PH=6:5. 【分析】 过点B作BE⊥AQ于点E,过点 P作PH⊥AQ于点H, 设正方形的边长是2.则DP=CP=1,AD=2.根据勾股定理得出AQ的长度,根据平角的定义,及直角三角形两锐角互余得出∠APD+∠CPQ=90°,∠APD+∠PAD=90°,根据同角的余角相等得出∠PAD=∠CPQ,从而判断出△ADP∽△PCQ.根据相似三角形对应边成比例得出AD:PC=AP:PQ=DP:CQ.从而得出PQ.CQ,BQ,AQ,的长度,根据面积法得出BE,PH的长度,根据垂直于同一直线的两条直线互相平行得出BE∥PH;根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似,得出△BET∽△PHT,根据相似三角形对应边的比等于对应高的比得出结论。
26.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
【考点】平行线分线段成比例
【解析】【分析】(1)由平行线分线段成比例得出比例式,即可得出结果; (2)先证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
27.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. /
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图 /,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
【答案】(1)解:如图1, / 设正方形的边长为xmm,则PN=PQ=ED=x, ∴AE=AD-ED=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
??
120
=
80???
80
, 解得x=48. ∴加工成的正方形零件的边长是48mm (2)解:如图2, / 设PQ=x,则PN=2x,AE=80-x, ∵ ????∥???? , ∴ △??????~△?????? , ∴
????
????
=
????
????
,即
2??
120
=
80???
80
, 解得: ??=
240
7
, ∴ 2??=
480
7
, ∴这个矩形零件的两条边长分别为
240
7
mm,
480
7
mm (3)解:如图3, / 设PN=x(mm),矩形PQMN的面积为S (??
??
2
) , 由条件可得 △??????~△?????? , ∴
????
????
=
????
????
, 即
??
120
=
80?????
80
, 解得: ????=80?
2
3
?? . 则 ??=?????????=??(80?
2
3
??)=?
2
3
??
2
+80??=?
2
3
(???60)
2
+2400 , 故S的最大值为 2400??
??
2
,此时 ????=60???? , ????=80?
2
3
×60=40(????)
【考点】相似三角形的判定与性质,配方法的应用
【解析】【分析】(1)设正方形的边长为x,则PN=PQ=ED=x,AE=AD-ED=80-x,由△APN ~ △ABC,根据相似三角形的性质可得
????
????
=
????
????
,代入可得x。 (2) 设PQ=x,则PN=2x,AE=80-x,由△APN~△ABC,根据相似三角形性质可得,
????
????
=
????
????
, 代入求得PQ,再求得PN。 (3) 根据相似三角形的性质可得
????
????
=
????
????
, 用含有x的代数式表示PQ,再表示面积S,最后配方求得S的最大值。
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
