3.6.3 二次函数的综合应用同步练习

第三章 二次函数
6 二次函数的应用
第3课时 二次函数的综合应用
课前预习
建立坐标系解决有关抛物线的问题
(1)建立__________________写出关键点的坐标。
(2)根据所建的坐标系设出_________________，列出____________,求出___________________。
(3)利用所求的关系式及其性质解决问题。
课内探究
探究要点1 建立坐标系解决实际问题
【例1】如图所示,有一座抛物线形涵洞,涵洞跨度AB=12m,内部高度h=4m.为了安全,汽车经过涵洞时,载货最高处与上方涵洞之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.以涵洞最高点为坐标原点O,以竖直方向为y轴建立平面直角坐标系,试运用二次函数的知识判断该车能否顺利通过。

思路分析:由如图所示的坐标系可知抛物线的顶点为(0,0),且A,B两点的坐标为(-6,-4),(6,-4),这样就求出了抛物线的表达式,再求抛物线上横坐标为-2或2时的点的纵坐标即可。
【自主解答】

交流分享
解决这类问题的关键是根据题意建立平面直角坐标系,数形结合,求出抛物线的表达式,从而进行解答。
跟踪练习
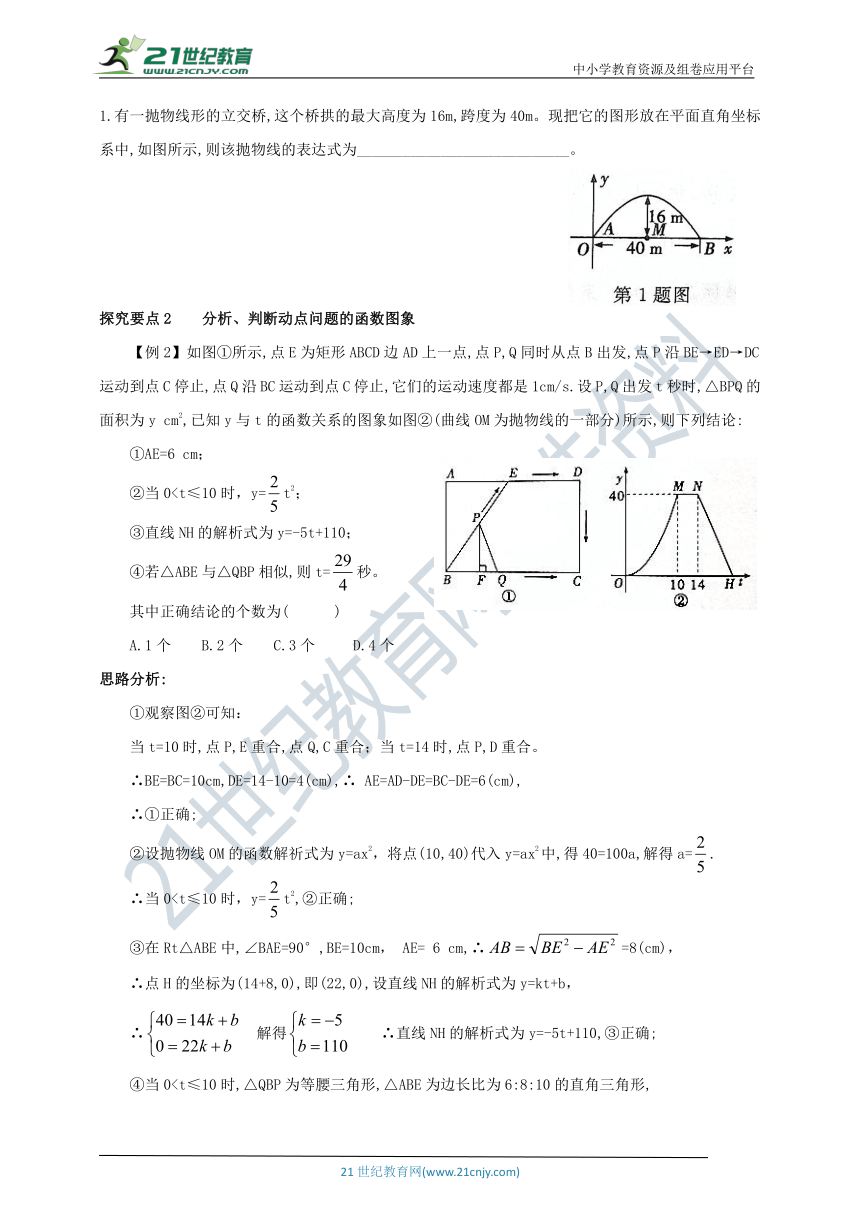
1.有一抛物线形的立交桥,这个桥拱的最大高度为16m,跨度为40m。现把它的图形放在平面直角坐标系中,如图所示,则该抛物线的表达式为____________________________。
探究要点2 分析、判断动点问题的函数图象
【例2】如图①所示,点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y cm2,已知y与t的函数关系的图象如图②(曲线OM为抛物线的一部分)所示,则下列结论:
①AE=6 cm；
②当0 ③直线NH的解析式为y=-5t+110；
④若△ABE与△QBP相似,则t=秒。
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
思路分析:
①观察图②可知：
当t=10时,点P,E重合,点Q,C重合；当t=14时,点P,D重合。
∴BE=BC=10cm,DE=14-10=4(cm),∴ AE=AD-DE=BC-DE=6(cm),
∴①正确;
②设抛物线OM的函数解祈式为y=ax2，将点(10,40)代入y=ax2中,得40=100a,解得a=.
∴当0 ③在Rt△ABE中,∠BAE=90°,BE=10cm， AE= 6 cm,∴=8(cm)，
∴点H的坐标为(14+8,0),即(22,0),设直线NH的解析式为y=kt+b，
∴ 解得 ∴直线NH的解析式为y=-5t+110,③正确;
④当0当t=秒时,△ABE与△QBP不相似,④不正确.
综上可知:正确的结论有3个. 答案:C
交流分享
本题考查了二次函数图象、待定系数法求函数友达式以及勾股定理,解题的关键是结合函数图象逐项分析4条结论是否成立,本题属于中档题,难度不大，解决该题型题目时,找出点的坐标,利用待定系数法求出函数表达式是关键。
跟踪练习
2.已知抛物线的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B,A作轴的垂线,垂足分别为C,D,连接PA,PD,PD交于点E,△PAD与△PEA相似吗?试说明理由。

课堂基础
一、选择题
1.如图①②所示,一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称,AB∥x轴,AB=4cm，最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线抛物线DFE的函数关系式为( )

A. B. C. D.
二、填空题
2.如图所示,某大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需___________秒。

3.如图所示是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面交于A,B两点,桥拱最高点C到直线AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m,则DE的长为______________m。
三、解答题
4.一座拱桥的轮廓是抛物线型(如图①所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m。
(1)将抛物线放在所给的直角坐标系中(如图②所示),其表达式是y=ax2+c形式,请根据所给数据求出a,c的值。
(2)求支柱MN的长度。
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车?请说明你的理由.(汽车间的间隔忽略不计)

四、拓展探究题
5.为纪念辛亥革命,某广告公司要设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x(米),面积为S(平方米)。
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围。
(2)请你设计一个方案,使获得的设计费最多并求出这个费用。
(3)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费用.(精确到1元,参考资料:①当矩形的长是宽与(长+宽)的比例中项时,这样的矩形叫做黄金矩形;
②≈2.236)

课后提升
1.顾老师在某次投篮中,球的运动路线是抛物线y=x2+3.5的一部分,如图所示,若球命中篮圈
中心,则他与篮圈底的距离是( )
A.4.6m B.4.5m C.4m D.3.5m

2.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
3.沙坪坝火车站将改造成一个集高开铁、轻轨、公交、停车场、商业于体的地下七层建筑,地面上欲建造一个圆形喷水池,如图所示,O点表示喷水池的水面中心,OA表示喷水柱子,水流从A点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用来描述,那么水池的半径至少要____________米,才能使喷出的水流不致落到池外。
4.2016年上半年,某种农产品受不良炒作的影响,价格一路上涨,8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至12月份,月平均价格y元/千克与月份x呈二次函数关系,已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克。
(1)分别求出当1≤x≤7和7≤x≤12时,y关于x的函数关系式。
(2)2016年的12个月中.这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有
哪些?
参考答案及解析
课前预习
(1)平面直角坐标系 (2)二次函数表达式 方程(组) 二次函数表达式
课内探究
【例1】由题意可知,抛物线的顶点为(0,0),A(-6,-4),B(6,-4),设抛物线的表达式为y=ax2,将A(-6,-4)代入y=ax2得-4=a×(-6)2,∴a=∴y=x2.∵卡车宽为4m,
∴当x=2时,y=- ×22= ,∴EF=4- =3(m), ∴CE=EF-CF=3-2.5=Cm).>0.5,∴该车能顺利通过。
跟踪练习
1.
2.解:相似.理由如下:令x=0,则y=1, OP= 1。
设点A的横坐标为m,则AD=-m2+1.∵AB⊥y轴,AD⊥x轴,
∴AF=OD=m,OF=-m2+1,PF=1-(-m2+1)=m2
在Rt△PAF中,PA2=PF2+AF2=(m2)2+m2=m4+m2,
在R△POD中,,
由AB∥x轴,得△PEF∽△PDO, ∴ 解得,。∴PA2=PD· PE=m4+m2
∵∠APE=∠DPA
∴△PAD∽△PEA.
课堂基础
1.C 2.36 3.48
4.解:(1)根据题目条件,A,B,C的坐标分别是(-10,0),(10,0),(0,6),将B,C的坐标代入y=ax2+c,得 解得 所以抛物线的表达式是y=x2+6.
(2)可设N(5,yN),于是yN=，支柱MN的长度是10-4.5=5.5(m)
(3)设DE是隔离带的宽,EG是三辆汽车的宽度和,则G点坐标是(7,0),
过G点作GH⊥AB,交抛物线于点H,如图所示,则。
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车。
5.解:(1)因为矩形的周长为12米,其中一边长为x米,所以S=x(6-x)=-x2+6x,自变量x的取值范围是0 (2)因为S=-x2+6x=-(x-3)2+9,所以当x=3时,S最大为9,此时广告费用最多,即矩形广告牌设计成边长为3米的正方形时,面积最大,最大面积为9平方米,此时可获得的最多设计费用为
9×1000=9000(元)。
(3)设黄金矩形的长为a米,宽为b米根据题意,得 解得
或 （舍去）
即当矩形长为(3-3)米时,将成为黄金矩形。 所以S=ab=(3-3)(9-3)=36(-2)≈8.496(m2)。可获得设计费约为8.496×1000=8496(元)。
课后提升
1.B 2.C
3.3.5 解析:根据题意可得出,当y=0时,则0=,整理,得4x2-12x-7=0,解得x1=-0.5,x2=3.5.∴水池的半径至少要3.5米,才能使喷出的水流不致落到池外。
4.解:(1)当1≤x≤7时,设y=kx+m 。将点(1,8),(7,26)分别代入,得,解得
∴当1≤x≤7时,函数关系式为y=3x+5。
当7≤x≤12时,设y=ax2+bx+c. 将(7,26),(9,14),(12,11)分别代入, 得
解得 ∴当7≤x≤12时,函数关系式为y=x2-22x+131.
(2)当1≤x≤7时,y=3x+5为增函数，当x=1时,y最小值=8。
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,当x=11时,y最小值=10。
∴该农产品月平均价格最低的是1月,最低为8元/千克。
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值。
将x=8和x=10代入y=x2-22x+131得y=19和y=11,∴后5个月的月平均价格分别为19,14,11,10,11.
∴年平均价格为(元/千克)。
当x=3时,y=14<15.3,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格。