沪科版九年级数学上册第21章二次函数与反比例函数单元检测试卷含答案
文档属性
| 名称 | 沪科版九年级数学上册第21章二次函数与反比例函数单元检测试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 100.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-14 18:36:57 | ||
图片预览



文档简介
沪科版九年级数学上册 第21章 二次函数与反比例函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知函数,当时,函数值等于,则的值是( )
A. B. C. D.任意实数
?2.已知点是双曲线上一点,则下列各点中在该图象上的点是( )
A. B. C. D.
?3.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在位置时,水面宽度为,此时水面到桥拱的距离是,则抛物线的函数关系式为( )
A. B.
C. D.
?4.一次函数与反比例函数的图象的交点的情况为( )
A.只有一个交点 B.有两个交点
C.没有交点 D.不能确定
?5.如图,反比例函数的图象经过点,则此反比例函数的解析式为( )
A. B. C. D.
?6.抛物线的对称轴是直线( )
A. B. C. D.
?
7.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数)
C.(为整数) D.(为正整数)
?
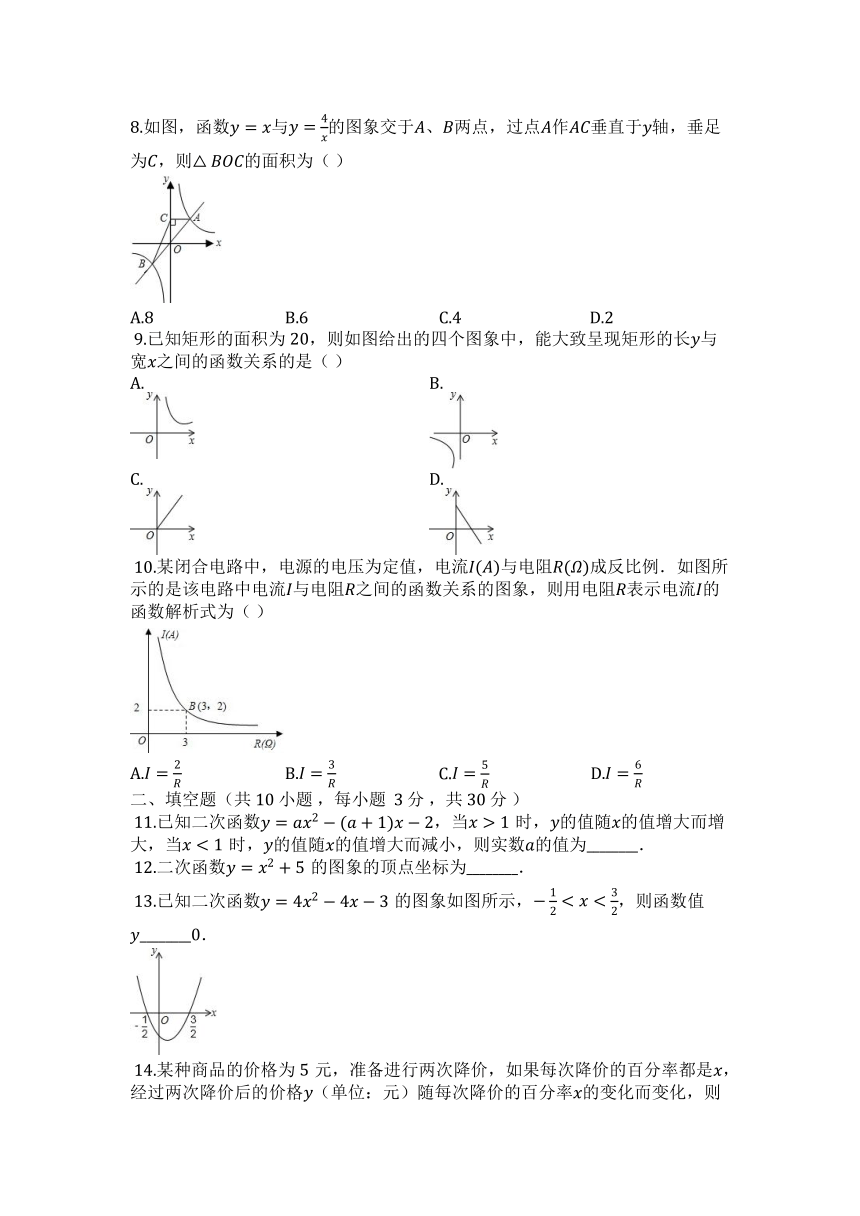
8.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为( )
A. B. C. D.
?9.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形的长与宽之间的函数关系的是( )
A. B.
C. D.
?10.某闭合电路中,电源的电压为定值,电流与电阻成反比例.如图所示的是该电路中电流与电阻之间的函数关系的图象,则用电阻表示电流的函数解析式为( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知二次函数,当时,的值随的值增大而增大,当时,的值随的值增大而减小,则实数的值为________.
?12.二次函数的图象的顶点坐标为________.
?13.已知二次函数的图象如图所示,,则函数值________.
?14.某种商品的价格为元,准备进行两次降价,如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则与之间的关系式为________.
?15.函数的自变量的取值范围是________.?
16.物体自由下落时,它所经过的距离(米)和时间(秒)之间可以用关系式来描述.建于年的上海金茂大厦高米,当时排名世界第三高楼.若从高米的观光厅上掉下一个物体,自由下落到地面约需________秒(精确到秒).?
17.二次函数图象的顶点坐标为________.?
18.当时,反比例函数的值为,则________.?
19.函数的图象与轴有且只有一个交点,那么的值和交点坐标分别为________.?
20.如图所示,矩形中,,,是线段上一点(不与重合),是上一点,且,设,的面积为,则与之间的函数关系式为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.已知反比例函数经过点.
求的值;
画出这个函数的图象;
在该函数的图象中,当时,随的增大而________.
?
22.如图,已知?,是一次函数的图象和反比例函的图象的交点.
求反比例函数的解析式;
求一次函数的解析式.
求的面积.
?
23.进价为每件元的某商品,售价为每件元时,每星期可卖出件,市场调查反映:如果每件的售价每降价元,每星期可多卖出件,但售价不能低于每件元,且每星期至少要销售件.设每件降价元?(为正整数),每星期的利润为元.
求与的函数关系式并写出自变量的取值范围;
若某星期的利润为元,此利润是否是该星期的最大利润?说明理由.
直接写出售价为多少时,每星期的利润不低于元?
?
24.某企业设计了一款工艺品,每件的成本是元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每天的销售量是件,而销售单价每降低元,每天就可多售出件,但要求销售单价不得低于成本
求每天的销售利润(元)与销售单价(元)之间的函数关系式;
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
?
25.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线的对称轴是且经过、两点,与轴的另一交点为点,连结.
填空:点、点和点的坐标分别为________,________,________;
求证:;
求抛物线解析式;
若点为直线上方的抛物线上的一点,连结,,求面积的最大值,并求出此时点的坐标.
?
26.中秋节期间某水库养殖场为适应市场需求,连续用天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第天(且为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元)
单位捕捞成本(元)
捕捞量
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
求第天的收入(元)与(天)之间的函数关系式?(当天收入日销售额-日捕捞成本)
在第几天取得最大值,最大值是多少?
答案
1.A
2.B
3.C
4.C
5.C
6.A
7.A
8.D
9.A
10.D
11.
12.
13.
14.
15.全体实数
16.
17.
18.
19.,;,;,;
20.
21.减小.
22.解:将,两点坐标代入中,
得,
解得,,
∴反比例函数解析式为;将,代入中,得,
解得,
∴一次函数的解祈式为;
设直线交轴于点,
由直线的解析式得,
∴.
23.解:依题意,得,
∵,
∴;(2),
∵,
∴不是最大利润.当时,,
解得,,
故当时,,
即当售价在不小于元且不大于元时,月利润不低于元.
24.解:(1)
所以;(2)
∵,
∴抛物线开口向下.
∵,对称轴是直线,
∴当时,;
即销售单价为元时,每天的销售利润最大,最大利润是元.
25.∵,,,
∴,,,
∴,,
∴,
又∵,
∴;∵抛物线过,,
∴可设抛物线解析式为,
又∵抛物线过点,
∴
∴,
∴.设.
过点作轴交于点,
∴,
∴
,
∵,
,
∴当时,的面积有最大值是,
此时.
26.解:由题意,得
;∵,,
又∵且为整数,
∴当时,随的增大而增大;
当时,随的增大而减小;
当时即在第天,取得最大值,最大值为.
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知函数,当时,函数值等于,则的值是( )
A. B. C. D.任意实数
?2.已知点是双曲线上一点,则下列各点中在该图象上的点是( )
A. B. C. D.
?3.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在位置时,水面宽度为,此时水面到桥拱的距离是,则抛物线的函数关系式为( )
A. B.
C. D.
?4.一次函数与反比例函数的图象的交点的情况为( )
A.只有一个交点 B.有两个交点
C.没有交点 D.不能确定
?5.如图,反比例函数的图象经过点,则此反比例函数的解析式为( )
A. B. C. D.
?6.抛物线的对称轴是直线( )
A. B. C. D.
?
7.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数)
C.(为整数) D.(为正整数)
?
8.如图,函数与的图象交于、两点,过点作垂直于轴,垂足为,则的面积为( )
A. B. C. D.
?9.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形的长与宽之间的函数关系的是( )
A. B.
C. D.
?10.某闭合电路中,电源的电压为定值,电流与电阻成反比例.如图所示的是该电路中电流与电阻之间的函数关系的图象,则用电阻表示电流的函数解析式为( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知二次函数,当时,的值随的值增大而增大,当时,的值随的值增大而减小,则实数的值为________.
?12.二次函数的图象的顶点坐标为________.
?13.已知二次函数的图象如图所示,,则函数值________.
?14.某种商品的价格为元,准备进行两次降价,如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则与之间的关系式为________.
?15.函数的自变量的取值范围是________.?
16.物体自由下落时,它所经过的距离(米)和时间(秒)之间可以用关系式来描述.建于年的上海金茂大厦高米,当时排名世界第三高楼.若从高米的观光厅上掉下一个物体,自由下落到地面约需________秒(精确到秒).?
17.二次函数图象的顶点坐标为________.?
18.当时,反比例函数的值为,则________.?
19.函数的图象与轴有且只有一个交点,那么的值和交点坐标分别为________.?
20.如图所示,矩形中,,,是线段上一点(不与重合),是上一点,且,设,的面积为,则与之间的函数关系式为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.已知反比例函数经过点.
求的值;
画出这个函数的图象;
在该函数的图象中,当时,随的增大而________.
?
22.如图,已知?,是一次函数的图象和反比例函的图象的交点.
求反比例函数的解析式;
求一次函数的解析式.
求的面积.
?
23.进价为每件元的某商品,售价为每件元时,每星期可卖出件,市场调查反映:如果每件的售价每降价元,每星期可多卖出件,但售价不能低于每件元,且每星期至少要销售件.设每件降价元?(为正整数),每星期的利润为元.
求与的函数关系式并写出自变量的取值范围;
若某星期的利润为元,此利润是否是该星期的最大利润?说明理由.
直接写出售价为多少时,每星期的利润不低于元?
?
24.某企业设计了一款工艺品,每件的成本是元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每天的销售量是件,而销售单价每降低元,每天就可多售出件,但要求销售单价不得低于成本
求每天的销售利润(元)与销售单价(元)之间的函数关系式;
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
?
25.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线的对称轴是且经过、两点,与轴的另一交点为点,连结.
填空:点、点和点的坐标分别为________,________,________;
求证:;
求抛物线解析式;
若点为直线上方的抛物线上的一点,连结,,求面积的最大值,并求出此时点的坐标.
?
26.中秋节期间某水库养殖场为适应市场需求,连续用天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第天(且为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元)
单位捕捞成本(元)
捕捞量
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
求第天的收入(元)与(天)之间的函数关系式?(当天收入日销售额-日捕捞成本)
在第几天取得最大值,最大值是多少?
答案
1.A
2.B
3.C
4.C
5.C
6.A
7.A
8.D
9.A
10.D
11.
12.
13.
14.
15.全体实数
16.
17.
18.
19.,;,;,;
20.
21.减小.
22.解:将,两点坐标代入中,
得,
解得,,
∴反比例函数解析式为;将,代入中,得,
解得,
∴一次函数的解祈式为;
设直线交轴于点,
由直线的解析式得,
∴.
23.解:依题意,得,
∵,
∴;(2),
∵,
∴不是最大利润.当时,,
解得,,
故当时,,
即当售价在不小于元且不大于元时,月利润不低于元.
24.解:(1)
所以;(2)
∵,
∴抛物线开口向下.
∵,对称轴是直线,
∴当时,;
即销售单价为元时,每天的销售利润最大,最大利润是元.
25.∵,,,
∴,,,
∴,,
∴,
又∵,
∴;∵抛物线过,,
∴可设抛物线解析式为,
又∵抛物线过点,
∴
∴,
∴.设.
过点作轴交于点,
∴,
∴
,
∵,
,
∴当时,的面积有最大值是,
此时.
26.解:由题意,得
;∵,,
又∵且为整数,
∴当时,随的增大而增大;
当时,随的增大而减小;
当时即在第天,取得最大值,最大值为.
